1. 引言
1.1. 研究背景
迄今为止,在很多学术领域上都存在着大量各类型非线性方程待求解的问题。然而,这类方程往往难以得到精确解,于是非线性方程的精确求解及解法研究成了非线性科学中的前沿研究课题和热点问题。先前,已经有不少专家学者在研究如何求解非线性方程的精确解方面做了大量有效的工作,构造出多种有效的求解方法,如变分法,截断展开法,齐次平衡法 [1] [2] ,F展开法 [3] ,Jacobi椭圆函数展开法 [4] ,Lie群方法等。而非线性波动方程作为非线性方程的一个重要分支,其孤立波的特殊性质和求解方法也成为了研究的热点。由于求解非线性波动方程没有也不可能有统一而普遍适用的方法,所以需要尝试一些独立可行而有效的办法。
1895年,荷兰的特韦格教授(Korteweg)和他的学生de Vries,在长近似波和小振幅的假设下,建立了单向浅水波的数学模型,从而得到了经典KDV Equation
 。
。
本文研究的是如下KDV型方程的精确解:
 。(1.1)
。(1.1)
方程(1.1)在量子场论、等离子物理和固态物理中有着广泛的应用。
1.2. 本文研究的主要内容
本文利用行波约化的方法来探索方程(1.1)的精确解,主要思路是首先通过变量替换,将非线性偏微分方程转化为常微分方程,然后求解所得到的常微分方程。在求解常微分方程时通常有两种方法,一是
采用具体函数展开:如( )-展开法 [5] [6] [7] 。二是采用截断展开求解非线性方程,如本文用到的Exp-
)-展开法 [5] [6] [7] 。二是采用截断展开求解非线性方程,如本文用到的Exp-
函数方法。再结合使用计算机符号运算系统Mathematica求解代数方程组,从而得到方程的各种精确解。
本文的内容安排如下:第二节介绍指数函数展开法在行波约化中的主要思想。第三节通过利用行波约化方法研究方程(1.1)得到了4种指数函数形式的解,并画出对应的图像,观察波的传播状况。最后一节是对本文内容的总结。
2. 方法概述
本节以如下的非线性偏微分方程
 (2.1)
(2.1)
为例来阐述一下Exp-函数展开法在行波约化中的应用方法,详细内容参考 [8] 。在方程(2.1)中,P为其变元的多项式,并包含非线性项和高阶偏导项,该方法的实施可分为以下几步:
1) 首先进行行波约化,假设方程(2.1)具有行波解:
 ,其中
,其中
则方程(2.1)转化为自变量为η的非线性常微分方程
 (2.2)
(2.2)
2) 利用指数函数展开法求解非线性方程,假设(2.2)的方程具有如下形式:
 (2.3)
(2.3)
其中c,d,p和q为待定正整数, 和
和 为待定常数。
为待定常数。
3) 将(2.3)代入到(2.2)中,然后平衡(2.2)中的非线性项和最高阶导数项的最高次数可以得到p和c的关系。同理,平衡非线性项和最高阶导数项的最低次数可以得到q和d的关系。
4) 对c,d,p和q赋特殊值,并将(2.3)代入(2.2)中可以得到关于 的方程组。之后,令
的方程组。之后,令 的系数为零,可得到一系列关于
的系数为零,可得到一系列关于 和
和 的代数方程,求解这些代数方程并将结果代入(2.3)中,即可求得(2.1)的解。
的代数方程,求解这些代数方程并将结果代入(2.3)中,即可求得(2.1)的解。
3. 方程(1.1)求解
本节利用上述的Exp-函数方法来求解方程(1.1)。对于该方程,把 代入到方程(1.1)中,可得
代入到方程(1.1)中,可得
 (3.1)
(3.1)
假设方程(3.1)具有(2.3)形式的解,即:
 (3.2)
(3.2)
为了确定c和p之间的关系,将(3.2)代入(3.1)后计算可得


平衡 和
和 的最高次数可得
的最高次数可得 。同理,通过平衡
。同理,通过平衡 和
和 的最低次数可得
的最低次数可得 。特别的,令
。特别的,令 ,
, 此时,方程(3.2)可表示为
此时,方程(3.2)可表示为
 (3.3)
(3.3)
然后将(3.3)代入到方程(1.1)中,然后令 的系数为零,即得关于待定系数
的系数为零,即得关于待定系数 的代数方程组,借助Mathematica软件求解这个方程组,得到如下几种情形的解。
的代数方程组,借助Mathematica软件求解这个方程组,得到如下几种情形的解。
情形1:得到如下形式的解

其中,取 ,
, ,此时方程的解简化为
,此时方程的解简化为 ,其情形见图1。
,其情形见图1。
情形2:得到如下形式的解

特别的,当 ,
,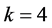 ,方程的解简化为
,方程的解简化为 ,其情形见图2。
,其情形见图2。
情形3:得到如下形式的解

其中取 ,
, ,
, ,此时方程的解简化为
,此时方程的解简化为 ,其情形见图3。
,其情形见图3。
情形4:含有虚数的解

化简后展开得

特别的,当 ,方程的解化简为
,方程的解化简为 ,其情形见图4~6,分别为其实部、虚部、绝对值图像。
,其情形见图4~6,分别为其实部、虚部、绝对值图像。

Figure 4. The real part of solution for Case 4
图4. 情形4的解的实数部分

Figure 5. The imaginary part of solution for Case 4
图5. 情形4的解的虚数部分

Figure 6. The absolute value of solution for Case 4
图6. 情形4的解的绝对值
4. 总结
本文利用指数函数方法深入系统的分析了KDV型方程(1.1)的精确解,给出新的指数函数形式解,这些解能够加深对该方程的理解,从而促进该方程在物理学等领域中的分析应用,因此本文的工作具有一定的理论意义和应用价值。
致 谢
本文得到北方工业大学大学生科技活动项目、北方工业大学青年拔尖人才项目(XN071009)和优秀青年教师计划(XN132)支持。感谢项目指导教师张智勇老师的悉心指导。