1. 引言
在流体动力学中对流项的计算有着重要的意义。数值格式离散对流项时关系到数值结果的精度、稳定性和收敛性。因此,在计算流体力学中构造易于实现且能避免数值耗散的数值方法,仍然是一项具有挑战性和吸引力的研究目标。
目前已经有很多经典的格式,如一阶迎风格式FOU (First-order Upwind)和Lax-friedrichs格式 [1] 等。但这些格式大多都是低阶的,会产生较大的数值耗散。于是,人们又提出了一些格式,如中心差分格式CD (Central Difference)、二阶迎风格式SOU (Second-order Upwind)、Quick (Quadratic Upstream Interpolation for ConvectiveKinematics) [2] 格式和CUI (Cubic Upwind Interpolation) [3] 格式等。这些线性高阶格式的数值耗散较低,但是不满足对流有界性,数值解在间断解处会出现非物理震荡。
为了解决上述的问题,人们提出了高分辨率格式(High Resolution Scheme) [4] [5] ,它是高阶格式和某些有界性准则的结合。高分辨率格式最早是利用Harten提出的TVD (Total Variational Diminishing Constraint) [4] 性质构造一个限制器函数,然后将它和高阶格式结合构造出高分辨率格式。另外的一些重要的有界性准则包括Leonard提出的NVF (Normalized Variable Formulation) [6] 与Gaskell和Lau [1] 提出来的CBC (Convection Boundedness Criterion)准则等。在此基础上,构造出了一些对流有界格式,如SMART [7] ,CLAM [8] ,HOAB [9] ,CUBISTA [10] 等。
本文以CUI格式为基础,构造了一个满足对流有界性的一个无振荡格式mCUI。本文的具体安排如下:第二节建立对流项的高分辨率格式,第三节给出经典的算例及讨论计算结果,第四节给出结论。
2. 建立数值格式
2.1. 高阶格式
以图1所示,数值格式在离散对流项的时候,一般会用到该界面值相邻三个点
由此常见线性格式可统一表示为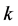 格式
格式
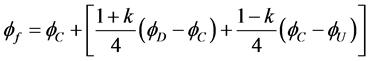 (1)
(1)
其中,参数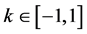 ,对
,对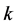 赋不同的值可以得到不同的高阶格式。根据Leonard [11] 的正则化思想,正则化变量定义为
赋不同的值可以得到不同的高阶格式。根据Leonard [11] 的正则化思想,正则化变量定义为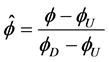 ,则
,则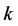 格式(1)可以化为
格式(1)可以化为
 (2)
(2)
由式(2)得知, 的变化只依赖于
的变化只依赖于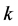 和
和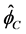 。表1给出了几种常见的对流格式的NV线。值得注意的是,这些线性高阶格式都不满足有界性,因此,采用有界性准则结合线性高阶格式来构造高分辨率格式。
。表1给出了几种常见的对流格式的NV线。值得注意的是,这些线性高阶格式都不满足有界性,因此,采用有界性准则结合线性高阶格式来构造高分辨率格式。
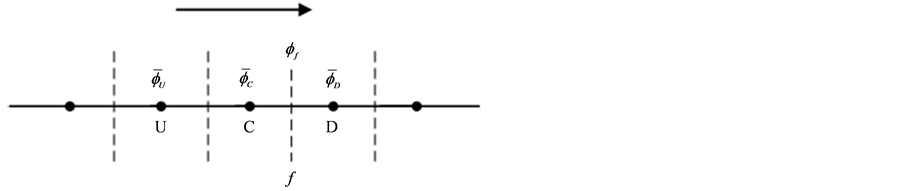
Figure 1. Three neighboring mesh points and the mesh face
图1. 三个相邻的节点及单元边界

Table 1. The linear convection schemes and the NV formulations
表1. 线性对流格式及其NV格式
在Leonard提出的NVD的基础上,利用正则化思想,CBC准则可以表达为
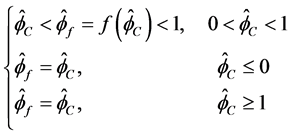
之后,Wei [9] 和Hou [12] 证明了CBC准则只能保证数值格式的有界性,不能保证数值格式的精度。为了克服这个缺点,Wei和Hou提出了一个改进的CBC准则即BAIR准则
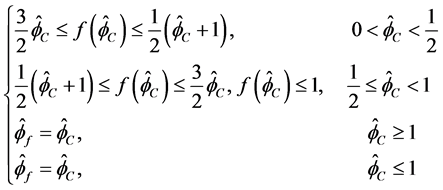
另外,TVD性质的正则化形式为
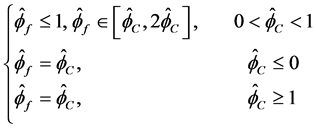
将BAIR区域与TVD区域绘制于图2中,阴影区域表示BAIR区域与TVD区域重合区域。正则化于是,只要格式的NV线落在阴影区域内,则格式同时满足BAIR条件和TVD条件,它将具备对流有界性 [9] [12] 。
2.2. 对流项的离散
由上可知,若格式满足对流有界性,那么格式的NV线必须落在TVD区域和BAIR区域的重合区域内。由前面提到的HR格式的标准化形式: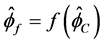 。由图2可知
。由图2可知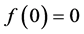 ,
,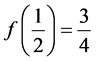 ,
,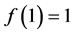 。由于所选取的CUI格式不满足对流有界性,因此利用分段的思想来构造mCUI格式,使得此格式满有足对流界性准则。在
。由于所选取的CUI格式不满足对流有界性,因此利用分段的思想来构造mCUI格式,使得此格式满有足对流界性准则。在 的区间内,选取原有的CUI格式,在
的区间内,选取原有的CUI格式,在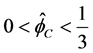 内,选取
内,选取 ,
, 和
和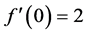 ,利用Hermite插值构造曲线,使其满足对流有界性;同理在
,利用Hermite插值构造曲线,使其满足对流有界性;同理在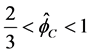 内,选取
内,选取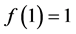 ,
,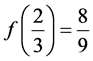 和
和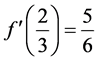 构造曲线,使曲线在重合的区域内。得到图3所示的满足对流有界性的格式mCUI格式。该格式的正则化形式为
构造曲线,使曲线在重合的区域内。得到图3所示的满足对流有界性的格式mCUI格式。该格式的正则化形式为

2.3. 时间离散
完成了关于空间项的离散后,得到了关于时间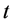 的一个常微分方程,即
的一个常微分方程,即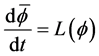 。为了避免非物理震荡,采用的是三阶TVDRunge-Kutta [13] 格式来离散时间,它的形式为
。为了避免非物理震荡,采用的是三阶TVDRunge-Kutta [13] 格式来离散时间,它的形式为
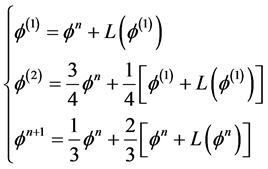
3. 数值结果及讨论
3.1. 一维线性对流方程
一维线性对流方程
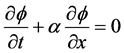 ,
,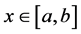 ,
, (3)
(3)
给定初值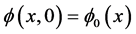 ,
,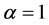 。
。
3.1.1. 情形1
首先给定以下的初值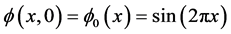 ,在区间
,在区间 上求解方程(3),
上求解方程(3),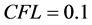 ,通过计算
,通过计算
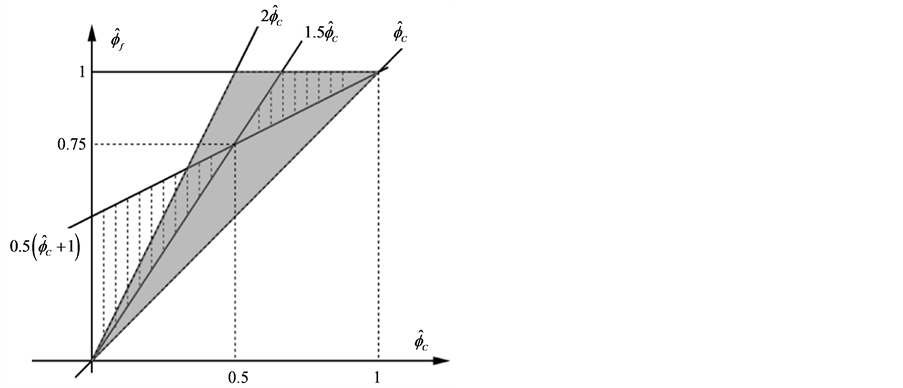
Figure 2. The regions of the TVD (shaded) and BAIR (hatched)
图2. BAIR区域(虚线部分)和TVD区域(阴影部分)
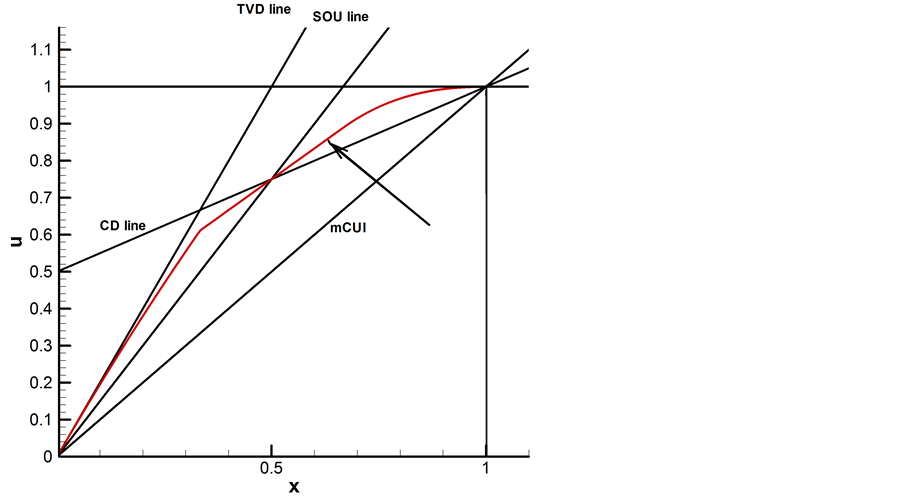
Figure 3. The illustration of the NV line of the mCUI scheme in the BAIR region
图3. mCUI格式在BAIR区域中的NV线
mCUI格式、SMART [7] 格式、MUSCL [14] 格式在等距剖分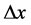 下的数值解,
下的数值解, 分别取20、40、80、160、320。计算格式的
分别取20、40、80、160、320。计算格式的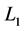 误差、
误差、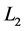 误差,同时算出数值精度阶(如表2),计算公式如下
误差,同时算出数值精度阶(如表2),计算公式如下
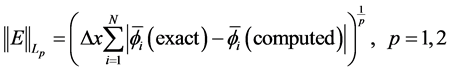
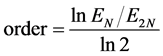
由表2可知,对于光滑解问题,mCUI格式可以达到理论上高阶精度。

Table 2. Errors and orders for several selected schemes
表2. 格式误差与数值精度阶对比
3.1.2. 情形2
对于上述的方程,再选取以下的间断初值
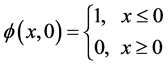 ,
,
计算区间为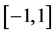 ,等分为800等份,计算时间T为0.1,图4表明,mCUI格式对间断解的计算有很好的逼近效果。
,等分为800等份,计算时间T为0.1,图4表明,mCUI格式对间断解的计算有很好的逼近效果。
3.1.3. 情形3
对于上述的方程,选取初值为如下的非光滑初值
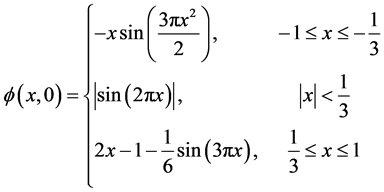
计算区间选为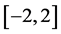 ,
, ,计算时间为
,计算时间为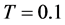 ,
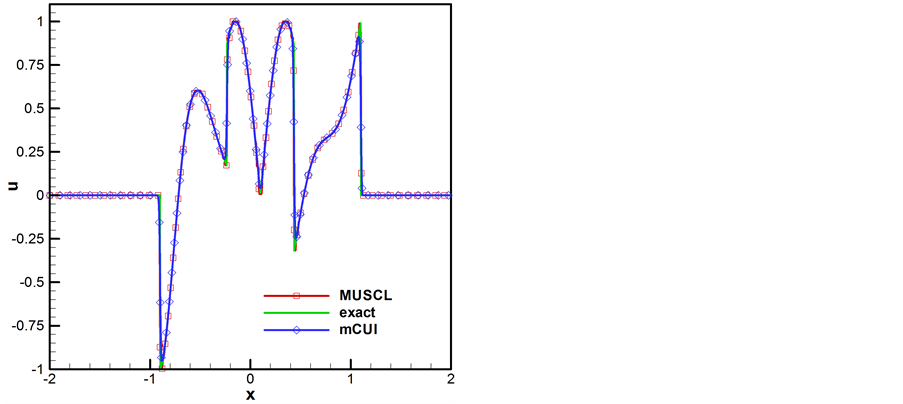
,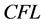 分别取为0.1和0.5得到图5(a)和图5(b),且把mCUI格式的结果和经典格式MUSCL的结果在同样条件下进行对比。通过对比,我们发现mCUI格式与经典CBC格式具有相同的逼近效果。
分别取为0.1和0.5得到图5(a)和图5(b),且把mCUI格式的结果和经典格式MUSCL的结果在同样条件下进行对比。通过对比,我们发现mCUI格式与经典CBC格式具有相同的逼近效果。
3.2. 一维非线性Burgers方程
一维的非线性Burgers方程的表达形式为
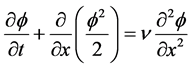 ,
,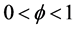 ,
,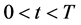 (4)
(4)
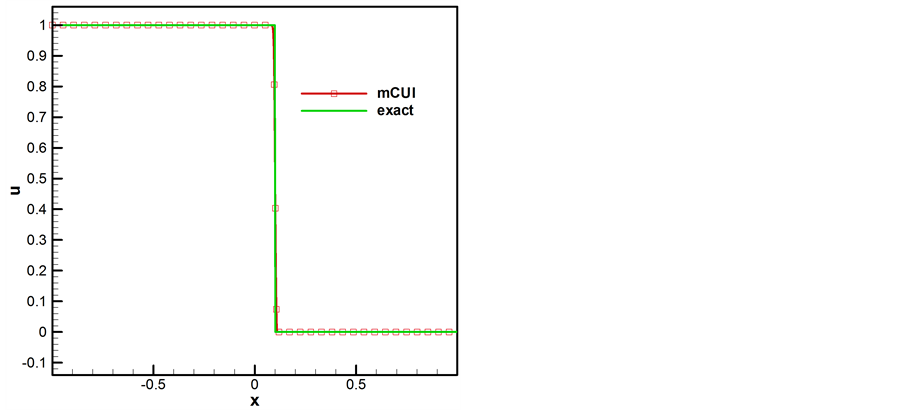
Figure 4. Comparison of numerical and exact results for the discontinuous initial condition
图4. mCUI格式的数值解和精确解

(a) (b)
(b)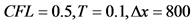
Figure 5.Comparison of MUSCL and mCUI scheme for the linear equation with nonsmooth initial distribution
图5. 非光滑初值下,MUSCL与mCUI的对比
其中 为粘性系数。当
为粘性系数。当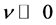 时,方程有光滑解,当
时,方程有光滑解,当 时,方程的解会随着时间出现间断。
时,方程的解会随着时间出现间断。
3.2.1. 情形1
选取区间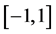 ,给定初值
,给定初值
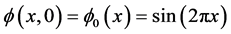
和边界条件

在给定的粘性系数下,上述的初始条件会随着时间的变化形成间断。
给定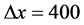 ,图6给出在不同的粘性系数下,随着时间的增加,最初的正弦波的变化,我们选取n = 0.1,0.01,0.001和0.0001,时间t = 0.0,0.1,0.2,0.3,0.4和0.5。
,图6给出在不同的粘性系数下,随着时间的增加,最初的正弦波的变化,我们选取n = 0.1,0.01,0.001和0.0001,时间t = 0.0,0.1,0.2,0.3,0.4和0.5。
3.2.2. 情形2
令 ,即对于无粘Burgers方程,选取以下的初值
,即对于无粘Burgers方程,选取以下的初值

这个问题的精确解是
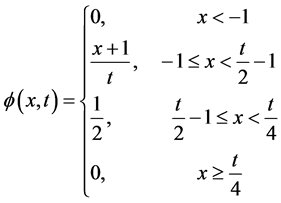
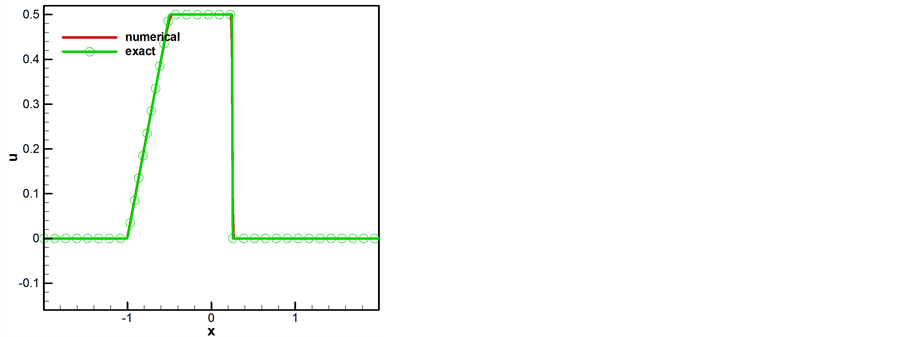
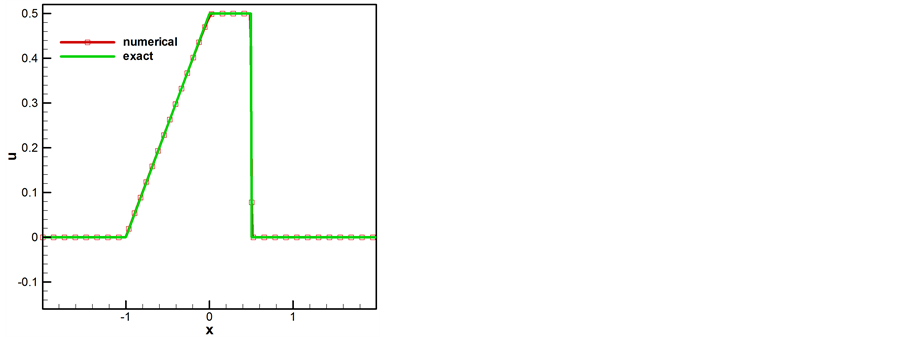
这个例子中要求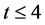 ,在区间
,在区间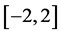 上,选取
上,选取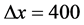 ,t选取1.0和2.0,数值结果在图7中给出。图7表明,该问题的数值解能够很好的近似精确解,mCUI格式能够很好的处理这一类问题。
,t选取1.0和2.0,数值结果在图7中给出。图7表明,该问题的数值解能够很好的近似精确解,mCUI格式能够很好的处理这一类问题。
3.3. 二维线性对流方程
本节我们利用mCUI格式对二维对流方程进行求解,选取Doswell [15] 模型,
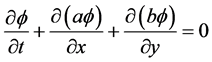
此数学模型在速度场中有稳定的切向速度
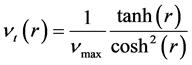
在计算的过程中,我们令 ,并在该场中有
,并在该场中有
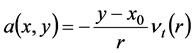 ,
,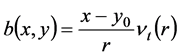
其中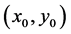 为旋转中心,
为旋转中心,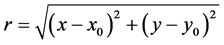 表示区域内任意一点到中心的距离,角速度定义为
表示区域内任意一点到中心的距离,角速度定义为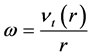 。选取计算区域为
。选取计算区域为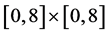 ,等距剖分为
,等距剖分为 的网格,且此模型的精确解为
的网格,且此模型的精确解为
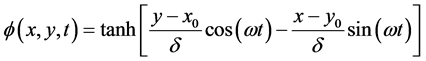
参数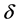 表示的是锋面的梯度,取
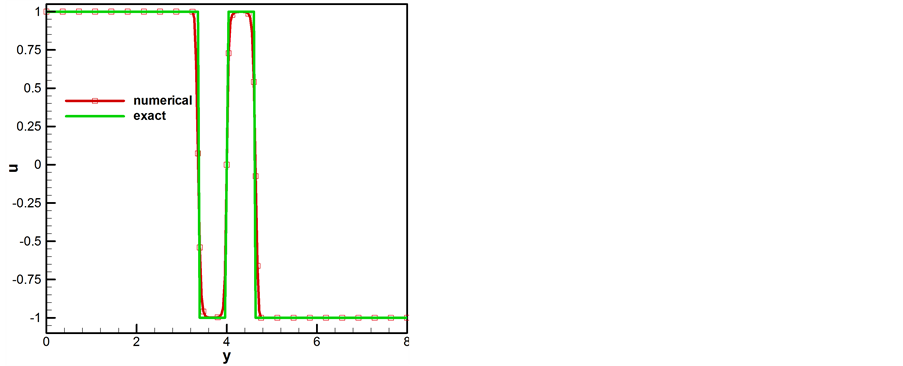
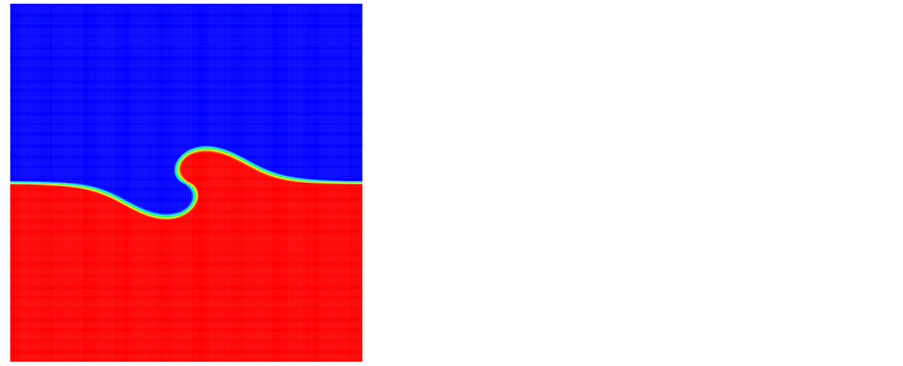
表示的是锋面的梯度,取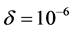 ,得到的数值结果如图8。(a) 是数值解关于在竖直中心线的函数图像,图像表明mCUI格式能够很好的逼近精确解。(b) 显示了数值解的2D图,反应了锋面生成的漩涡形状,(c) 显示了数值解的3D图像。
,得到的数值结果如图8。(a) 是数值解关于在竖直中心线的函数图像,图像表明mCUI格式能够很好的逼近精确解。(b) 显示了数值解的2D图,反应了锋面生成的漩涡形状,(c) 显示了数值解的3D图像。
图6. Burgers方程在不同的扩散系数下的六个不同时间的数值结果,(a) ,(b)
,(b)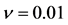 ,(c)
,(c)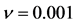 ,(d)
,(d) 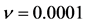
(a)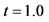 (b)
(b)
Figure 7. Comparison between the exact and numerical solutions for the inviscid Burgers equation at selected time instants, (a) t = 1.0, (b) t = 2.0
图7. Burgers方程数值解与精确解的对比,选取时间为(a) t = 1.0, (b) t = 2.0
 (a) (b)
(a) (b)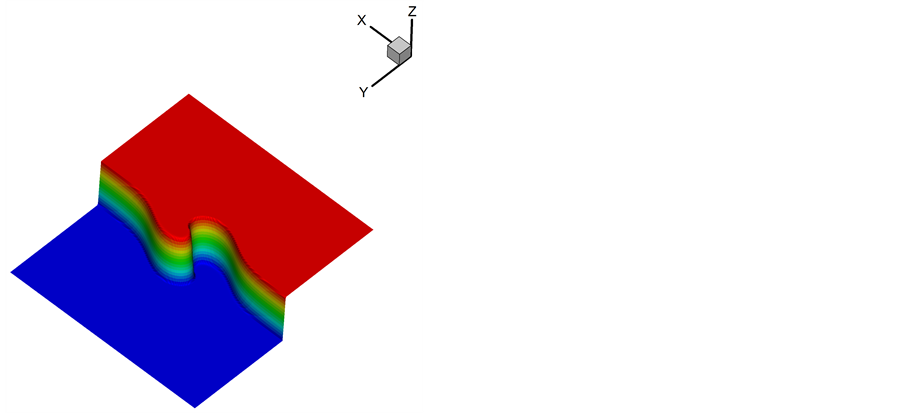 (c)
(c)
Figure 8. Exact and numerical solutions of Doswell and 2D, 3D image
图8. Doswell的数值解和精确解及2D、3D图像
3.4. 二维无粘性Burgers方程
mCUI格式可以解决二维无粘性的Burgers方程
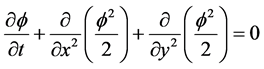
初始条件为
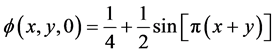
选取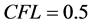 ,
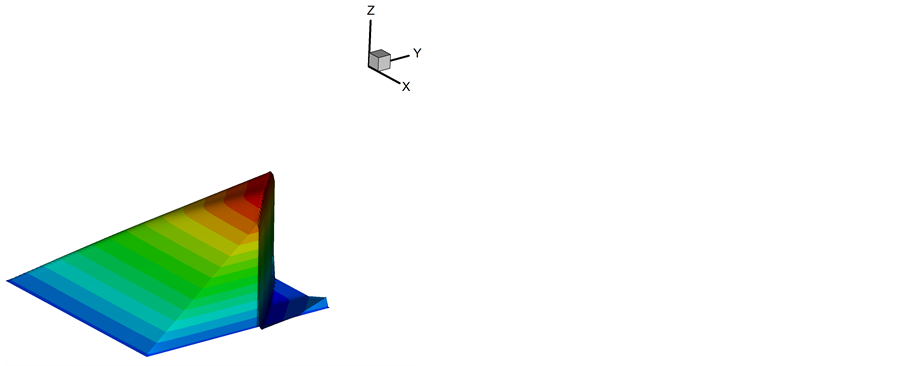
,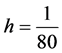 ,图9给出了在时间t = 0.1和t = 0.6时刻下的数值解。图表显示,在t = 0.1
,图9给出了在时间t = 0.1和t = 0.6时刻下的数值解。图表显示,在t = 0.1
时结果依然是光滑的,在t = 0.6时出现了间断,此时在间断附近使用mCUI格式仍然可以得到很好的逼近效果。

 (a) (b)
(a) (b)
Figure 9. The two-dimensional inviscid Burgers equation; computed solutions at two selected time instants. (a) t = 0.1 and (b) t = 0.6
图9. 二维Burgers方程在不同的时刻下的数值解,(a) t = 0.1,(b) t = 0.6
4. 结论
本文基于BAIR准则和TVD准则,结合Hermite插值,构造出高分辨率格式mCUI格式。此格式简单方便,易于计算机实现。经典算例表明,此格式可保证对流稳定性和计算精度。
致谢
作者感谢审稿专家给予本文宝贵的修改意见和建议以及期刊编辑对本文的付出。
基金项目
本文由内蒙古自治区人才开发基金项目(12000-1300020240)和内蒙古自然科学基金项目(2015MS0101)支持。