1. 造斜率影响因素
1.1. 工具结构及其造斜原理的影响
研究发现,导向工具结构是影响造斜率的主要因素,针对不同工具的结构特点和造斜原理,学者们提出的造斜率预测方法常常具有差异性。因此,对工具结构及其造斜原理的深入研究是提出科学的造斜率预测方法的重要前提。
自1962年诞生世界上第一个具有实用性的导向钻具——弯接头加螺杆钻具组合以来 [1] ,定向钻井技术及其导向工具的发展经历了3个里程碑:利用斜向器定向钻井、利用泥浆动力马达定向钻井和利用旋转导向工具定向钻井。
1.1.1. 斜向器
斜向器又称槽式变向器,最早被应用于1895年,是最先出现的导向工具 [2] 。它的造斜原理简单,即是将一个楔形面置于井下,一旦定好方向,便可使钻头继续沿着楔形面旋转钻进,从而可逐步钻离初始方向并侧钻至预设方向,如图1所示。根据钻井需要,上述钻进过程可以不断重复,是一种旋转钻进式、断续式的定向钻井技术。可见,楔形面的倾角(即导斜角)和导斜行程是影响斜向器造斜率的主要结构因素。

Figure 1. Schematic diagram of directional well control with whipstock
图1. 斜向器定向钻井简图
1.1.2. 泥浆动力马达
由泥浆马达提供动力的导向工具是继斜向器后出现的另一突破性定向钻井技术,最早出现于20世纪30年代,是基于螺杆泵理念发展起来的滑动式钻井技术。这种泥浆马达是一种利用钻井液的流动促使钻头旋转的容积式泵,且钻头旋转与钻柱旋转相互独立,后来便发展成当前熟知的螺杆钻具(positive displacement motor, PDM)。钻井工作者发现,配置弯壳体或弯接头可以使导向更高效,所以相继出现了弯接头螺杆钻具和弯壳体螺杆钻具,如图2所示。
对于弯接头螺杆钻具,由于弯接头井下动力钻具的弯曲点到钻头的距离较长(约10 m长),所以当用它进行造斜时,由于受井眼约束的作用,在弯壳体及附近的区域将产生长力臂和比较大的力矩,弯接头以上钻具将会出现弹性变形;从而在钻头处产生侧向力,对井壁进行侧向切削达到造斜的目的。所以许多学者常用力学分析方法对弯接头螺杆钻具进行造斜率分析和预测。其弯接头刚度、弯曲角的大小、与钻头的间距是影响造斜率的主要结构因素。
而弯壳体导向钻具进行造斜时,因弯曲点到钻头的距离较短、刚度相对较大,所以国内外不少学者根据其几何结构和几何关系,运用几何分析法来预测弯壳体螺杆钻具的造斜率;弯壳体的结构弯角、刚度和长度等是其造斜率的主要影响因素。
在以上两种滑动导向钻井中,为提高钻井速度和钻进效率,钻井工作者常常配合转盘钻单–多稳定器钻具组合,如图3所示,以复合钻进的方式进行造斜率的控制。转盘钻单–多稳定器钻具组合是旋转钻进,其机械钻速比螺杆钻具的钻速高,所以在定向钻井时,常在使用螺杆钻具进行造斜后,换用转盘钻稳定器钻具组合继续增斜、稳斜或降斜,两者交替进行直至达到目的层。因稳定器的位置、数量、外径及形状等复杂结构因素的影响,转盘钻单–多稳定器钻具组合造斜率的预测也较复杂,国内外学者常用力学分析法或几何预测法进行其造斜率的预测。
1.1.3. 旋转导向工具
旋转导向工具(rotary steerable systems, RSS),从20世纪90年代末期诞生开始就与MWD和高效能钻头相结合,代表着当前最先进的定向钻井技术。根据工具结构和造斜原理的不同,分为推靠式和指向式两类。推靠式旋转导向工具是基于推靠钻头的偏置原理来导向的,其可变径稳定器的导向块装在不旋

 (a) 弯接头螺杆钻具 (b) 弯壳体螺杆钻具
(a) 弯接头螺杆钻具 (b) 弯壳体螺杆钻具
Figure 2. Directional drilling of screw drill
图2. 螺杆钻具定向钻井简图

Figure 3. Schematic diagram of typical rotary drilling single-multi-stabilizer BHA
图3. 典型转盘钻单-多稳定器钻具组合简图
转套筒上,其典型结构由不旋转外套和旋转驱动轴2大部分构成,不旋转外套上设置有井下CPU、测量控制部分、液压系统和偏置执行机构,通过上、下轴承对旋转驱动轴提供旋转支撑,旋转驱动轴上接钻柱,下接钻头,起传递钻压、扭矩和输送钻井液的作用,如图4(a)所示。指向式旋转导向工具典型结构如图4(b)所示,也是一种不旋转外筒式导向工具,不同之处在于它不是靠偏置钻头进行导向,而是靠不旋转外筒与旋转心轴之间的一套偏置机构使旋转心轴偏置,从而为钻头提供一个与井眼轴线不一致的倾角,产生导向作用。其偏置机构是一套由几个可控制的偏心圆环组合形成的偏心机构,当井下自动控制完成组合之后,该机构将相对于不旋转外套固定,从而始终将旋转心轴向固定方向偏置,为钻头提供一个方向固定的倾角。可见两者结构都很复杂,其造斜率预测更加复杂,国内外有学者运用几何分析法或力学分析法对旋转导向工具进行造斜率预测。
1.2. 其他影响因素
除此以外,造斜率影响因素还包括以下几个方面 [3] [4] :① 钻井操作参数的影响,主要包括钻压、钻头扭矩、钻井液浮力及机械转速等因素;② 井眼几何参数的影响,主要包括井眼视半径、井眼曲率、井斜角、方位角及井径变化等因素;③ 地层因素的影响,主要包括地层可钻性(包括横观和法向2个方向)、地层的几何产状(包括地层的倾角和倾向方位角)、地层的软硬交错(综合可钻系数)、地层方位漂移系

 (a) 推靠式旋转导向工具 (b) 指向式旋转导向工具
(a) 推靠式旋转导向工具 (b) 指向式旋转导向工具
Figure 4. Schematic diagram of directional drilling with rotational steerable tool
图4. 旋转导向工具定向钻井简图
数及地层中裂缝、孔洞的存在等因素;④ 钻头因素的影响,主要包括钻头各向异性指数(涉及结构形式、类型及尺寸等因素)、钻头侧向切削能力、钻头偏转角及钻头方位漂移特性等因素。
在上述造斜率影响因素中,导向工具的类型与结构和钻头因素是可控因素;井眼几何参数和地层因素是随机的、不可控因素;而钻井操作参数虽然可以控制,但仍具有波动性,加之这些因素的耦合影响直接导致了造斜率预测的难度和复杂性。基于此,国内外钻井界的学者们提出了不同的造斜率预测方法,有的主要考虑工具的结构,有的主要考虑工具的受力,有的以数理统计为基础、根据钻井经验和实际钻井数据建立造斜率预测模型;可以归纳为几何预测法、力学预测法、回归分析预测法3大类。
2. 现有造斜率预测方法与分析
2.1. 几何预测法
几何预测法是根据导向工具的结构与井壁的几何关系推出,不考虑工具的受力与变形、地层和钻头的各向异性、工具外径、井径扩大率及钻井工艺参数等影响因素,计算简便,但误差较大。最典型的是“三点定圆法”,其后又发展了“双半径法”和“修正的三点定圆法”。1985年,Karisson等人 [5] [6] 率先针对井底钻具组合提出了“三点定圆法”来预测造斜率。1990年,Hassen等人 [7] 提出了“双半径法”来预测中长半径水平井的造斜率。随后,王宝新等人 [8] 拓展了“双半径法”的应用范围,帅健等人 [9] 应用三点定圆的数学方程给出了几何造斜率的预测方法,苏义脑等人 [10] 对双弯和三弯钻具与单弯钻具的等效关系问题进行了深入研究。唐雪平等人 [11] 提出了“修正的三点定圆法”,考虑了钻头、稳定器尺寸和井眼扩径对弯壳体螺杆钻具造斜率的影响,分析了其对造斜率影响的敏感程度,比较全面地反映了实际情况。刘修善 [12] [13] 在上述研究成果的基础上,考虑了弯角位置和稳定器与井壁间隙对导向钻具造斜率的影响,补充和完善了“修正的三点定圆法”。Sugiura [14] 基于简单几何原理给出了推靠式和指向式两类旋转导向工具的造斜率公式,原理推导类似于弯壳体马达的“三点定圆”造斜率公式,由于忽略旋转导向工具结构和钻井工艺等参数对造斜率的影响,加之完全刚性的假设,导致计算误差较大。闫铁等人 [15] 采用“修正的三点定圆法”,针对不同类型弯壳体导向钻具组合进行了造斜能力预测,并绘制出了造斜能力随影响因素变化的影响曲线图。近两年,李兴伟、张胜杰等人 [16] [17] 将“修正的三点定圆法”应用于弯壳体螺杆钻具造斜率的预测和现场技术服务中。
2.2. 力学预测法
力学预测法是建立在对导向工具受力变形分析基础上,进行造斜率的预测和分析。根据计算原理的不同,代表方法有平衡曲率法、极限曲率法、钻头与地层相互作用预测理论。
2.2.1. 平衡曲率法
平衡曲率法最早由Birades等人 [18] [19] 于1988年提出,认为下部钻具组合总是沿着使自身消耗能量最小的方向钻进,即随着机械进尺的增加,钻头侧向力将逐步减小,当趋于零时:钻具达到保持恒定曲率的稳定状态,此井眼曲率即为平衡曲率。该方法根据建立在不同坐标系下的钻速方程表达式和井斜角、方位角表达式及曲率增量表达式对实钻井眼进行模拟和预测。于永南等人 [20] 运用平衡曲率法进行了短半径水平井中双弯井底马达造斜率的计算和预测,提出了提高双弯井底马达造斜率的方法。孙健等人 [21] 采用平衡曲率法,对大角度单弯螺杆造斜率进行了计算,确定了螺杆钻具组合极限应力与造斜率的关系。
2.2.2. 极限曲率法
极限曲率法是指底部钻具组合的钻头侧向力为零时所对应的井眼曲率。Murphey和Cheatham [22] 最早用钻头侧向力为零时的井眼曲率来预测实际的钻进曲率。苏义脑 [23] 发展和完善了这种理论,推导了“极限曲率法”的预测模式,即首先通过导向工具受力变形分析,求得钻头处侧向力为零时的井眼曲率值,该曲率值为极限曲率,然后根据钻井实践引入两个系数,分别求得导向工具的造斜率和造斜性能。2000年,唐雪平等人 [11] 综合运用极限曲率法和修正的三点定圆法来预测中短半径水平井弯壳螺杆钻具的造斜率,选择了4种典型的双弯螺杆钻具组合的结构参数和工艺参数对造斜率进行了预测和敏感性分析,用现场数据验证得到了较好的预测结果。2008年,于宗仁等人 [24] 对煤田地质勘探钻孔中孔底动力螺杆钻具组合进行了力学实验研究,用极限曲率法进行了造斜率预测,并结合现场定向施工资料对研究的结果进行了验证,预测值与实际值基本相符。2011年,唐雪平等人运用变刚度梁柱理论,建立了中短半径水平井造斜螺杆钻具组合的力学模型,得到了钻头侧向力的计算模型,然后运用极限曲率法对钻具组合进行了造斜率的预测和工程实践验证。
2.2.3. 钻头与地层相互作用预测理论
钻头与地层相互作用综合考虑钻头与地层的性能,是一种通过钻井实践和室内实验不断发展起来的预测理论,主要有各向异性地层理论、地层造斜力理论、三维钻速方程、侧向切削模型、横观各向同性地层有限元模式及机械比能理论等。
Ho [25] 和高德利等人 [26] 把地层看作横观各向同性,分别建立了NL模型和矩阵模型对造斜率进行预测。高德利通过分析稳定器的安放位置对钻头力学特性的影响,来分析和预测转盘钻稳定器钻具组合的造斜性能;Pastusek等人 [27] 综合考虑钻头侧向切削响应和BHA力学行为,基于室内试验和有限元分析提出了推靠式旋转导向工具的造斜率预测模型,预测性能较好,但试验工作量大且计算复杂,应用性受限。张建群和阎铁 [28] 在综合考虑钻头各向异性和地层各向异性的基础上建立了三维钻速方程,结合钻柱力学分析即可预测造斜率,刘永辉等人 [29] 则在此基础上对造斜率预测模型做了改进。Noynaert [30] 提出了一种基于机械比能(mechanical specific energy, MSE)理论预测造斜率的方法,研究了MSE对造斜率/狗腿严重度的影响。使用这种方法,在整个钻井过程中,只需要最小的调整就可以根据已钻井眼获得良好的造斜率预测结果;他用实验数据研究了造斜率、机械转速(rate of penetration, ROP)与MSE之间的关系,并用多个地质导向钻进的页岩气钻井数据进行了测试,测试表明这种方法对于预测造斜率是稳健而又精确的。
2.3. 回归分析预测法
回归分析预测法是建立在数理统计基础上,利用已得的实钻数据资料进行统计分析、建立模型进而对造斜率进行预测。
王俊良等人 [31] 以转盘钻稳定器钻具组合的造斜率预测为研究对象,利用一阶线性回归方法统计同一地区已钻过的定向井资料,对地层硬度、井眼尺寸进行分类处理,建立了与5个变量相关的造斜率预测模型。柳贡慧等人 [32] 提出利用二阶正交多项式回归分析法预测钻具造斜率,是在极限曲率法的基础上,考虑钻压、井径、装置角和井斜角4个影响因素的波动范围对造斜率的影响,建立回归模型和求解;该方法涉及二阶项,若增加影响因素分析数量,则需要大大增加钻井数据资料和训练样本。
2.4. 三类方法的分析比较
综上所述,几何预测法是根据导向工具的几何结构推出,忽略力学因素和井下复杂环境的影响,计算成本小,效率高,常用于斜向器和弯壳体螺杆钻具的平均造斜率预测,但工程应用表明预测精度并不高,误差较大。力学预测法能综合考虑多种因素,计算精度较高,但计算成本高,计算效率低;其中,平衡曲率法通常不考虑地层的各向异性,其预测精度取决于BHA的力学分析精度,计算过程复杂,效率往往不高;极限曲率法,预测原理与平衡曲率法基本相同,是通过两个经验系数综合考虑除地层特性参数外的多种影响因素,一定程度上提高了造斜率预测精度,但这两个系数的选取受使用者钻井经验的限制,且预测精度还受力学分析模型和计算方法的影响;钻头与地层相互作用预测理论,从理论上讲都能够较准确地预测造斜率,但这些模型都涉及较多的地层参数和钻头参数,如地层和钻头的各向异性指数、地层方位漂移系数、钻头侧向切削能力等,这些参数又都会因油田、区块、井深的不同而存在较大差异,在实际应用中很难选取,加上计算过程复杂,所需的条件和假设在许多场合无法满足,因此该方法在实际的钻井工程应用中也受到限制。回归分析预测法进行造斜率预测的相关研究较少,目前为止仅见文献 [31] 和 [32] ,都是运用了常见的多元回归分析方法,而且文献 [31] 的一阶线性回归并不能很好地反映造斜率与其影响因素间的复杂关系,文献 [32] 的二阶多项式回归模型虽然拟合效果较好,但对训练样本的数目依赖性较高,随着自变量的增加,需要的训练样本的数量将成倍增长,而且它对训练样本非常敏感,可能会因为训练样本微小的变化而产生很大的、无法预知的波动,造成拟合函数的失真和预测性能的降低。
3. 基于Kriging代理模型的造斜率预测新方法
几何预测法和力学预测法主要是通过几何分析和静力学分析得出的一系列理论公式,常用试验或数值模拟来计算,不仅预测结果不能完全符合钻井实践,而且预测过程常需耗费大量的资源和计算成本,尤其是在复杂地层中。从实际应用效果来看,几何法预测精度不够高,力学法计算繁杂不便于推广应用,科学性与高效性均欠佳。回归分析法是基于已得的实钻数据资料进行统计分析,有较高的科学合理性,且在钻井工程领域一直应用广泛。在回归分析方法中,Kriging代理模型是解决“模糊性、随机性和非线性”问题的有效方法,它能够较好拟合高度非线性过程,可以很好地解决“多输入单输出”问题,具有计算量小、精确插值和预测精度高等优点。Chen等人 [33] 在基于可靠性的设计优化中,使用Kriging模型克服了大量计算成本耗费的问题,提高了计算效率。
Kriging代理模型是一种基于统计理论、充分考虑变量空间相关特征的插值技术 [34] [35] ,能够较好拟合高度非线性过程,解决“多输入单输出”问题,能够精确拟合多个输入与单个输出之间的函数关系,被广泛应用于地质统计学领域,来预测矿藏、油藏等的分布、储量及产量等 [36] [37] ,近几年在目标优化、工程设计优化、可靠性分析、稳健参数设计等领域成为研究的热点 [38] [39] [40] ,研究表明该方法具有计算量小、精确插值和预测精度高等优点。
提出采用Kriging代理模型的方法对造斜率进行预测,能在尽量不消除、不减少不确定因素的情况下,使各种影响因素(非线性的、随机的、模糊的)引起造斜率波动的方差尽可能小,通过小训练样本建立代理模型,拟合多种影响因素这一“多输入”与造斜率这一“单输出”之间的函数关系,然后用测试样本进行预测值估计和预测性能评价,从而可以指导定向井的井眼轨迹控制,提高造斜率预测精度和计算效率,同时达到节省造斜时间和降低钻井成本的目的。
基于Kriging代理模型进行造斜率预测的具体步骤是:
1) 设计试验方案及收集钻井现场数据,选取造斜率主要影响因素作为输入参数。
2) 确定训练样本和测试样本。训练样本主要用于Kriging模型的构建,测试样本主要用于Kriging模型的预测性能评价。
3) 输出超参数。以预测残差平方和为指标,采用交叉验证法,求解出Kriging模型的最佳超参数。
4) 构建Kriging模型。基于步骤3中的最优超参数,构建Kriging模型。
5) 预测测试样本。根据步骤4所构建的模型,在测试样本处估计预测值。
6) 计算预测指标。根据步骤5中测试样本处的预测值,计算均方根误差(root-mean-square error, RMSE)、最大绝对误差(maximum absolute error, MAE)和平均绝对误差(average absolute error, AAE) 3个常见的预测指标 [41] [42] 的数值。RMSE、MAE和AAE这个指标均是用来计算预测值与真实值的差,值越小,表明模型的造斜率预测精度越高,预测性能越好。其中,3个指标的计算公式如下:
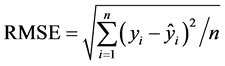 (1)
(1)
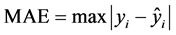 (2)
(2)
 (3)
(3)
式中:n是测试点的个数;yi和 分别为第i个试验点的真实值与预测值。
分别为第i个试验点的真实值与预测值。
7) 评价预测性能。根据3个预测性能指标数值,综合评价Kriging模型的预测性能。
如何根据造斜率影响因素来选择Kriging代理模型的输入参数,以确保造斜率预测的精度,是使用该方法的关键问题。具体的输入参数选取,应在充分分析已钻邻井数据资料的基础上,从所用导向工具的结构因素、钻头因素、地层因素、井眼几何参数和钻井操作参数中选取确定,应是造斜率的显著影响因素;而且,输入参数可以是钻井的实测数据,也可以是根据实测数据通过计算而得出的间接数据,但用间接数据,建议使用相同的计算方法,以减少预测误差。为了预测造斜率,验证Kriging代理模型的拟合效果和预测性能的优越性,可选取其他常用回归分析模型(如多项式模型、RBF模型、神经网络模型等)分别计算RMSE、MAE和AAE这3个造斜率预测性能指标,与Kriging模型的预测指标进行比较,评价Kriging模型的造斜率预测性能。
4. 结论
造斜率预测在定向井尤其是复杂定向井开发中具有举足轻重的作用,精确而又高效的造斜率预测不仅可以提高井眼轨迹控制精度,降低井眼轨迹控制难度,而且可以提高定向井开发效率,降低钻井成本。针对导向工具造斜率预测的困难性与复杂性问题,通过对现有方法的调研与分析,将回归分析方法引入到造斜率预测方法中,提出了基于Kriging代理模型的造斜率预测新方法。
1) 分析了影响导向工具造斜率的主要因素,着重分析了导向工具结构与造斜原理的差异对造斜率的影响,主要包括斜向器、泥浆动力马达和旋转导向工具三类。
2) 调研分析了国内外学者们提出的造斜率预测方法,主要有几何预测法、力学预测法和回归分析预测法,指出几何法预测精度不够高,力学法计算繁杂不便于推广应用,科学性与高效性均欠佳。回归分析法是基于已得的实钻数据资料进行统计分析,有较高的科学合理性,从回归分析法的角度提出计算量小的基于Kriging代理模型的造斜率预测新方法。
3) 结合诸多影响因素与造斜率之间的非线性的、随机的、模糊的复杂关系,提出了基于Kriging代理模型的造斜率预测新方法,阐明了该预测方法的预测机理和预测步骤,并进一步说明了该方法的通用性、实用性、高效性和科学性。
基金项目
石油天然气装备教育部重点实验室(西南石油大学)项目(OGE201403-01);湖北省教育厅科学研究计划中青年人才项目(Q20151301);国家自然科学基金项目(51275057)。