1. 引言
考虑常系数Sobolev方程的定解问题:
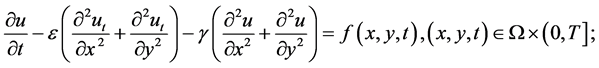 (1)
(1)
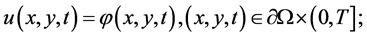 (2)
(2)
 (3)
(3)
其中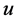 为未知函数,
为未知函数,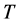 为终结时间,
为终结时间,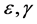 为正常数,
为正常数,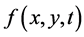 、
、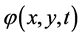 、
、 分别为为源函数、边值与初值,且都是已知函数,
分别为为源函数、边值与初值,且都是已知函数, ,
,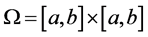 。
。
Sobolev方程是一个重要的数学物理方程,被用来描述流体穿过岩石或土壤及不同介质中的流体运动,土壤中湿气的迁移等 [1] [2] [3] 。由于实际问题中Sobolev方程的源函数、初边值或计算域会很复杂,故有效的求解方法是求其数值解。
关于二维常系数Sobolev方程定解问题(1)~(3)的数值求解,有很多这方面的研究。 [4] - [10] 提出了H1-Galerkin混合有限元方法、最小二乘Galerkin有限元方法、时间间断的Galerkin有限元方法、最低阶的半离散和全离散混合有限元方法以及有限体积元方法等来求解。对于求解Sobolev方程定解问题最有效方法之一的有限差分方法,罗振东等 [11] 提出基于POD (奇异值分解和特征投影分解)降阶外推差分算法。先建立全二阶Crank-Nicolson隐格式,再基于POD方法对C-N格式的降阶外推得到新的差分格式。此格式有效的减少了计算过程中的误差积累,提高了计算效率。但这些处理方法的时间及空间精度均不超过2阶。显然,对问题(1)~(3)研究高精度的数值方法有着重要的实际意义,但就我们的阅读所及,还未见这方面的研究。本文对问题(1)~(3)提出了一个紧致差分格式,证明了该差分格式的解以无穷模范数无条件收敛,且收敛阶是 。数值实验结果表明理论结果是正确的。在数值计算时,系数矩阵为三对角块矩阵,我们采用块三对角追赶法求解以提高计算效率。
。数值实验结果表明理论结果是正确的。在数值计算时,系数矩阵为三对角块矩阵,我们采用块三对角追赶法求解以提高计算效率。
2. 差分格式的建立
2.1. 一些记号
首先对区域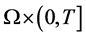 上进行网格剖分。引入
上进行网格剖分。引入
符号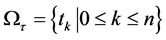
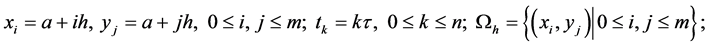 。其中
。其中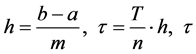 分别表示空间步长与时间步长,
分别表示空间步长与时间步长,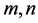 取整数。设指标集
取整数。设指标集
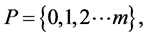 。
。
设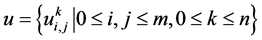 为
为 上的网格函数,记
上的网格函数,记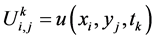 ,类似地定义网格函数
,类似地定义网格函数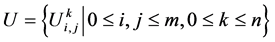 。
。
引入如下记号:
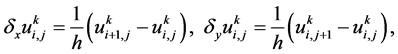
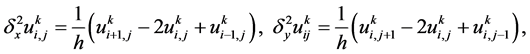
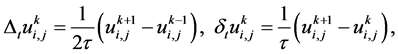


设 为
为 上的网格函数,定义范数:
上的网格函数,定义范数:

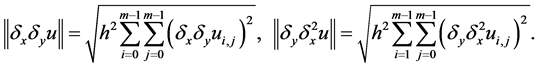
类似的可以定义:
我们还用到:

2.2. 差分格式
在点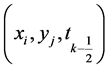 处考虑微分方程(1)
处考虑微分方程(1)
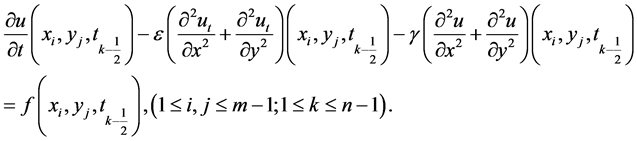 (4)
(4)
由Taylor展开式
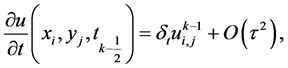 (5)
(5)
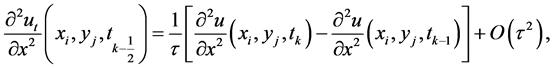 (6)
(6)
 (7)
(7)
 (8)
(8)
 (9)
(9)
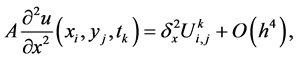 (10)
(10)
 (11)
(11)
将(5)~(9)式代入(4)式得到:
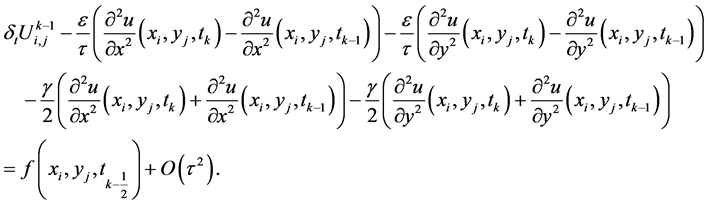 (12)
(12)
对(12)式左乘算子AB,再利用(10)和(11),因算子A、B可交换,故有:
 (13)
(13)
即:
 (14)
(14)
其中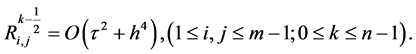
由(2)~(3)初边值条件,我们可以得到:
 (15)
(15)
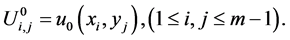 (16)
(16)
略去小量项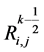 ,将
,将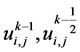 替换
替换 ,得到定解问题(1)~(3)的紧致差分格式:
,得到定解问题(1)~(3)的紧致差分格式:
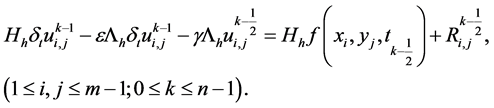 (17)
(17)
 (18)
(18)
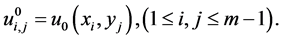 (19)
(19)
3. 数值解的先验估计
引理1:设 为
为 上的网格函数,且
上的网格函数,且 ,
,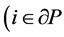 或
或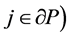 ,则有:
,则有: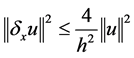 。
。
证: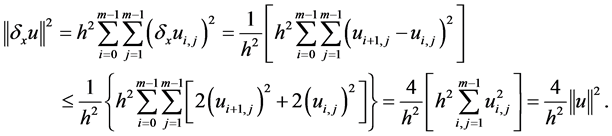
类似的 方向也有相同的结论。
方向也有相同的结论。
引理2 [12] :设 为
为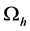 上的网格函数,则
上的网格函数,则 。
。
引理3 [12] :对于时间序列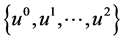 和
和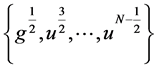 ,任意的
,任意的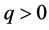 。有:
。有:

引理4 [12] :假设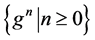 是一个非负序列,
是一个非负序列, ,并且非负序列
,并且非负序列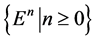 满足
满足
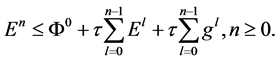
那么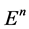 满足
满足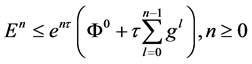 。
。
定理1:设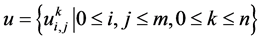 为差分方程
为差分方程
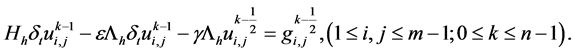

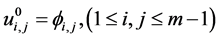
的解,其中 ,那么
,那么
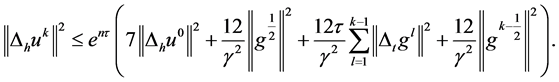 (20)
(20)
证:在差分方程两边分别与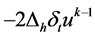 作内积,得:
作内积,得:
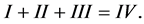 (21)
(21)
其中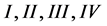 计算分别如下,
计算分别如下,
由引理1,有:
 (22)
(22)
由引理1,有:
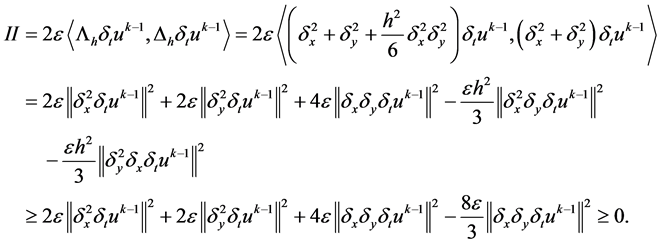 (23)
(23)
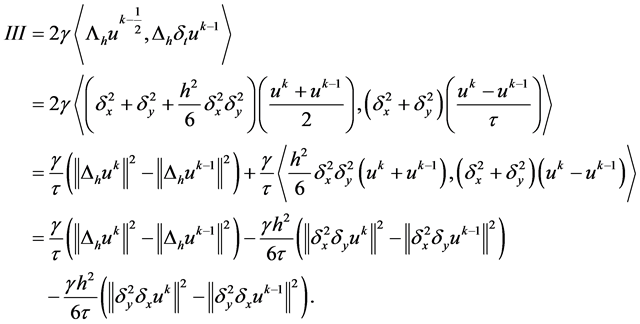 (24)
(24)
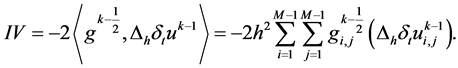 (25)
(25)
将(22)~(25)代入(21),然后不等式两边同乘以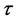 ,得:
,得:
 (26)
(26)
令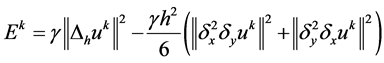 。则(26)式有:
。则(26)式有:
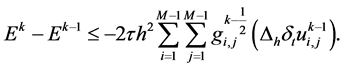
递推之即得:

由引理3,取 ,有:
,有:
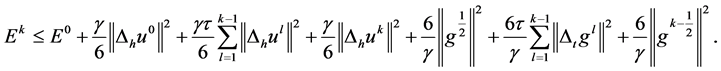 (27)
(27)
又因为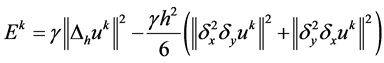 。由引理1
。由引理1
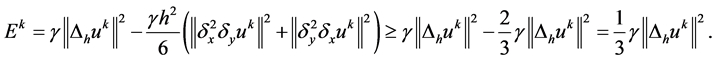
故:
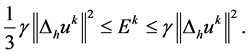
由上式及(27)式,有
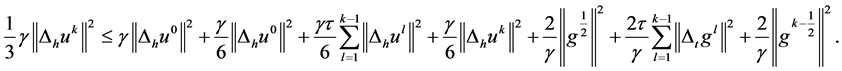
将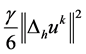 移项,不等式两边再同乘以
移项,不等式两边再同乘以 ,有:
,有:
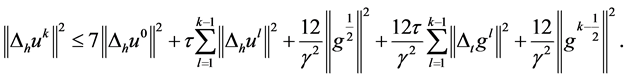
又由引理4,有:

4. 差分格式的收敛性与稳定性
定理2:设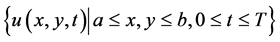 为定解问题(1)~(3)的解,
为定解问题(1)~(3)的解,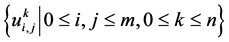 为差分格式(17)~(19)的解,记
为差分格式(17)~(19)的解,记 。
。
那么
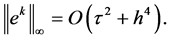
证:式(14)~(16)减去(17)~(19)得到误差方程
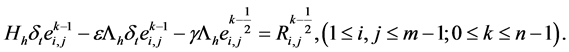 (28)
(28)
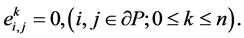 (29)
(29)
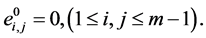 (30)
(30)
由定理1的(20)式和引理2,则存在常数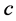 ,有:
,有:
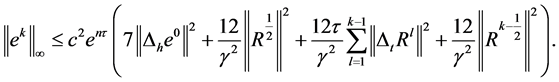
又由 故:
故:

类似地,可以证明数值解的稳定性。
定理3:在定理2的条件下差分格式(17)~(19)的数值解依无穷模范数无条件稳定。
5. 数值算例
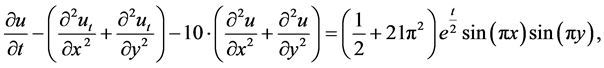

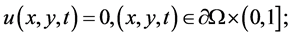
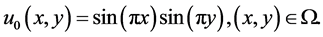
其中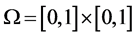 ,定解问题的精确解
,定解问题的精确解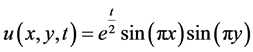 。
。
表1给出了取不同步长时数值解的误差
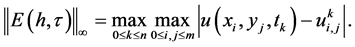
其中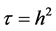 。为了验证此格式收敛阶为
。为了验证此格式收敛阶为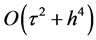 ,利用公式
,利用公式
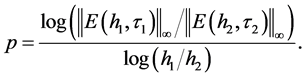

Table 1. Errors of numerical solution and convergence rate of example at different step sizes
表1. 取不同步长时数值解的误差及收敛比率
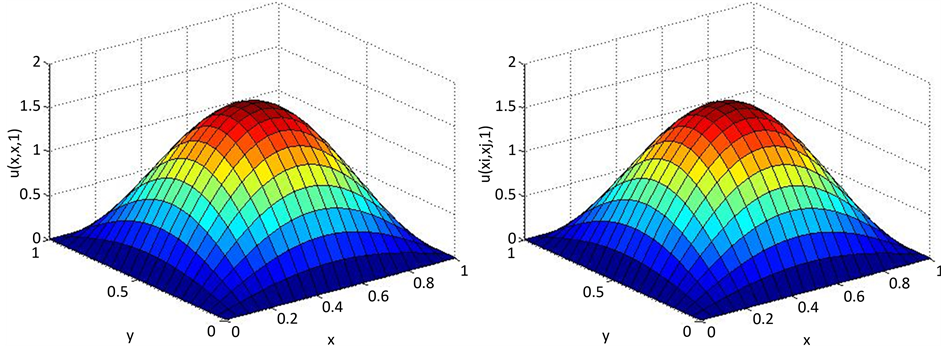
Figure 1. The surface of exact solution and numerical solution when t = 1 (h = 1/20, τ = 1/400)
图1. t = 1时的精确解曲面(h = 1/20, τ = 1/400)与数值解曲面
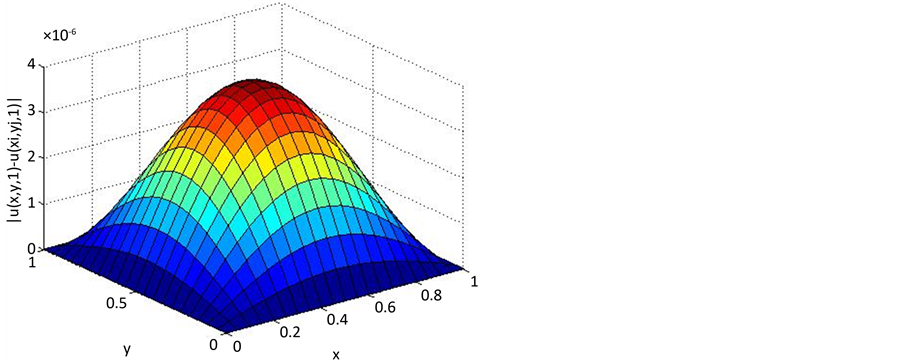
Figure 2. The surface of absolute error when t = 1 (h = 1/20, τ = 1/400)
图2. t = 1时的误差曲面(h = 1/20, τ = 1/400)与数值解曲面
计算出相邻两次取不同空间步长时的比率 。从表1中可以看出比率
。从表1中可以看出比率 接近4,从而验证了此格式的收敛阶为
接近4,从而验证了此格式的收敛阶为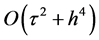 。图1为算例
。图1为算例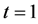 时的精确解曲面与数值解曲面
时的精确解曲面与数值解曲面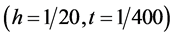 。可以看出此格式的数值解与精确解是吻合的。图2为算例
。可以看出此格式的数值解与精确解是吻合的。图2为算例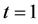 时的误差曲面
时的误差曲面 。进一步说明了此格式求解的准确性。
。进一步说明了此格式求解的准确性。