1. 引言
考虑高阶函数方程
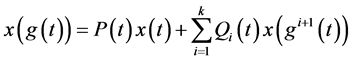 (1.1)
(1.1)
其中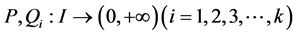 ,
, 是一个给定的函数,
是一个给定的函数,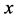 是一个未知函数,
是一个未知函数,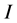 是
是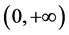 上的无界子集。
上的无界子集。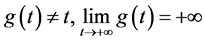 ,
,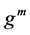 表示函数
表示函数 的
的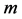 次迭代,即:
次迭代,即:
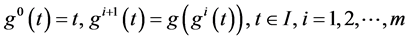
如果函数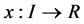 使得
使得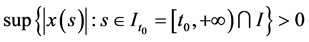 对
对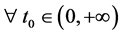 成立,且对
成立,且对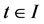 满足(1.1)则称其为方程(1.1)的一个解。这样的解称作是振动的。
满足(1.1)则称其为方程(1.1)的一个解。这样的解称作是振动的。
当 时方程为:
时方程为:
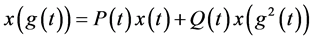 (1.2)
(1.2)
其中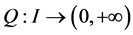 是给定的函数。
是给定的函数。
微分方程和离散变量的差分方程的振动理论在过去几十年中已经得到广泛地发展,最近带有连续变量的差分方程的振动性研究也得到迅速的发展。然而函数方程以离散变量和具连续变量的差分方程作为其特殊情形,且函数方程以及具有连续变量的差分方程解的振动性的研究也越来越受到人们的重视(参见 [1] - [15] )。1994年,Golda和Werbowski [1] 首先对方程(1.2)的解的振动性做了研究,从他们的研究中我们可以知道,如果
 (1.3)
(1.3)
或
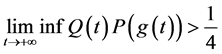 (1.4)
(1.4)
时方程(1.2)所有的解振动。
同时他们也将(1.3)推广到:
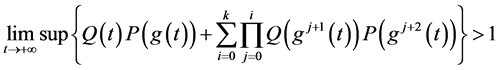 (1.5)
(1.5)
那么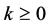 是一个整数。
是一个整数。
1995年,Nowakowska和Werbowsk [2] :将条件(1.4)推广到方程
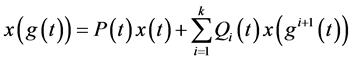
 (1.6)
(1.6)
或
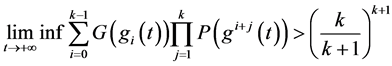 (1.7)
(1.7)
其中
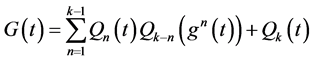 (1.8)
(1.8)
1999年,周勇和俞元洪 [3] 研究方程(1.1)的解的振动性。他们证明了方程(1.1)的所有解振动,如果
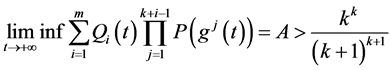 (1.9)
(1.9)
或
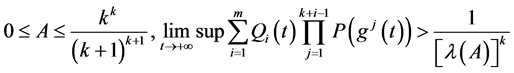 (1.10)
(1.10)
 是方程
是方程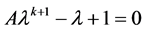 在
在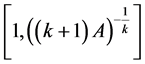 上唯一的实根。
上唯一的实根。
本文我们在文 [4] [5] 的基础上,研究了方程(1.1),得到一切解振动的几个充分条件。
2. 主要定理及相关证明
引理1.1. 假设,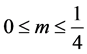 ,
,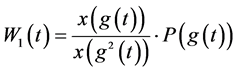 ,
, ,
,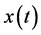 是方程(1.1)的最终正解,那么
是方程(1.1)的最终正解,那么
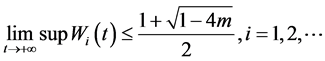 (2.1)
(2.1)
证明:由(1.1)有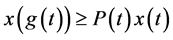
因为当 时,
时, ,有
,有
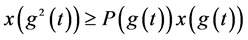 (2.2)
(2.2)
又因为
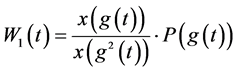
故有
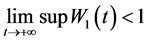
当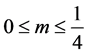 ,对任意
,对任意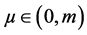 ,有
,有
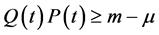 (2.3)
(2.3)
由(2.2)得
令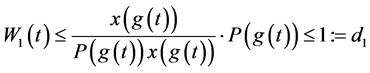 ,即
,即
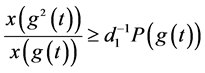 (2.4)
(2.4)
由(1.1)、(2.3)和(2.4)有
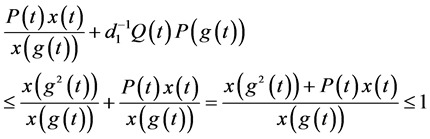 (2.5)
(2.5)
将(2.3)代入(2.5)中,有
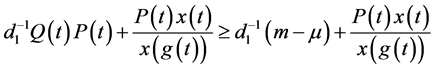
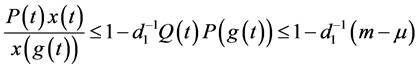
即

于是得到
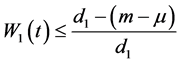
令
同理可得
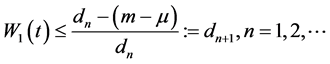
并且由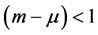 得
得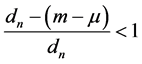 。
。
则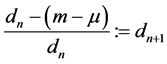 是单调递减,即
是单调递减,即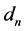 也是单调递减。
也是单调递减。
令 使得
使得 成立。
成立。
所以,由
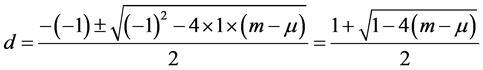
可得
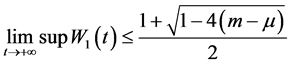
当 ,得到(2.1)即有
,得到(2.1)即有
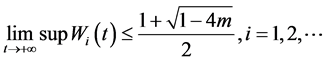
以上是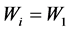 时的证明。
时的证明。
下证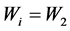
由(1.1)有
 (2.6)
(2.6)
且
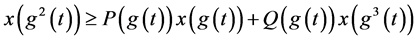 (2.7)
(2.7)
由上述可知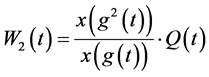 。
。
因为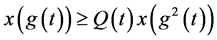 ∴
∴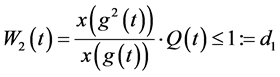 。
。
因此,当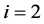 时,假定
时,假定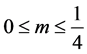 任意
任意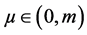 有
有
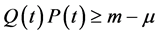 (2.8)
(2.8)
由(2.7)得
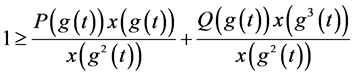
因为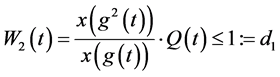 ,
,
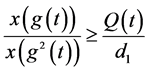 ,
,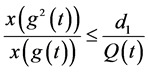
又由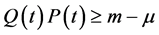
∴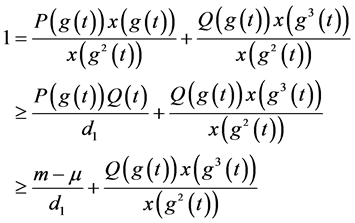
由此可得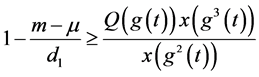 ,
,
所以有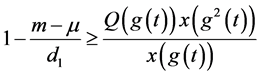 ,
,
即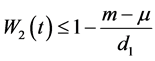 令
令 ,
,
则有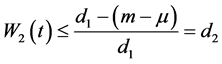 。
。
同理可得,如此巡回的过程得到
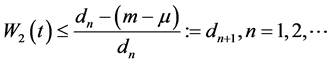
故
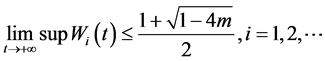
定理1.1. 假设
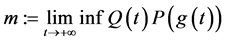 ,
,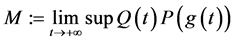 (2.9)
(2.9)
当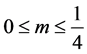 ,
,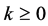 的整数,且
的整数,且
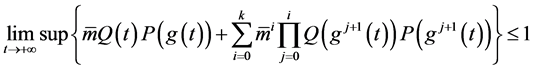 (2.10)
(2.10)
那么方程(1.1)的一切解是振动,这里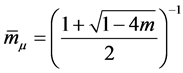 。
。
由(1.1)对于任意足够小 ,
,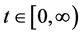 得到不等式
得到不等式
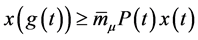 (2.11)
(2.11)
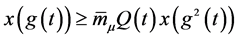 (2.12)
(2.12)
这里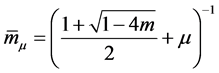 。
。
由(2.11)得到
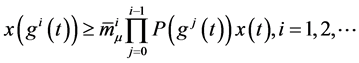 (2.13)
(2.13)
由(2.7)归纳有
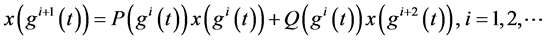 (2.14)
(2.14)
由(2.7)和(2.14)对于 的整数
的整数
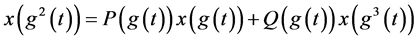
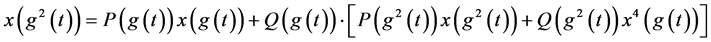
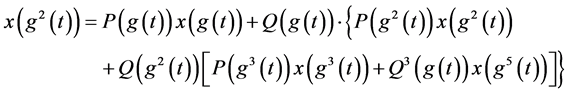
如此重复上述过程可得
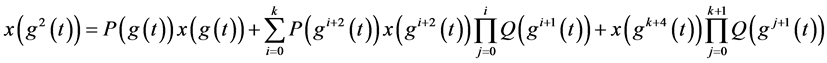
对于(2.12)和(2.13)得到
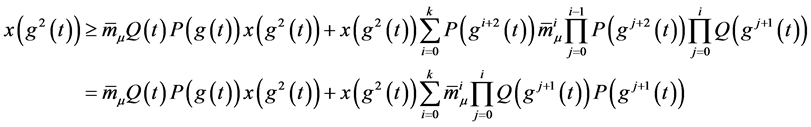
两边除以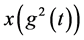 取极限且
取极限且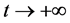 ,得到
,得到

令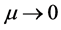 有
有 。证毕
。证毕
定理1.2. 当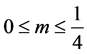 时,而且
时,而且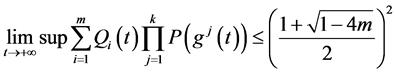 ,
,
那么方程(1.1)的所有解振动。
证明:当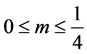 时,对任意
时,对任意 当
当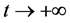 时由(2.3)迭代有
时由(2.3)迭代有
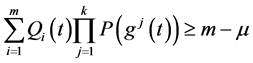
由(2.1)得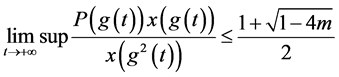 ,且
,且
 (2.15)
(2.15)
将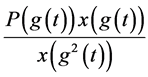 与
与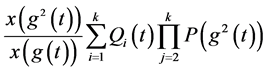 两式相乘必存在
两式相乘必存在
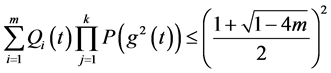
最终得到
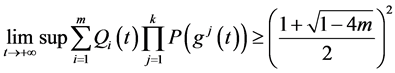
所以,当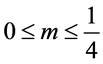 时,满足
时,满足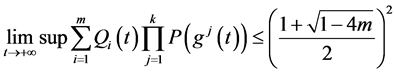 ,那么方程(1.1)的所有解振动。于是定理1.2得以证明。
,那么方程(1.1)的所有解振动。于是定理1.2得以证明。
定理1.3. 当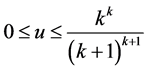 满足
满足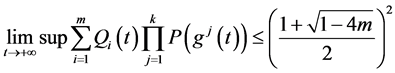
那么方程(1.1)的所有解振动。这里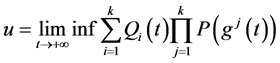
证明:由(2.1)得: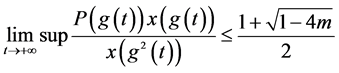
由(2.15)得
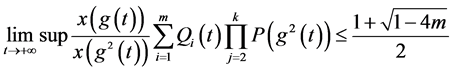
将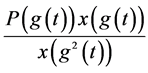 与
与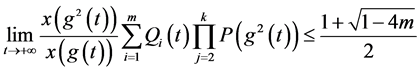
两式相乘必存在
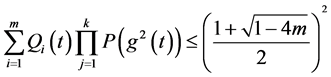
于是得到: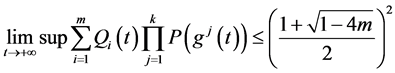 证毕。
证毕。
定理1.4. 当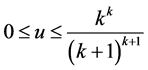 时
时 的整数,并且满足
的整数,并且满足
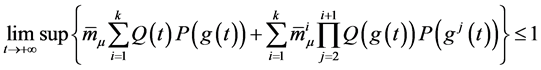
那么方程(1.1)的一切解是振动,这里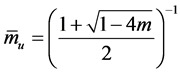
证明:假设(1.1)有解,存在一个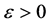 ,且
,且 时
时
 (2.16)
(2.16)
由(2.16)迭代可得
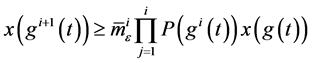
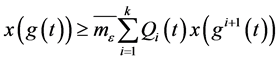
有
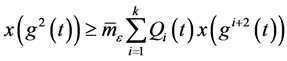
由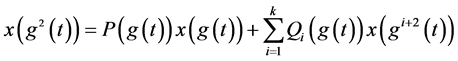
得到: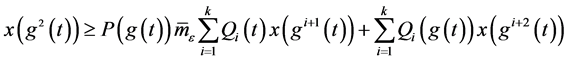

两边同时除以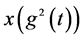 得到
得到
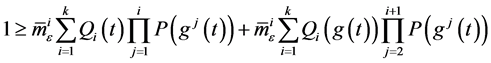
当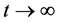 时,得到
时,得到
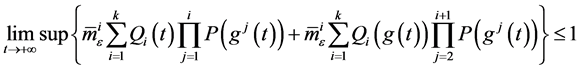
时方程(1.1)有最终正解。引理证毕。
引理1.2. 假设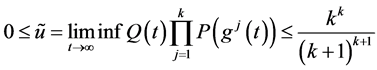 ,
, 是方程
是方程
 ,
, (2.17)
(2.17)
的一个最终正解,那么 。
。
这里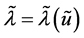 是方程
是方程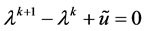 在
在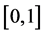 上的最大实根。
上的最大实根。
证明:由方程(1.1)有
 (2.18)
(2.18)
且 通过(2.18)迭代,得
通过(2.18)迭代,得
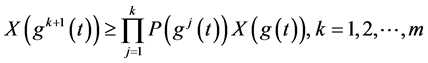 (2.19)
(2.19)
将(2.19)代入(2.17)式得
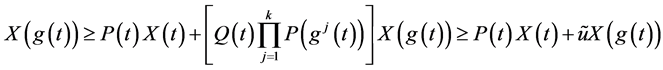
从而有 且
且
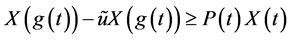
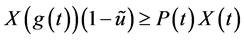

令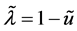
当 时
时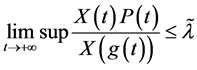
这里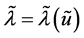 是方程
是方程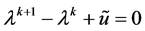 在
在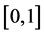 上的最大实根。证毕。
上的最大实根。证毕。
定理1.5. 假设
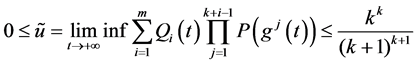
那么方程
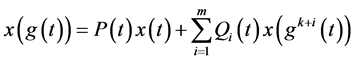 ,
,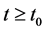 (2.20)
(2.20)
的所有解振动。如果

其中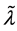 由引理1.2确定。
由引理1.2确定。
证明:由于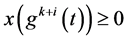 ,通过(2.18)迭代,得
,通过(2.18)迭代,得
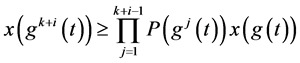 ,
,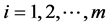 (2.21)
(2.21)
将(2.21)代入(2.20)式,得
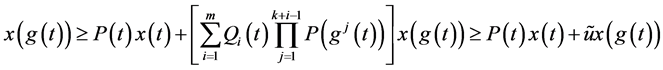 (2.22)
(2.22)
从而有 由引理(1.2)得
由引理(1.2)得 ,即
,即 。
。
由(2.22)得
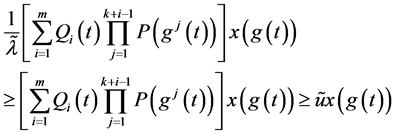
由定理1.2得 且
且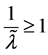 。
。
则
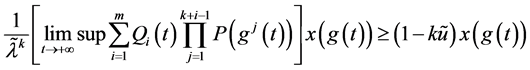
下面证明之
当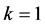 时,
时,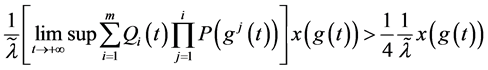
因为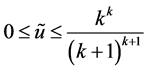 即
即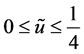
则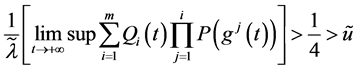
事实上,若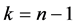 ,则
,则
 (2.23)
(2.23)
成立。
下面证明
当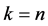 时
时
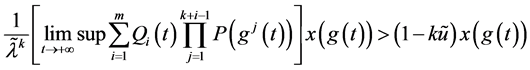 (2.24)
(2.24)
将(2.23)代入(2.20)式,得
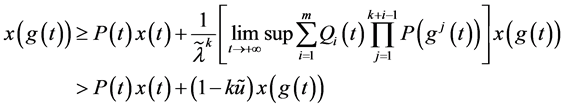
故由归纳法之(2.24)式成立
则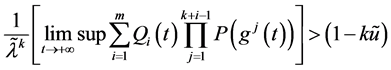
即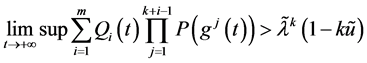
其中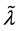 由引理1.2确定。定理证毕。
由引理1.2确定。定理证毕。
基金项目
国家自然科学基金(No:11271380);茂名市科技局软科学项目(No:2014083;2015038)。
NOTES
*通讯作者。