1. 引言
E. N. Lorenz在研究气象模型时,在一类确定性系统中发现了类似于随机的动力学现象,即混沌行为,并于1963年提出了首个混沌数理模型,Lorenz系统 [1] 。由于混沌行为的特殊性,自从Lorenz系统被提出以后,大量来自于不同领域的数学家、物理学家及工程师们便对混沌的起源、混沌系统的特征与分岔行为、通向混沌的路径等各个方面,都展开了深入的研究 [2] [3] [4] 。超混沌,作为另一种复杂动力学行为,它比混沌行为具有更强的复杂性以及更强的应用潜力。由于在自治常微分方程系统中要产生超混沌行为,要求系统维数必须至少为四维,因此,对四维超混沌系统的研究,尤其是对四维Lorenz型超混沌系统的研究,将显得尤为重要。
在对混沌系统的研究中,系统分岔行为的研究是非常重要的一部分。随着系统平衡点稳定性的改变,即发生局部分岔行为,系统的局部动力学行为也会随之改变,甚至会引发系统全局动力学行为的变化。Hopf分岔是系统局部分岔中非常基本而又至关重要的一种, Hopf分岔的发生将伴随着系统极限环的产生或者消失。在三维混沌系统的研究中,文献 [5] 研究了统一Lorenz型系统的Hopf分岔行为,该系统包含了Lorenz, Chen, Lu及Yang等大量的经典三维混沌系统,在此基础上,进一步对退化Hopf分岔进行分析,该文献还发现了一种可通向混沌的路径。在四维超混沌系统的研究中,文献 [6] [7] [8] 分别研究了一类四维超混沌系统的Hopf分岔行为,得到了系统在Hopf分岔点的特性,包括分岔的周期解、周期解的分岔方向及稳定性等。
基于经典的三维Lorenz混沌系统,文献 [9] 通过线性反馈控制方法,得到了如下形式的四维超混沌系统:
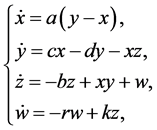 (1)
(1)
其中参数满足 ,
, 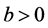 ,
,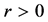 。当系统参数选取
。当系统参数选取 ,
, 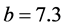 ,
,  ,
,  ,
, 及
及 时,系统(1)具有超混沌吸引子,该吸引子所对应的Lyapunov指数为
时,系统(1)具有超混沌吸引子,该吸引子所对应的Lyapunov指数为

该超混沌吸引子在 空间的投影相图如图1所示,其中红色的点为系统在该参数下的三个平衡点。文献 [9] 证明了该超混沌系统在一定参数条件下存在着属于原点平衡点的一对对称的同宿轨。
空间的投影相图如图1所示,其中红色的点为系统在该参数下的三个平衡点。文献 [9] 证明了该超混沌系统在一定参数条件下存在着属于原点平衡点的一对对称的同宿轨。
当系统参数满足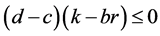 时,系统(1)只具有唯一平衡点
时,系统(1)只具有唯一平衡点 。而当
。而当 时,系统(1)除了具有原点平衡点
时,系统(1)除了具有原点平衡点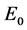 之外,还将具有另外两个关于
之外,还将具有另外两个关于 轴对称的非原点平衡点。
轴对称的非原点平衡点。

其中, 。
。
针对四维Lorenz型超混沌系统(1),本文将研究该系统原点平衡点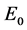 处发生的Hopf分岔行为。
处发生的Hopf分岔行为。
2. Hopf分岔分析
针对一般的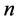 维自治常微分方程系统
维自治常微分方程系统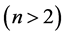 ,下面首先介绍一下第一Lyapunov系数
,下面首先介绍一下第一Lyapunov系数 的计算方法。
的计算方法。
考虑如下的微分方程系统
 (2)
(2)
其中 为
为 中的
中的 类函数。假设系统(2)在参数条件
类函数。假设系统(2)在参数条件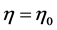 之下具有平衡点
之下具有平衡点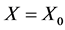 ,并且总是将变量
,并且总是将变量 记为
记为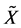 。进一步地,在参数条件
。进一步地,在参数条件 之下,系统(2)可以被重写为
之下,系统(2)可以被重写为
 (3)
(3)
其中
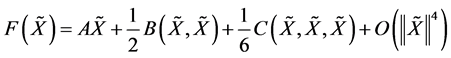
以及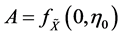 ,并且对任意的
,并且对任意的 ,都有如下展开式成立
,都有如下展开式成立
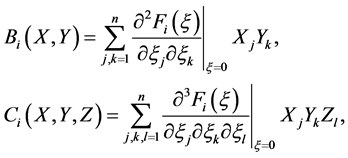 (4)
(4)
其中的记号 以及
以及 分别是向量函数
分别是向量函数 以及
以及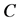 的第
的第 个分量。
个分量。
假设系统(3)在其原点平衡点处的Jacobian矩阵 ,具有一对非零虚部的纯虚特征根
,具有一对非零虚部的纯虚特征根 ,并且Jacobian矩阵
,并且Jacobian矩阵 在该平衡点处的其它特征值都具有非零实部。令
在该平衡点处的其它特征值都具有非零实部。令 为Jacobian矩阵
为Jacobian矩阵 对应于特征值
对应于特征值 的特征向量所张成的广义特征空间。
的特征向量所张成的广义特征空间。
令向量 满足下列条件
满足下列条件
 (5)
(5)
值得注意的是,空间 中的任意向量
中的任意向量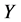 均可以表示成为
均可以表示成为 ,其中
,其中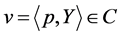 。为了能够通过变量
。为了能够通过变量 以及
以及 来将与特征值
来将与特征值 有关的这个二维中心流形参数化表示,特考虑如下这个形式上的嵌入
有关的这个二维中心流形参数化表示,特考虑如下这个形式上的嵌入
 (6)
(6)
其中系数 ,并且满足
,并且满足 。将表达式(6)代入系统(2)中,可得
。将表达式(6)代入系统(2)中,可得
 (7)
(7)
求解由等式(7)中 项的系数所确定的线性方程组,可得复向量
项的系数所确定的线性方程组,可得复向量 的表达式。因此,在二维中心流形上通过使用复变量
的表达式。因此,在二维中心流形上通过使用复变量 ,系统(7)可以表示成如下形式:
,系统(7)可以表示成如下形式:

其中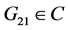 。
。
第一Lyapunov系数 被定义为
被定义为
 (8)
(8)
其中
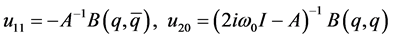 (9)
(9)
在如下的定理中,对系统(1)在平衡点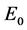 处所发生的Hopf分岔进行了研究。
处所发生的Hopf分岔进行了研究。
定理1. 令 ,以及
,以及
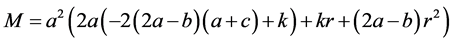 (10)
(10)
 (11)
(11)
并且假设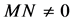 成立,则当参数
成立,则当参数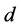 穿过临界值
穿过临界值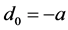 时,系统(1)在平衡点
时,系统(1)在平衡点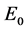 处发生Hopf分岔。在临界参数值附近,系统还有如下的动力学性质:
处发生Hopf分岔。在临界参数值附近,系统还有如下的动力学性质:
1) 如果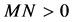 ,则当
,则当 时,相空间中存在由Hopf分岔所产生的不稳定周期轨;
时,相空间中存在由Hopf分岔所产生的不稳定周期轨;
2) 如果 ,则当
,则当 时,相空间中存在由Hopf分岔所产生的稳定周期轨。
时,相空间中存在由Hopf分岔所产生的稳定周期轨。
证明:令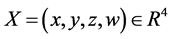 ,
, 以及
以及

则系统(1)可被改写成系统(2)。
系统(1)在平衡点 处的特征方程为
处的特征方程为
 (12)
(12)
当系统参数满足 时,方程(12)具有一对纯虚特征根
时,方程(12)具有一对纯虚特征根 ,其中
,其中

在参数条件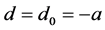 之下,系统(1)在平衡点
之下,系统(1)在平衡点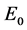 处的Jacobian矩阵为
处的Jacobian矩阵为
 (13)
(13)
其所对应的特征值为
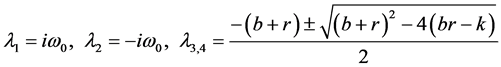
经过繁琐地计算过程,可得如下的两个特征向量:
 (14)
(14)
向量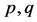 满足条件(5),即
满足条件(5),即
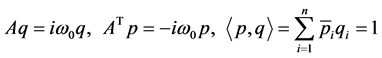
由计算公式(4),可得
 (15)
(15)
基于公式(13), (14)及(15),通过直接而繁琐地计算,可得
 ,
, 
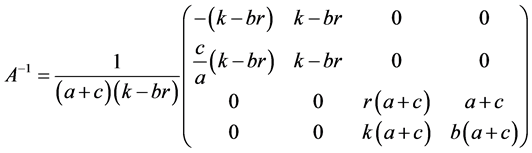
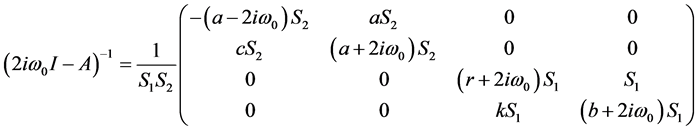
其中
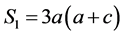 ,
, 
因此,可以得到
 (16)
(16)
再次使用公式(14), (15)以及(16),可计算得

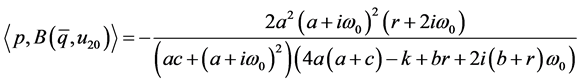

将上述三个等式代入(8)式中,可计算得第一Lyapunov系数为
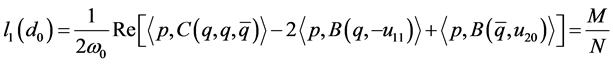
其中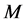 和
和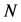 如(10)及(11)所示。因此,如果
如(10)及(11)所示。因此,如果 ,在平衡点
,在平衡点 处所发生的Hopf分岔将产生出不稳定周期轨。否则,如果
处所发生的Hopf分岔将产生出不稳定周期轨。否则,如果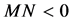 ,在平衡点
,在平衡点 处所发生的Hopf分岔将产生稳定周期轨。
处所发生的Hopf分岔将产生稳定周期轨。
当 时,有
时,有 ,从而有平衡点
,从而有平衡点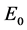 处Hopf分岔的非退化条件成立。进一步,将验证平衡点
处Hopf分岔的非退化条件成立。进一步,将验证平衡点 处Hopf分岔的横截条件也成立。平衡点
处Hopf分岔的横截条件也成立。平衡点 处的特征方程如(12)所示,即
处的特征方程如(12)所示,即

其中
 ,
, 
当参数 在临界值
在临界值 附近时,假设特征方程(12)具有特征值
附近时,假设特征方程(12)具有特征值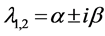 及
及 ,其中
,其中
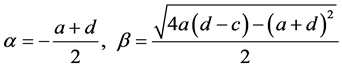
为系统参数的实函数。由于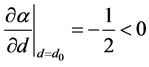 , Hopf分岔的横截性条件成立,并且在由复共轭特征值
, Hopf分岔的横截性条件成立,并且在由复共轭特征值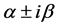 对应的特征向量所张成的特征空间中,分别当
对应的特征向量所张成的特征空间中,分别当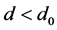 及
及 时,平衡点
时,平衡点 为不稳定及稳定的。
为不稳定及稳定的。
综上所述,系统(1)限制在由平衡点 的复共轭特征值
的复共轭特征值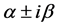 对应的特征向量所张成的特征空间中时,具有如下的动力学行为:
对应的特征向量所张成的特征空间中时,具有如下的动力学行为:
1) 如果 ,则当
,则当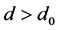 时,相空间中存在由Hopf分岔所产生的不稳定周期轨;
时,相空间中存在由Hopf分岔所产生的不稳定周期轨;
2) 如果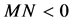 ,则当
,则当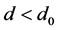 时,相空间中存在由Hopf分岔所产生的稳定周期轨。
时,相空间中存在由Hopf分岔所产生的稳定周期轨。
3. 数值模拟
为了验证定理1中关于系统(1)平衡点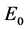 处Hopf分岔理论结果的正确性,特给出了如下基于四阶Runge-Kutta方法的数值仿真结果。选择参数
处Hopf分岔理论结果的正确性,特给出了如下基于四阶Runge-Kutta方法的数值仿真结果。选择参数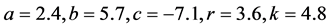 ,根据定理1,可得
,根据定理1,可得 ,
, 及
及 ,这意味着系统(1)在平衡点
,这意味着系统(1)在平衡点 处的Hopf分岔能够产生出稳定的周期轨。当
处的Hopf分岔能够产生出稳定的周期轨。当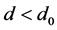 时,Hopf分岔产生稳定周期解,如图2(a)所示;而当
时,Hopf分岔产生稳定周期解,如图2(a)所示;而当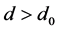 时,平衡点
时,平衡点 为稳定焦点,如图2(b)所示。
为稳定焦点,如图2(b)所示。
基金项目
国家自然科学基金(11626068),广东省自然科学基金(2015A030310424),广东省普通高校特色创新项目(2016KTSCX076)。