1. 研究背景及目的
40多年来,随着近海石油勘探开发和海上运输业的发展,单点系泊技术的发展十分迅速。目前,这种技术已作为一种成熟的海上中转、仓储、过驳技术被世界各国竞相采用。首先,单点作为海上中转终端,通过这种“浮动的码头”,就可以供大型船舶系泊和装卸原油或矿砂,充分发挥了大型船舶运输的优越性。其次,单点作为海上油田采油终端,起到了“浮动油库”的作用,是深海、遥远油田上经济而且先进的储输手段。可以这样说,单点系泊技术为海洋石油开采和海上运输中转的历史翻开了崭新的一页,极大地推动了海洋石油开采业和石油化工业的发展。
单点系泊技术的兴起、发展和应用,对海洋石油开发和提高海上运输效率起到了重要的作用。单点系泊作为一种技术革命,其优势如何?实践证明:首先,单点系泊的最大优势是将码头由岸边移至海上,解决了世界上绝大部分港口航道较窄、较浅、规模较小,不能与大型油轮和超大型油轮发展相匹配的矛盾。
单点系泊源于英文“Single Point Mooring”,简言之,与固定码头相比,它的最大特点即系泊方式是“点”,也就是大型油轮或超大型油轮可以系泊于近海海面上的一个深水“点”,然后进行装卸货操作。
单点系泊码头通常由一个能够漂浮在海面上的浮筒和铺设在海底与陆地贮藏系统连接的管道组成。浮筒漂浮在海面上,油轮上的原油通过漂浮软管进入浮筒后,从水下软管进入海底管线,输到岸上的原油储罐。为防止浮筒随海浪远距离漂移,用数根巨大的锚链将其与海床相连,这样浮筒既可在一定范围内随风浪流漂浮移动,增加缓冲作用,减少与巨轮间发生碰撞的危险,又不至于被海浪漂走。1958年世界第一套单点系泊系统在瑞典作为“海上加油站”成功投产,揭开了单点系泊技术在海洋石油开采和海上原油中转等领域上的应用的序幕。
本文数据建立于2016年全国大学生数学建模,通过建立数学模型讨论下列问题:
1) 建立微分方程组模型,用数值计算的方法分析不同风速下,钢桶和各节钢管的倾斜角度,锚链形状,浮标的吃水深度和游动区域,
2) 第二问在问题一的假设下,调节重物球的质量,使得钢桶的倾斜角不超过5度,锚链与海床的夹角不超过16度。
3)增加了海水的速度,考虑风力、水速和水深等因素的影响并且分析在不同的风速下钢桶,钢管的倾斜角度,锚链形状,浮标的吃水深度和游动区域。
2. 模型的假设
1) 假设本问题所使用的数据真实有效,具有统计分析价值。
2) 前期不考虑海啸、台风等特殊天气对于系泊系统的影响。
3) 假设系泊系统中所有部件都处于理想的平衡状态。
4) 假设系泊系统中各部件连接处光滑。
5) 假定浅海底为水平面,且锚链不发生弹性形变;
6) 假设系泊系统中每个部件所有点的运动情况都相同,大小和形状对研究问题的影响很小,可视为质点。
3. 符号说明
4. 模型的建立及求解
4.1. 问题一
如图1。
4.1.1. 受力分析 [1]
对于问题一,我们首先进行受力分析。
对于浮标(图2)。
对于钢管(图3)。
对于钢桶及设备(图4)。
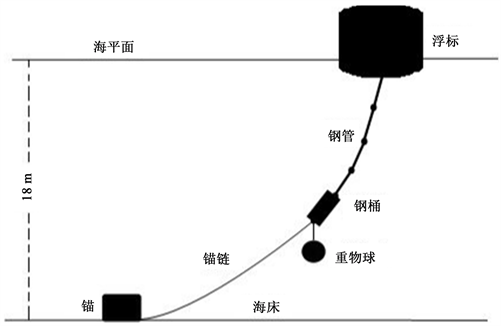
Figure 1. Schematic diagram of mooring system transmission node
图1. 系泊系统传输节点示意图
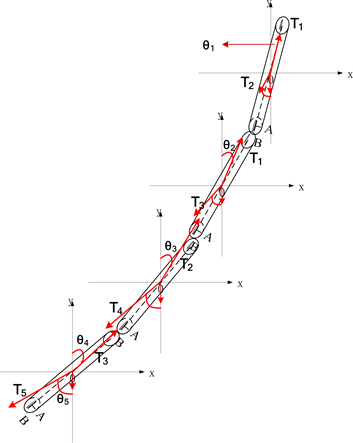
Figure 3. Four sections of steel pipe analysis
图3. 四节钢管受力分析图

Figure 4. Steel drum and equipment force analysis diagram
图4. 钢桶及设备受力分析图
4.1.2. 模型建立:静力学模型的建立 [2]
我们首先选取浮标为研究对象,题中假设海水是静止的,有风时,浮标会产生小的颠簸,在匀速风的作用下浮标将会漂移,但是因为系泊系统将会约束浮标的运动,使得整个系统稳定在一个某个状态下,所以由物理知识我们知道,最终浮标将会处于一个相对平衡的状态,也就是说浮标可以视为处于平衡态。同时整系泊系统可以视为处于平衡状态。
4.1.3. 求解模型
表示浮标的吃水深度,h表示浮标总高度,Fx表示风给浮标的水平力,则有:
(1-1)
由阿基米德原理我们得知浮标所受的浮力
为
(1-2)
由于浮标处于平衡态,可以得到:
(1-3)
其中
表示浮标所受重力,
,
表示浮标的质量,已知浮标质量为1000 kg。钢管共四节,
表示最上面的钢管对浮标的拉力。
表示第一节钢管与垂直方向的倾斜角度为
。
把钢管抽象为一个质点,对连接浮标的第一节钢管进行受力分析,有:
(1-4)
其中
表示钢管的重力,
,
表示钢管的质量,已知钢管的质量为10 kg。
表示第一根钢管与第二根钢管之间的相互作用力,
表示第二根钢管与垂直方向的夹角。
对第二根钢管进行受力分析,有:
(1-5)
其中,
表示钢管的重力,
。
对第三根钢管进行受力分析,有:
(1-6)
其中,
表示钢管的重力,
。
表示第三根钢管与第二根钢管之间的相互作用力,
表示第三根钢管与垂直方向的夹角。
表示第四根钢管与第三根钢管之间的相互作用力,
表示第四根钢管与垂直方向的夹角。
对第四根钢管进行受力分析,有:
(1-7)
其中,
表示钢管的重力,
。
表示钢筒与第四根钢管之间的相互作用力,
表示第四根钢管与垂直方向的夹角。对钢桶受力分析,有
(1-8)
表示锚链与钢筒之间的相互作用力,
表示钢桶与垂直方向的夹角。GT为钢筒自重,Gq为重物球重力。
经过分析,得知各个角度和海水的深度18 m之间存在如下关系:
(1-9)
对上述方程进行求解时,先变形为方程(1-10),再进行求解。
(1-10)
利用MATLAB作图,观察W等于0是否成立,做出的曲线与横轴的交点的横坐标即表示浮标吃水深度
的值。当海面风速为12 m/s,用MATLAB作图得到图5曲线:图中横坐标为
,纵坐标为W,曲线中W = 0的点可以得到浮标此时的吃水深度
。
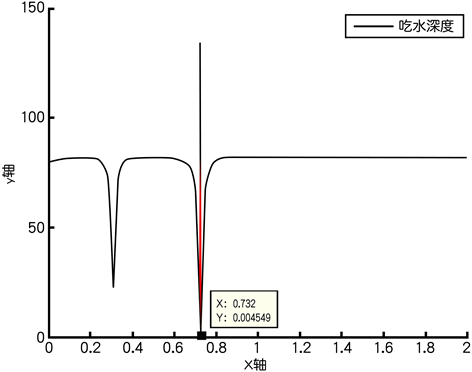
Figure 5. The depth of the draft at 12 m/s (the static water)
图5. 风速12 m/s时吃水深度(水静止)
当海面风速为24 m/s用MATLAB得到图6曲线:
图中横坐标为
,纵坐标为W,曲线中W = 0的点可以得到浮标此时的吃水深度
。
当海面风速为36 m/s我们用MATLAB作图得到图7曲线:
从图像中我们可以看到当风速为36 m/s时,浮标的吃水深度是
。
对于锚链 [3] 我们分析得出:
(1-11)
其中
,
,
(1-12)
由锚链总长22.05 m得
(1-13)
(1-14)
4.1.4. 系泊系统的锚链的非线性有限元计算 [4]
为了改进当前锚链计算方法的不足,我们使用非线性有限元法来计算本系泊系统的响应方式。因为锚链的形状时不确定的,所以在采用索单元模拟系泊系统中的锚链时,用迭代的方式,写出MATLAB代码求出最终平衡状态下的各种参数。通我们对锚链参数进行数值计算,计算出的结果表明用有限元法计算系泊系统是有效的和可行的。
系泊系统的锚链的数学模型

Figure 6. The depth of the draft at 24 m/s (the static water)
图6. 风速24 m/s时吃水深度(水静止)
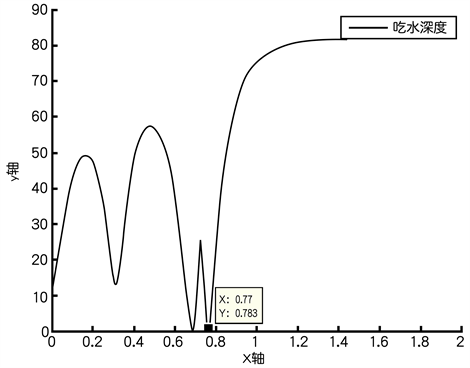
Figure 7. The depth of the draft at 36 m/s (the static water)
图7. 风速36 m/s时吃水深度(水静止)
为了方便推导锚链的数学模型,先建立相应的坐标系。在锚链的时候,建立了两种坐标系:分为两部分,
为总体,
为局部。如图8所示:
(1-15)
(1-16)
(1-17)
上面的方程中:
时锚链的局部曲率半径。进而得到如下关系:
;
;
(1-18)
;
; (1-19)
(1-19)
上式可化为以下矩阵方程:
(1-20)
对矩阵做逆变换得到:
(1-21)
任意变量,在总体
可以表示为:
(1-22)
能这么表示:
(1-23)
可以得到:
(1-24)
设
,其有如下性质:
,
(1-25)
表示单位矩阵。
要想得出系泊系统的锚链的微分方程,只需要截取锚链的某些部分进行受力分析,如图9所示。
(1-26)
(1-27)
锚链在水中的运动,大部分受到法向流体阻力
、切向流体阻
、浮力B,重力W,锚链张力T和惯性力I。设水的速度和系泊锚链的速度的矢量分别时
和
;相对速度矢量和相对加速度矢量分别为
和
,即
(1-28)
(1-29)
设
为
,锚链的两个顶端分别产生的拉力时
,即:
(1-30)
则
(1-31)

Figure 9. Anchor chain stress analysis chart
图9. 锚链受力分析图
(1-32)
法向流体阻力:
(1-33)
切向流体阻力:
(1-34)
净重力:
(1-35)
惯性力:
(1-36)
上述程序中,
分别为水的密度和锚链的密度;
分别为法向阻力系数和切向阻力系数;
为锚链横剖面面积;
为锚链微段;
为系泊系统附加质量系数。
(1-37)
(1-38)
(1-39)
所以可以得到,当锚链处于静止平衡状态时,惯性力
,锚链加速度矢量
,由上述所有方程可以综合得到系泊系统锚链的微分方程
(1-40)
(1-41)
(1-42)
(1-43)
假定锚链净重力(
)远远大于锚链所受到的流体作用力
和
,
(1-44)
(1-45)
为锚链微段与
轴间的夹角,积分上下限分别为
和
,可得
为锚链张力
的水平分力,即
,其中
为锚链张力
的垂向分力;
为锚链初始张力;可以得到
(1-46)
式中
为锚链长度;
为锚链横剖面面积。
因而可以得到锚链张力
,即?
(1-47)
对于锚链上的任意一点
,有
(1-48)
(1-49)
因而
(1-50)
(1-51)
目前,在系泊系统的实际应用中有一种新型锚一沉箱锚被广泛采用。与传统锚相比,
沉箱锚并无抬升角的限制,而传统锚要求抬升角不大于。对于这种沉箱锚,锚链
的下端条件为:
静力问题:
(1-52)
动力问题:
(1-53)
系泊系统锚链的上端条件为:
静力问题:
(1-54)
动力问题:
(1-55)
其中:l为系泊系统锚链总长度,s为Lagrangian坐标,
和
分别为上端点己知位置和速度,
和
分别为下端点已知位置和速度。
本文对系泊系统的锚链通过静力计算和动力估算,作为系统设计依据,并结合有限元分析对锚链的部分进行了强度和张力计算,得到了沿不同深度的最大张力值,为确定各组成部件的强度和安全系数提供了依据,确定了疲劳估算和分析的基础,为锚系受力分析提供了数值依据。
4.2. 问题二
4.2.1. 计算重物球质量范围
根据问题一的模型,建立带约束非线性规划,以求得满足题意的重物球质量的取值范围,根据约束条件
求出目标函数
的最小值和最大值,即为重物球的最小质量和最大质量,用MATLAB软件计算出结果。
目标函数:
(2-1)
约束条件:
(2-2)
计算得出重物球最小质量
,最大质量为
。也就是说重物球取值范围是[1565, 4000] (单位:kg)。重物球质量在这个区间内是有意义且满足题目条件的。
4.2.2. 结果分析
通过MATLAB软件,我们计算出了风速在12 m/s, 24 m/s, 36 m/s下的浮标吃水深度(表2)与钢管的倾斜角度及锚链两端切线与竖直方向夹角(表3)。
由表格对照可以得到以下规律:在海水静止、海床近似水平、风速均匀的前提下,风从各个方向吹来的概率是均等的,因此浮标的游动区域可近似视为一个圆面,圆心落在过锚且垂直于海底的杆上。随着海面风速的提高,系泊系统浮标的吃水深度逐渐加深,浮标的游动区域半径逐渐增大,四节钢管的倾斜程度也逐渐增大。

Table 2. Draft depth and moving area of buoys at different wind speeds (the static water)
表2. 不同风速下浮标吃水深度及游动区域(水静止)

Table 3. The angle of inclination of the steel pipe and the angle between the tangent line and the vertical direction at the ends of the cable at different wind speeds (the static water)
表3. 不同风速下钢管的倾斜角度及锚链两端切线与竖直方向夹角(水静止)
4.3. 问题三
4.3.1. 风力与水流力同向
对于第三问,我们考虑两种特殊的情况:一种是水速与风速同向,另一种是水速与风速反向,其他情况介于这两种的特殊情况之中。
在水速VS = 1.5 m/s的情况下,浮标所受的近海水流力为:
(3-1)
其中,S1表示浮标在水中垂直水速的投影面积,其中
。
第一种情况:基于模型一,只需将模型一中的公式(1-1)中浮标的受到的力Fx1变成
(3-2)
其中,Fx1表示浮标所受的风力和水流力的合力。
当海面风速为12 m/s,用MATLAB软件作图得到图10曲线。
下图可以得到浮标此时的吃水深度
。
当海面风速为24 m/s,用MATLAB作图得到图11曲线。
下图可以得到浮标此时的吃水深度
。
当海面风速为36 m/s,用MATLAB作图得到图12曲线。
下图可以得到浮标此时的吃水深度
。
4.3.2. 风力与水流力反向
对于第二种特殊情况,只需将(1-1)浮标的水平力
变成下式,其余量保持不变。
(3-3)
当海面风速为12 m/s,用MATLAB作图得到图13曲线。
下图可以得到浮标此时的吃水深度
。
当海面风速为20 m/s,用MATLAB作图得到图14曲线。
下图可以得到浮标此时的吃水深度
。
当海面风速为36 m/s,用MATLAB作图得到图15曲线。
下图可以得到浮标此时的吃水深度
。
4.3.3. 结果对比
水速与风速同向时,得到不同风速下浮标吃水深度及游动区域(表4),钢管的倾斜角度及锚链两端切线与竖直方向夹角(表5)。
水速与风向相反时,得到不同风速浮标吃水深度及游动区域(表6)钢管的倾斜角度及锚链两端切线与竖直方向夹角(表7)。

Figure 10. The depth of the draft at 12 m/s (water velocity of 1.5 m/s in the same direction as the wind)
图10. 风速12 m/s时吃水深度(与风同向的水流速1.5 m/s)
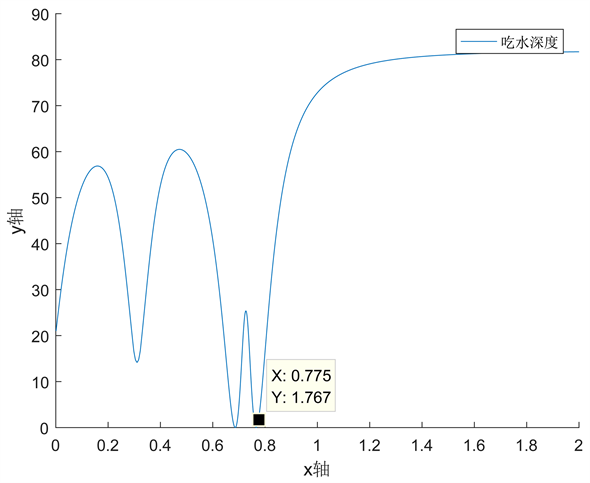
Figure 11. The depth of the draft at 24 m/s (water velocity of 1.5 m/s in the same direction as the wind)
图11. 风速24 m/s时吃水深度(与风同向的水流速1.5 m/s)

Figure 12. The depth of the draft at 36 m/s (water velocity of 1.5 m/s in the same direction as the wind)
图12. 风速36 m/s时吃水深度(与风同向的水流速1.5 m/s)

Figure 13. The depth of the draft at 12 m/s (water velocity of 1.5 m/s in the different direction as the wind)
图13. 风速12 m/s时吃水深度(与风反向的水流速1.5 m/s)
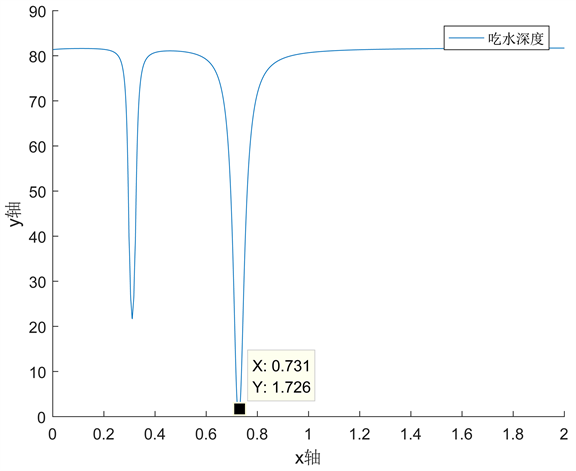
Figure 14. The depth of the draft at 20 m/s (water velocity of 1.5 m/s in the different direction as the wind)
图14. 风速20 m/s时吃水深度(与风反向的水流速1.5 m/s)
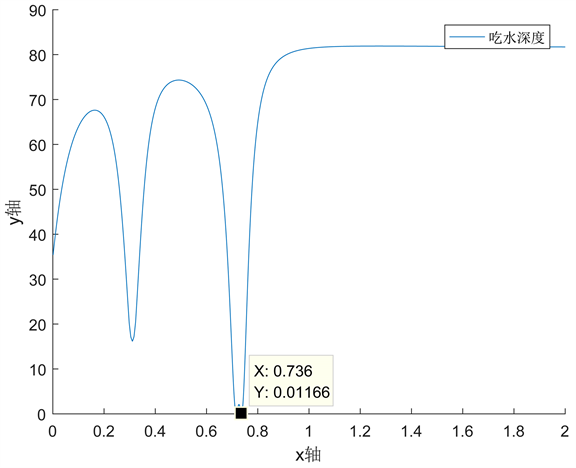
Figure 15. The depth of the draft at 36 m/s (water velocity of 1.5 m/s in the different direction as the wind)
图15. 风速36 m/s时吃水深度(与风反向的水流速1.5 m/s)

Table 4. Draft depth and moving area of buoys at different wind speeds (water velocity of 1.5 m/s in the same direction as the wind)
表4. 不同风速下浮标吃水深度及游动区域(与风同向的水流速1.5 m/s)

Table 5. The angle of inclination of the steel pipe and the angle between the tangent line and the vertical direction at the ends of the cable at different wind speeds (water velocity of 1.5 m/s in the same direction as the wind)
表5. 不同风速下钢管的倾斜角度及锚链两端切线与竖直方向夹角(与风同向的水流速1.5 m/s)

Table 6. Draft depth and moving area of buoys at different wind speeds (water velocity of 1.5 m/s in the different direction as the wind)
表6. 不同风速下浮标吃水深度及游动区域(与风反向的水流速1.5 m/s)

Table 7. The angle of inclination of the steel pipe and the angle between the tangent line and the vertical direction at the ends of the cable at different wind speeds (water velocity of 1.5 m/s in the different direction as the wind)
表7. 不同风速下钢管的倾斜角度及锚链两端切线与竖直方向夹角(与风反向的水流速1.5 m/s)
5. 模型的评价 [5]
5.1. 模型的进步性
静力系统分析是假设在系泊力的作用下处于静止状态,由于系泊系统的各部分都受到平衡力,由此可以计算系泊系统的有关参数。静力学系统的原理分析简单,方法简单实用,大多数情况下可以满足工程应用的精度要求。它的缺点是没有考虑系统中部件的弹性与张力的动力特性。
5.2. 模型的局限性
非线性有限元法可以计算较轻锚链(如尼龙缆或复合缆等)的非线性动力特性而悬链线法无法计算。
在采用非线性有限元法计算锚链在特定激振力作用下的强迫振动响应时,因强非线性几何非线性或材料非线性的存在,导致极值点附近存在较大的计算误差。
在较少的单元数的情况下,高阶单元可以比线性单元更快地收敛到精确解。
在有限元法中,需要将作用于系泊缆索上的流体作用力分别等效在单元的节点上。这个会产生误差。
基金项目
本文得到内蒙古大学自治区级大学生创新创业训练项目支持,项目编号(201610126059)。
[1] 罗晓健, 张爱霞, 李绂. 单点系泊系统设计思路及原则[J]. 中国海洋平台, 2013, 28(2): 19-23.
[2] 王亚洲. 深海单点系泊海洋浮标锚泊系统研究[D]: [硕士学位论文]. 青岛: 中国海洋大学, 2013.
[3] 杨长义, 陈玺文. 浅析系船浮筒锚链的静力计算问题[J]. 港工技术, 2012, 49(2): 18-20.
[4] 肖越. 系泊系统时域非线性计算分析[D]: [博士学位论文]. 大连: 大连理工大学, 2006.
[5] 夏运强, 王绿卿. 浮筒式防风单点系泊系统系泊线特性分析[A]. 全国结构工程学术会议, 2012.