1. 引言
机器人动态规划 [1] 是指在某一个给定的运行空间中,移动机器人通过路径的动态规划来获得一条从初始位置到目标位置的最优路径。环境未知的情况下的机器人路径规划是该领域的研究难点。解决路径规划的主要研究方法包含全局规划法 [2] [3] [4] 和局部规划方法 [5] [6] ,全局规划方法主要包括:神经网络和人工势场的方法、遗传算法和粒子群算法等。而局部规划算法主要包括含滚动路径规划和在线视点寻求方法等。全局规划方法主要解决环境已知的问题,在获取了先验知识后才进行规划,其优点是易于收敛;而局部规划法可以用于解决环境未知或部分可观察的问题,但是其难以收敛,且易于陷入局部最优。
为了更好地利用全局规划方法进行机器人最优规划。文献 [7] 提出了一种多步长的蚁群算法,采用栅格法对机器人的工作环境进行建模,采用启发信息来更新信息素,同时采用最大和最小蚂蚁来限制信息素从而防止算法陷入早熟收敛。文献 [8] 在经典蚁群算法的基础上调整转移概率,设定信息素的上下界,并在规划过程中,根据动态障碍物运行方向来避免碰撞,并对环境突发情况加入Follow_wall行为进行改进。文献 [9] 方法提出了一种改进型目标粒子群算法,实现算法在粒子群之间的信息传递,采用SPEA2的环境选择和配对选择策略来使粒子群收敛到Pareto边界,通过自适应原理来对速度权重进行计算来实现算法的全局和局部搜索能力。文献 [10] 方法设计了一种基于改进混合蛙跳算法实现移动机器人的路径规划,在经典的算法中引入欧氏距离和最优蛙群,通过可调控参数产生新个体来代替随机更新操作,将路径规范问题转换为最小化问题,并根据环境目标和障碍物定义青蛙的适应度,从而实现最优规划。文献 [11] 提出了一种改进的人工势场法求解机器人规划问题,通过对障碍物影响范围进行分层,使得机器人顺利达到目标,并将改进的势场法用于复杂环境的路径规划和路径选择,从而解决由局部极小导致的陷阱问题。
上述工作均研究了机器人的动态规划算法,但仍然存在一些不足,如在面对环境未知情况下容易陷入局部最优,因此,本文提出了一种基于时延Q学习算法的机器人动态规划算法,首先将机器人规划问题建模一个MDP模型,然后定义了基于时延Q学习算法的机器人规划算法,并通过实验证明了文中方法能有效地解决机器人路径规划问题,尤其是在环境未知的情况下,能实现比同类算法更好的性能,具有收敛速度快和求解效率高的优点,适合于环境未知情况下的机器人的最优路径规划。
2. 背景知识
2.1. MDP
机器人与未知环境的交互可以通过一个有限的马尔科夫决策过程(Markov Decision Process, MDP)来进行建模,一个MDP可以建模为一个四元组 ,其中,
,其中, 为所有状态组成的状态空间,任意状态
为所有状态组成的状态空间,任意状态 表示Agent在
表示Agent在 时刻所处的状态;
时刻所处的状态; 是所有动作构成的动作空间,任意动作
是所有动作构成的动作空间,任意动作 表示Agent在
表示Agent在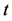 时刻采取的动作;
时刻采取的动作; 是立即奖赏映射函数,
是立即奖赏映射函数, 表示Agent在时刻
表示Agent在时刻 处在状态
处在状态 处,采取动作
处,采取动作 后,迁移到下一个状态
后,迁移到下一个状态 处获得的立即奖赏;
处获得的立即奖赏; 表示状态转移函数,即移动机器人在当前状态
表示状态转移函数,即移动机器人在当前状态 处采取动作
处采取动作 时转移到
时转移到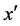 的概率。
的概率。
2.2. Q学习算法
Q学习算法 [12] [13] 是由Watkins等人在1989年首次提出的一种离策略学习算法,属于时间差分(Temporal difference, TD)学习算法的一种,在Q学习算法中,产生样本的行为策略和用于评估的策略不是同一个策略。行为策略往往采用ε-greedy策略,ε-greedy策略即Agent以1-ε的概率选择最优动作,而以ε/|m|的概率选择其他动作,m为动作的个数。评估策略采用的是greedy策略,即贪心策略,在Q学习中,动作值函数的更新可以表示为:
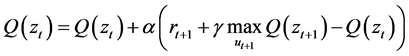 (1)
(1)
3. 基于时延Q学习的机器人动态规划
3.1. 机器人规划的MDP模型
MDP模型需要根据特定的场景进行建模,如对于图1所示机器人规划场景。
为了将图1所示的机器人规划场景进行建模:
状态空间:状态空间需要被离散化,当x轴和y轴都被分为10等份时,Agent可以在这100个位置中的任意一个。因此,状态空间为: ,Agent在任意状态处的位置可以表示为
,Agent在任意状态处的位置可以表示为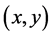 。
。
动作空间:Agent可以采取的动作上下左右四个动作,将动作空间表示为 ,0表示向上的动作,1表示向下的动作,2表示向左的动作,3表示向右的动作。
,0表示向上的动作,1表示向下的动作,2表示向左的动作,3表示向右的动作。

Figure 1. Robot programming experiment scene graph
图1. 机器人规划实验场景图
奖赏函数:Agent每移动一步,将会获得立即奖赏为−1,当agent到达目标时,能获得一个立即奖赏为1,因此,奖赏函数可以被定义为:
 (2)
(2)
迁移函数:Agent每移动一步,当采用向上的动作0时,Agent将会由当前状态 转移到状态
转移到状态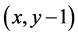 ;当采用向左的动作2时,
;当采用向左的动作2时,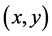 会转移到状态
会转移到状态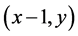 ;当采用向右的动作3时,
;当采用向右的动作3时, 会转移到状态
会转移到状态 ;当采用向下的动作1时,
;当采用向下的动作1时, 会转移到状态
会转移到状态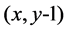 。当遇到障碍物或者墙壁时,agent将会保持在原地不会变化,因此转移函数可以表示为:
。当遇到障碍物或者墙壁时,agent将会保持在原地不会变化,因此转移函数可以表示为:
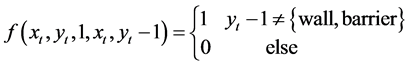
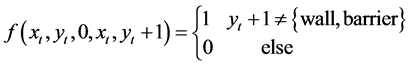
 (3)
(3)
3.2. 机器人规划的目标
强化学习通过最大化长期的累积奖赏来实现状态到动作的最优映射。强化学习算法中通常采用状态值函数或动作值函数来近似表示累积奖赏,动作值函数即Q值函数可以表示为:
 (4)
(4)
最优行为策略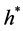 对应的最优Q值函数表示为:
对应的最优Q值函数表示为:
 (5)
(5)
移动机器人规划的目标就是使得式(5)最大化。
3.3. 基于时延Q学习的机器人最优规划算法
经典的Q学习算法仅仅采用ε-greedy贪心策略来实现探索和利用的平衡,通常在算法的运行前期采用比较大的ε值,实现较大的探索,以尽可能学习到较为精确的Q值,而在算法运行的后期,设置比较小的ε值,尽可能地利用已经学习到的策略和Q值。
时延Q学习算法在Q学习算法的基础上主要进行下面两方面的改进:
1) 采用Rmax来对所有状态动作对的Q值设置为 ,使得Agent在初始时刻就开始尽量地探索,因为没有被探索过的状态动作对
,使得Agent在初始时刻就开始尽量地探索,因为没有被探索过的状态动作对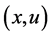 对应的Q值都初始化为最大值,因为会有更高的概率被探索到。
对应的Q值都初始化为最大值,因为会有更高的概率被探索到。
2) 状态动作对 被访问过h次后,才开始更新状态动作对
被访问过h次后,才开始更新状态动作对 的Q值。
的Q值。
基于时间延Q学习的机器人路径规划算法可以描述为:
算法 基于时间延Q学习的移动机器人路径规划算法
初始化:动作总数m,状态动作n,构建机器人路径规划对应的MDP模型,初始化所有状态动作对 的Q值
的Q值 ,折扣因子
,折扣因子 ,资格迹衰减因子
,资格迹衰减因子 ,学习率
,学习率 ;
;
步骤1:状态动作对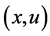 的Q值
的Q值 ,
,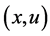 被访问的次数
被访问的次数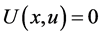 ,
, 为
为 更新的初始时刻,
更新的初始时刻, 为
为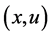 的访问次数,
的访问次数,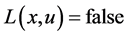 表示是否进行学习,当前时刻
表示是否进行学习,当前时刻 ,误差因子
,误差因子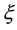 ,计数器阈值
,计数器阈值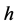 ;
;
步骤2:观察当前的状态 ,然后选择在状态
,然后选择在状态 执行的动作:
执行的动作:
 (6)
(6)
步骤3:执行动作 ,得到下一个状态
,得到下一个状态 ,得到立即奖赏
,得到立即奖赏 :
:
If 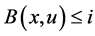 then
then
 ;
;
End If
If  then
then
If  then
then

End If

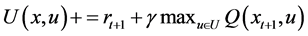
End If
If  then
then

End If
If  then
then

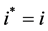
Else if  then
then


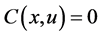
End If
步骤4: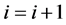 ,
,
If 
转移到步骤2继续执行
Else
转移到步骤5继续执行
End If
步骤5:根据生成的最优状态动作值函数来映射到最优策略:
 (7)
(7)
4. 仿真实验
为了对文中方法进行验证,机器人动态规划系统中机器人的初始状态如图1中的Initial_Position,目标状态为Goal。
算法中参数初始化为:状态动作对 的Q值
的Q值 ,状态动作对
,状态动作对 的访问次数
的访问次数 ,状态动作对
,状态动作对 的最后访问时间
的最后访问时间 ,状态动作对
,状态动作对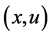 的学习标志
的学习标志 ,迭代次数
,迭代次数 ,误差因子
,误差因子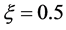 ,计数器阈值
,计数器阈值 。
。
采用文中算法对机器人规划系统进行建模和仿真,最后得到最优策略,根据最优策略获得的任意一条从初始状态Initial_Position到目标状态Goal的路径如图2所示。
为了验证文中算法的优越性,将文中方法与经典的Q-Learning算法以及文献 [11] 中基于蛙跳算法的方法进行比较,得到的三种方法的收敛情况如图3所示。
从图3中可以看出,文中方法不仅具有较快的收敛速度,同时具有最好的收敛解,这表现在文中方法在第50个情节处就开始收敛,收敛的解为13。文献 [11] 所示的蛙跳算法从算法运行开始,收敛速度一直较另外两种方法更慢,在情节数为90时趋于收敛,但收敛的解为局部最优解22步。文献 [11] 采用基于Q学习的方法进行最优策略获取,其算法在运行过程中收敛速度较文中方法更慢,但其在情节为70时收敛,收敛的时间步为23,仍然为局部最优解。显然,文中方法具有最快的收敛速度和最好的收敛解。文中方法没有陷入局部最优解是因为在算法中采用了RMAX方法来增加探索能力,使得初始状态处所有状态动作处都具有较大的Q值,从而使得那些没有访问过的状态动作对能有较大的概率被访问到。文中收敛速度快是因为状态动作对的更新需要根据状态动作对访问的次数来确定,从而使得状态动作更新的效率更高,最终加快了算法的收敛速度。

Figure 2. The robot plans the optimal path
图2. 机器人规划最优路径

Figure 3. Three methods convergent performance comparison
图3. 三种方法收敛性能比较
5. 总结
为了实现对机器人动态规划问题进行求解,设计了一种基于时延Q学习的机器人动态规划方法。首先,介绍了MDP和Q学习的相关背景知识,然后将机器人规划问题规划为MDP模型,并定义了其相关的目标函数。最后,定义了基于时延的Q学习算法来求解机器人行动规划。算法中通过采用Rmax初始化所有状态动作对的Q值来增加探索,同时采用计数器来记录任意状态动作对被访问的次数,从而加快状态动作对的更新。实验结果表明文中方法能有效获取最优路径,且较其它方法具有收敛速度快和收敛效果好的优点,具有很大的优越性。
基金项目
国家自然科学基金项目资助U1433126。