摘要:
若复变函数f(z) 在z0处满足如下极限存在(有限)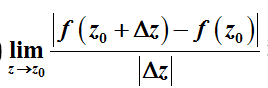 称函数f(z) 于点z0模可导;若f(z) 在z0的某个邻域内的任一点模可导,则称f(z) 在z0模解析。如果函数f(z) 在区域D内任一点模解析,则称(z)为区域D内模解析函数。我们给出了一个复变函数w=f(z)=u(x,y)+iv(x,y) 模解析的如上定义,并导出了模解析函数的必要条件:
称函数f(z) 于点z0模可导;若f(z) 在z0的某个邻域内的任一点模可导,则称f(z) 在z0模解析。如果函数f(z) 在区域D内任一点模解析,则称(z)为区域D内模解析函数。我们给出了一个复变函数w=f(z)=u(x,y)+iv(x,y) 模解析的如上定义,并导出了模解析函数的必要条件: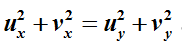 。我们称此为模柯西–黎曼方程(简称模C.-R.方程)。进一步,我们给出了模解析的充分必要条件:(1) u(x,y) ,v(x,y) 在区域D 内满足模C.-R.方程;(2)u(x,y) ,v(x,y) 在区域 D内满足uxuy=-vxvy 。最后,我们讨论了模解析函数与已有的各类复变函数,如解析函数,半解析函数,共轭解析函数之间的关系。
。我们称此为模柯西–黎曼方程(简称模C.-R.方程)。进一步,我们给出了模解析的充分必要条件:(1) u(x,y) ,v(x,y) 在区域D 内满足模C.-R.方程;(2)u(x,y) ,v(x,y) 在区域 D内满足uxuy=-vxvy 。最后,我们讨论了模解析函数与已有的各类复变函数,如解析函数,半解析函数,共轭解析函数之间的关系。
Abstract:
In this paper, the finite number
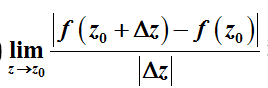
is called the module derivative of complex function
f(z) . And if
f(z) exists module derivative at any
z0 point of some field D, then
f(z) is module analytic function over field D . Let
f(z)=u(x,y)+iv(x,y) be a complex function, then we give a necessary condition, such that
f(z) is a module analytic function as follows:
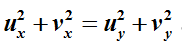
which can be called module Cauchy-Riemann equation or shortly by M-C.R. equation. Furthermore, for module analytic function
f(z)=u(x,y)+iv(x,y) of field D , we get the necessary and sufficient conditions: (1)
u(x,y) ,v(x,y) satisfies the M-C.R. equation within the field D. (2)
u(x,y) ,v(x,y) satisfies the equation
uxuy=-vxvy within the field D. Finally, the correlations between module analytic function and several preexisting functions are discussed, including analysis function, semi-analytic function, and conjugate analytic function.
1. 模解析函数
定义1.1:设函数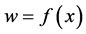 在点
在点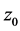 的邻域内或包含
的邻域内或包含 的区域D内有定义,如果当
的区域D内有定义,如果当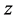 按任意方式趋于
按任意方式趋于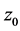 时,即当
时,即当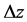 按任意方式趋于零时,比值
按任意方式趋于零时,比值
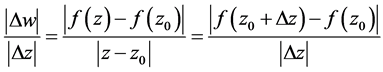 ,
, 
的极限都存在(有限),则称此极限为函数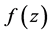 在点
在点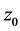 的模导数(记为
的模导数(记为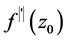 ),此时称函数
),此时称函数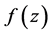 于点
于点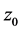 模可导。若
模可导。若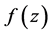 在
在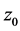 的某个邻域内的任一点模可导,则称
的某个邻域内的任一点模可导,则称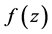 在
在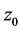 模解析。如果函数
模解析。如果函数 在区域D内任一点模解析,则称
在区域D内任一点模解析,则称 为区域D内模解析函数。或称
为区域D内模解析函数。或称 在区域D内模解析。
在区域D内模解析。
例1.1:试证明函数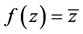 在
在 平面上不解析,但是在
平面上不解析,但是在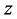 平面上模解析。
平面上模解析。
证明:由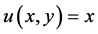 ,
,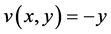 ,得
,得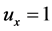 ,
,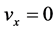 ,
,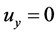 ,
,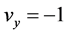 。又
。又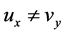 ,即此函数
,即此函数
不满足C.-R.方程,在 平面上不解析。但
平面上不解析。但
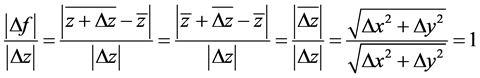
即

因此,函数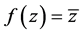 在
在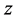 平面上处处模解析。
平面上处处模解析。
例1.2:试证明函数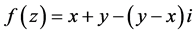 在
在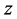 平面上不解析,但是在
平面上不解析,但是在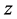 平面上模解析。
平面上模解析。
证明:由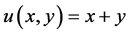 ,
,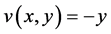 ,得
,得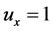 ,
, ,
,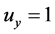 ,
,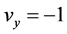 。又
。又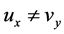 ,即此函数
,即此函数
不适合C.-R.方程,在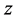 平面上不解析。但
平面上不解析。但

即

因此,函数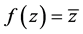 在
在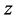 平面上处处模解析。
平面上处处模解析。
2. 主要定理及证明
如果函数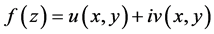 是模可微的,它的实部
是模可微的,它的实部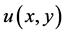 与虚部
与虚部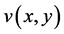 应当不是互相独立的,而必须适合一定的条件,类似于解析函数柯西–黎曼方程,我们也可以探讨这种条件。
应当不是互相独立的,而必须适合一定的条件,类似于解析函数柯西–黎曼方程,我们也可以探讨这种条件。
若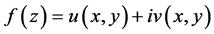 在点
在点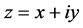 模可微,即
模可微,即
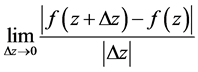 (1)
(1)
存在,设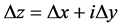 ,
,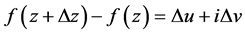 ,其中:
,其中:
 ,
,
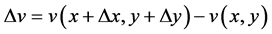 ,
,
代入,则(1)可以改写为
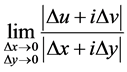 (2)
(2)
存在,因为当 无论按什么方式趋于零时,(2)总是成立的。不妨设
无论按什么方式趋于零时,(2)总是成立的。不妨设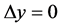 ,
,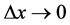 ,即变点
,即变点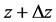 沿平行于实轴的方向趋于点
沿平行于实轴的方向趋于点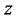 (见图1),此时有
(见图1),此时有
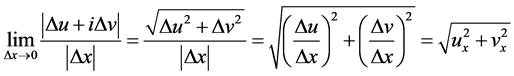 (3)
(3)
成立。同样,不妨设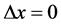 ,
, ,即变点
,即变点 沿
沿
平行于虚轴的方向趋于点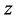 ,此时有
,此时有
 , (4)
, (4)
成立。综合(3)和(4)得
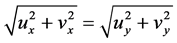 或者
或者 (5)
(5)
我们称(5)为模柯西–黎曼方程(简记为模C.-R.方程)。
由以上的讨论可以得到如下定理:
定理2.1:(模解析的必要条件)设函数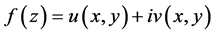 在区域
在区域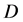 内有定义,且在
内有定义,且在 内模解析,则必有:
内模解析,则必有:
(1) 偏导数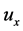 ,
, ,
,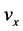 ,
, 在区域
在区域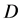 内存在;
内存在;
(2)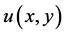 ,
, 在区域
在区域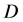 内满足模C.-R.方程。
内满足模C.-R.方程。
例2.1:试证明函数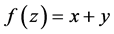 在
在 平面上满足定理2.1中的条件,但在
平面上满足定理2.1中的条件,但在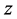 平面上不是模解析函数。
平面上不是模解析函数。
证明:因为 ,
,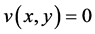 ,易知
,易知 和
和 都是可微函数。易得
都是可微函数。易得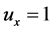 ,
,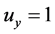 ,
,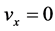 ,
, 。可知
。可知 和
和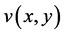 的偏导数在区域
的偏导数在区域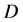 内存在,满足
内存在,满足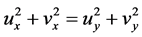 ,所以适合模C.-R.方程。但
,所以适合模C.-R.方程。但
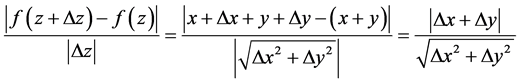
在 时极限不存在。这只要让
时极限不存在。这只要让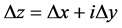 沿射线
沿射线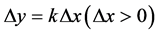 随
随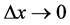 而趋于零,即知上述比值是一个与
而趋于零,即知上述比值是一个与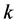 有关的值,即
有关的值,即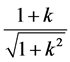 。所以函数
。所以函数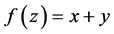 在
在 平面上不是模解析函数。下面我们给出判定一个复变函数是否模解析的充要条件:
平面上不是模解析函数。下面我们给出判定一个复变函数是否模解析的充要条件:
定理2.2:(模解析的充要条件)设函数 在区域
在区域 内有定义,其在区域
内有定义,其在区域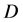 内模解析的充分必要条件是:
内模解析的充分必要条件是:
(1)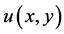 ,
,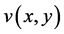 在区域
在区域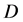 内满足模
内满足模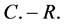 方程;
方程;
(2) 偏导数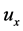 ,
, ,
,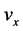 ,
,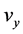 在区域
在区域 内存在且
内存在且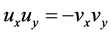 。
。
证明:设函数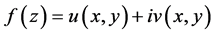 ,由极坐标变换
,由极坐标变换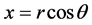 ,
, ,
, ,于是对任意
,于是对任意 ,有
,有 ,上式表明
,上式表明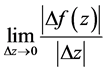 与
与 的取值无关。
的取值无关。

由于此极限与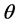 的取值无关,即函数
的取值无关,即函数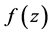 在区域
在区域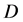 内模解析充要条件为
内模解析充要条件为
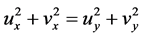 且
且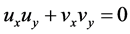 .
.
综上,定理2.2得证。
例2.2:试证明函数 在
在 平面上模解析。
平面上模解析。
证明:令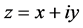 ,于是
,于是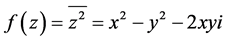 ,易得
,易得
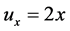 ,
, ,
,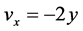 ,
, .
.
满足 ,且
,且 ,适合模C.-R.方程,由定理2.2知
,适合模C.-R.方程,由定理2.2知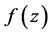 在
在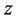 平面上模解析,并且
平面上模解析,并且
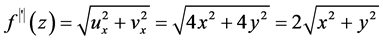 .
.
例2.3:讨论函数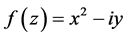 的模解析性。
的模解析性。
解:因为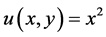 ,
,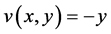 ,故:
,故:
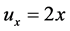 ,
,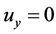 ,
, ,
,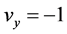 ,
,
满足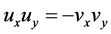 ,若要
,若要 ,须
,须 。故仅在直线
。故仅在直线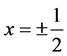 上满足模C.-R.方程,从而仅在直线
上满足模C.-R.方程,从而仅在直线 上
上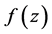 模可导,但在
模可导,但在 平面上,
平面上,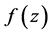 却处处不模解析。
却处处不模解析。
3. 模解析函数与其它函数类的关系
定理3.1解析函数一定是模解析函数,模解析函数不一定是解析函数。
证明:设函数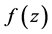 是在区域
是在区域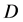 内是解析函数,若任一点
内是解析函数,若任一点 ,则
,则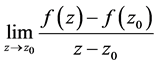 存在,必有
存在,必有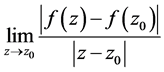 极限存在,于是函数
极限存在,于是函数 在区域
在区域 内模解析。所以解析函数一定是模解析函数。反之,模解析函数不一定是解析函数。
内模解析。所以解析函数一定是模解析函数。反之,模解析函数不一定是解析函数。
例3.1:函数 在
在 平面上模解析,但在
平面上模解析,但在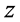 平面上不是解析函数。
平面上不是解析函数。
例3.2:函数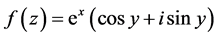 在
在 平面上是模解析也是解析函数。
平面上是模解析也是解析函数。
证明:因 ,于是有
,于是有
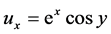 ,
, ,
,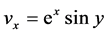 ,
,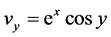 .
.
适合 且
且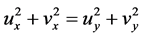 ,满足定理2.2中的条件,所以
,满足定理2.2中的条件,所以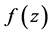 在
在 平面上是模解析函数,其在
平面上是模解析函数,其在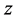 平面上也是解析函数。
平面上也是解析函数。
文献 [1] 给出了半解析函数的定义如下:假定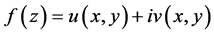 在区域
在区域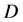 内连续,若对于每一点
内连续,若对于每一点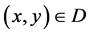 ,都有
,都有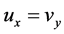 ,则称
,则称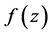 在
在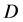 内是第一类半解析函数;若对于每一点
内是第一类半解析函数;若对于每一点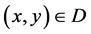 ,都有
,都有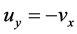 ,则称
,则称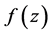 在
在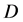 内是第二类半解析函数,第一类半解析函数和第二类半解析函数统称为半解析函数 [1] 。
内是第二类半解析函数,第一类半解析函数和第二类半解析函数统称为半解析函数 [1] 。
定理3.2:模解析函数不一定是半解析函数,半解析函数也不一定是模解析函数。
证明:模解析函数的条件 且
且 与半解析函数的条件
与半解析函数的条件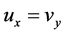 或者
或者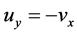 进行比较即可的定理结论。
进行比较即可的定理结论。
例3.3:函数 在
在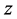 平面上是模解析函数,但不是半解析函数。
平面上是模解析函数,但不是半解析函数。
证明:由例2.2知,函数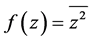 是模解析函数,令
是模解析函数,令 ,于是
,于是
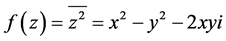 ,
,
易得
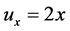 ,
, ,
, ,
,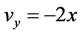 .
.
 ,
,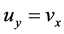 。根据半解析函数的定义,得
。根据半解析函数的定义,得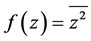 不是半解析函数。
不是半解析函数。
例3.4:函数 在
在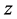 平面上是半解析函数,但不是模解析函数。
平面上是半解析函数,但不是模解析函数。
证明:因 ,则
,则 ,
,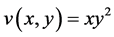 。易得
。易得
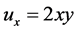 ,
,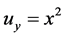 ,
,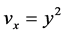 ,
, .
.
于是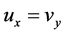 ,根据半解析函数的定义,所以
,根据半解析函数的定义,所以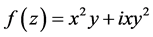 是半解析函数,但
是半解析函数,但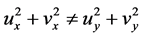 ,所以根据定理2.2知
,所以根据定理2.2知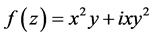 不是模解析函数。
不是模解析函数。
文献 [2] 给出了共轭解析函数的充要条件如下:
(1) 二元函数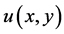 ,
, 在区域
在区域 内可微;
内可微;
(2)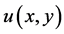 ,
, 在区域
在区域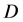 内满足共轭解析条件:
内满足共轭解析条件: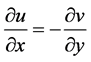 ,
,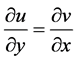 ;
;
则(1)和(2)称为函数 在区域
在区域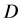 内共轭解析的充分必要条件 [2] 。
内共轭解析的充分必要条件 [2] 。
定理3.3:(共轭解析一定模解析)共轭解析函数一定是模解析函数,但模解析函数不一定是共轭解析函数。
证明:若函数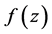 是共轭解析的,在
是共轭解析的,在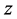 平面上则有
平面上则有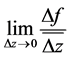 存在,所以:
存在,所以:
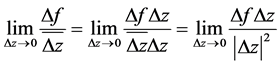
极限存在,则必有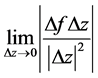 存在,易得到
存在,易得到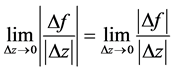 也存在,因而函数
也存在,因而函数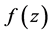 是模解析函数.所以共轭解析函数一定是模解析函数。反之,模解析函数不一定是共轭解析函数。
是模解析函数.所以共轭解析函数一定是模解析函数。反之,模解析函数不一定是共轭解析函数。
例3.5:函数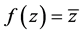 在
在 平面上模解析,同时也是共轭解析函数。
平面上模解析,同时也是共轭解析函数。
证明:由例2.1知 是模解析函数,令
是模解析函数,令 ,可得
,可得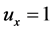 ,
,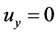 ,
,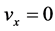 ,
,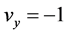 ,因而满足共轭解析条件
,因而满足共轭解析条件 ,
, 。所以函数
。所以函数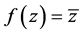 在
在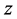 平面上共轭解析。
平面上共轭解析。
例3.6:函数 在
在 平面上是模解析函数,但不是共轭解析函数。
平面上是模解析函数,但不是共轭解析函数。
证明:函数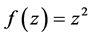 ,令
,令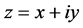 ,得
,得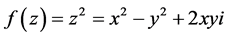 ,于是得
,于是得
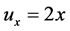 ,
, ,
,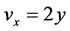 ,
,
满足 且
且 ,根据定理3.2知
,根据定理3.2知 是模解析函数,但不满足
是模解析函数,但不满足 ,
,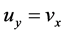 ,不适合共轭解析条件,所以此函数不是共轭解析函数。
,不适合共轭解析条件,所以此函数不是共轭解析函数。
定理3.4:函数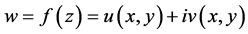 既是共轭解析也是半解析函数必须满足下面条件之一:(1)
既是共轭解析也是半解析函数必须满足下面条件之一:(1)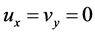 。(2)
。(2)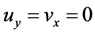 。
。
证明:设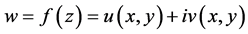 是共轭解析函数,则
是共轭解析函数,则 且
且 。
。
若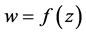 是第一类半解析函数,则
是第一类半解析函数,则 ,所以有
,所以有 且
且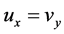 ,于是
,于是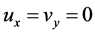 。
。

Figure 2. The diagram of inclusion relation
图2. 包含关系图
若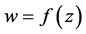 是第二类半解析函数,则
是第二类半解析函数,则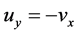 ,所以有
,所以有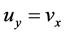 且
且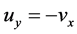 ,于是
,于是 。
。
推论3.1:模解析函数与解析函数,半解析函数,共轭解析函数的包含关系,如图2所示。
本文所涉及到基本概念和已知结论在参考文献 [2] [3] [4] [5] [6] 里。