摘要: 通过运用一类含参数的
G 展开法对RLW-Burgers方程进行了研究,求得了该方程的多种函数形式的新显式行波解。事实证明,此类含参数的
G 展开法不仅可以得到非线性偏微分方程的精确解,而且由于所含参数的任意性,可以得到非线性偏微分方程更多类型的显式行波解。
Abstract:
We studied the RLW-Burgers equation by using a class of parametric G expansion method, and obtained many new explicit traveling wave solutions for the various functional forms of the equa-tion. In fact, the parameters of the G expansion method can not only obtain the exact solutions of nonlinear partial differential equations, but also because of the arbitrariness of parameters, we can obtain more explicit traveling wave solutions for nonlinear partial differential equations.
1. 引言
求解非线性偏微分方程,尤其是求得非线性偏微分方程的精确解是当前非线性问题研究的关键。近年来,已经出现了许多求解非线性偏微分方程精确解的方法,例如Backlund变换法、Jacobi椭圆函数展开法、tanh函数展开法、变量分离法、首次积分法等等。近期,由文献 [1] 提出的 展开法,是通过假设非线性偏微分方程的解可以由一类线性常微分方程的解来表示的一种简单有效的求解非线性偏微分方程显式行波解的方法。
展开法,是通过假设非线性偏微分方程的解可以由一类线性常微分方程的解来表示的一种简单有效的求解非线性偏微分方程显式行波解的方法。
考虑可以描述河渠中水波表面传播性态的RLW-Burgers方程
 (1)
(1)
其中 。文献 [2] 和文献 [3] 研究了该方程行波解的存在性及行波解的性质;文献 [4] 得到了该方程的振荡激波解;文献 [5] 通过未知函数的变换及待定系数法得到了方程的显式行波解;文献 [6] 研究了该方程的古典对称和势对称,并利用推广的Tanh函数法和Lie变换群得到了该方程的一系列精确解。
。文献 [2] 和文献 [3] 研究了该方程行波解的存在性及行波解的性质;文献 [4] 得到了该方程的振荡激波解;文献 [5] 通过未知函数的变换及待定系数法得到了方程的显式行波解;文献 [6] 研究了该方程的古典对称和势对称,并利用推广的Tanh函数法和Lie变换群得到了该方程的一系列精确解。
本文借由 展开法的基本思想 [7] [8] [9] [10] [11] ,构造了一类含参数的
展开法的基本思想 [7] [8] [9] [10] [11] ,构造了一类含参数的 展开法,即假设非线
展开法,即假设非线
性偏微分方程的解具有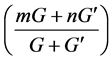 的多项式的形式,其中
的多项式的形式,其中 为任意不等的自由参数,
为任意不等的自由参数, 是由一类非线
是由一类非线
性的常微分方程的显式行波解得到。运用此类展开法,得到了RLW-Burgers方程的多种函数形式的新显式行波解。
2. 含参数的G展开法
将非线性偏微分方程
 (2)
(2)
作行波变换,令 ,
, ,则上式化为常微分方程
,则上式化为常微分方程
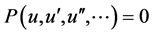 (3)
(3)
设方程(2)的解为
 (4)
(4)
其中 为自由参数,
为自由参数, 为待定的常数,通过齐次平衡法可以确定参数
为待定的常数,通过齐次平衡法可以确定参数 ;并且要求其中的
;并且要求其中的 满足一类非线性的常微分方程
满足一类非线性的常微分方程
 (5)
(5)
这里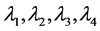 为任意的常数。
为任意的常数。
对于方程(5)式,通过借助符号计算软件Mathematica,我们得到了其以下几种情况下的解:
① 当 且
且 时,方程(5)的解为
时,方程(5)的解为
 (6)
(6)
这里 为积分常数。
为积分常数。
② 当 且
且 时,方程(5)的解为
时,方程(5)的解为
 (7)
(7)
这里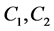 为积分常数。
为积分常数。
③ 当 且
且 时,方程(5)的解为
时,方程(5)的解为
 (8)
(8)
这里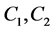 为积分常数。
为积分常数。
④ 当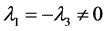 且
且 时,方程(5)的解为
时,方程(5)的解为
 (9)
(9)
这里 为积分常数。
为积分常数。
⑤ 当 且
且 时,方程(5)的解为
时,方程(5)的解为
 (10)
(10)
这里 为积分常数。
为积分常数。
3. RLW-Burgers方程的新显式行波解
设方程(1)有行波解 ,其中
,其中 是一非零常数,从而方程(1)化为
是一非零常数,从而方程(1)化为
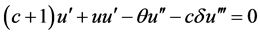
对其两边进行积分,并取积分常数为零,可得
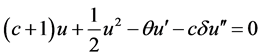 (11)
(11)
设方程(1)的解为 ,且
,且 满足方程
满足方程

这里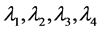 为任意常数。利用齐次平衡法,有
为任意常数。利用齐次平衡法,有 ,可得
,可得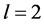 ,则方程(1)的解表示为
,则方程(1)的解表示为
 (12)
(12)
由上式可以求得 的各阶导数,再结合方程(5)式,我们得到,
的各阶导数,再结合方程(5)式,我们得到,


将上面的 及
及 分别代入(11)式,合并
分别代入(11)式,合并 的同幂次项,并令其各次幂的系数为零,我们得到
的同幂次项,并令其各次幂的系数为零,我们得到
 :
: 
 :
: 
 :
: 
 :
: 
 :
: 
由此我们得到了关于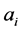 的代数方程组,通过借助符号计算软件
的代数方程组,通过借助符号计算软件 ,可得
,可得




这里 。将上面得到的
。将上面得到的 代入(12)式,并结合方程(5)式的解
代入(12)式,并结合方程(5)式的解 ,我们得到了方程(1)式的下列显式行波解:
,我们得到了方程(1)式的下列显式行波解:
① 当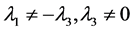 且
且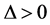 时,
时, ,由(6)式,可得方程(1)的解为
,由(6)式,可得方程(1)的解为

此为方程的三角函数形式的解。
② 当 ,
, 且
且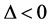 时,
时, ,由(7)式,可得方程(1)的解为
,由(7)式,可得方程(1)的解为

此为方程的双曲函数形式的解。
③ 当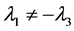 且
且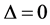 时,
时, ,由(8)式,可得方程(1)的解为
,由(8)式,可得方程(1)的解为
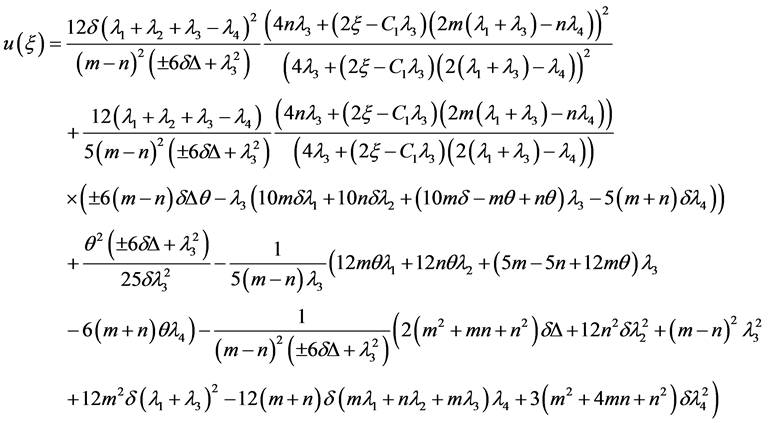
此为方程的有理函数形式的解。
④ 当 且
且 时,
时, ,由(9)式,可得方程(1)的解为
,由(9)式,可得方程(1)的解为

此为方程的指数函数形式的解。
⑤ 当 且
且 时,
时, ,由(10)式,可得方程(1)的解为
,由(10)式,可得方程(1)的解为

此为方程的另一有理函数形式的解。
4. 总结
本文构造了一类含有自由参数 的
的 形式的展开法,并用其对RLW-Burgers方程进行
形式的展开法,并用其对RLW-Burgers方程进行
了求解,得到了该方程的三角函数形式、双曲函数形式、指数函数形式和有理函数形式的新显式行波解。由此可见,此类含参数的G展开法不仅是求解非线性偏微分方程的有效方法,而且对于可以自由选取的参数,我们可以得到非线性偏微分方程更多类型的显式精确解。
基金项目
国家自然科学基金(11601109),海南省自然科学基金(117066)。