1. 引言
n阶一般线性群是由n阶可逆矩阵组成的群,矩阵的元素取自R群运算,为通常的矩阵乘法,记为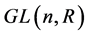 ;特殊线性群是
;特殊线性群是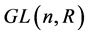 中行列式为1的全体矩阵,它们对于矩阵乘法构成
中行列式为1的全体矩阵,它们对于矩阵乘法构成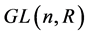 的一个子群,记为
的一个子群,记为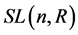 。一般线性群
。一般线性群 和特殊线性群
和特殊线性群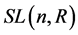 都是经典的李群,它们与群论和几何的研究有着密切的联系,在几何分析中有如下深刻的结果:特殊线性群
都是经典的李群,它们与群论和几何的研究有着密切的联系,在几何分析中有如下深刻的结果:特殊线性群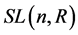 的有限Abelian子群是紧黎曼曲面的微分同胚不变量。这一结论将几何和代数(群理论)紧密联系起来,本文以此为出发点,结合群理论中对有限Abel群结构的完整刻画,如:有限Abel群可以分解成阶为素数的方幂的循环群(循环p-群)的直积 [1] 等,对特殊线性群
的有限Abelian子群是紧黎曼曲面的微分同胚不变量。这一结论将几何和代数(群理论)紧密联系起来,本文以此为出发点,结合群理论中对有限Abel群结构的完整刻画,如:有限Abel群可以分解成阶为素数的方幂的循环群(循环p-群)的直积 [1] 等,对特殊线性群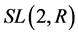 的有限Abelian子群进行研究,从而进一步加深对紧黎曼曲面的认识。
的有限Abelian子群进行研究,从而进一步加深对紧黎曼曲面的认识。
2. 基本概念、定理和方法
2.1. 基本概念和定理
下面列出一些与群和矩阵相关的概念和定理(可参考文献 [1] [2] ),方便后面章节使用。
定义2.1.1 [1] 设G为非空集合,“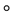 ”为G上的一个代数运算,若G的运算满足:
”为G上的一个代数运算,若G的运算满足:
1) “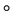 ”满足结合律,即
”满足结合律,即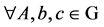 ,都有
,都有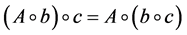 ;
;
2) G中有元素e,使对每个元 ,有
,有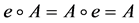 ;
;
3) 对G中每个元素A,存在元素 ,使得
,使得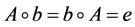 。
。
则G关于运算“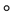 ”构成一个群(Group),记为
”构成一个群(Group),记为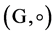 ,在不产生混淆的前提下,简记为G。
,在不产生混淆的前提下,简记为G。
定义2.1.2 [1] 如果对群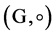 中任两个元素A,b均有
中任两个元素A,b均有
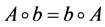 ,
,
即G的代数运算满足交换律,则称G为交换群(commutative Group)或Abel群(Abelian Group)。
定义2.1.3 [1] 群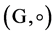 中的元素个数叫做群G的阶(order),记为
中的元素个数叫做群G的阶(order),记为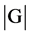 。如果
。如果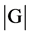 有限,称G为有限群(Finite Group),特别地,当
有限,称G为有限群(Finite Group),特别地,当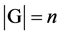 时,称G为n阶群,否则称G为无限群(infinite Group)。
时,称G为n阶群,否则称G为无限群(infinite Group)。
定义2.1.4 [1] 设G为群,H是G的一个非空子集,如果H关于G的运算也构成群,则称H为G的一个子群(subgroup),记作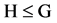 。
。
定义2.1.5 [1] 元素在实数域r中全体n阶可逆矩阵对于矩阵的乘法构成一个群,这个群记为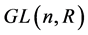 ,称为n阶一般线性群,
,称为n阶一般线性群,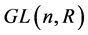 中全体行列式为1的矩阵对于矩阵的乘法也构成一个群,这个群记为
中全体行列式为1的矩阵对于矩阵的乘法也构成一个群,这个群记为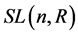 ,称为n阶特殊线性群。特别地,当n = 2时有
,称为n阶特殊线性群。特别地,当n = 2时有
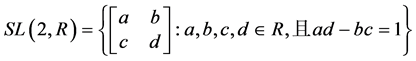 .
.
定义2.1.6 [1] 设G为群,如果存在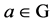 时
时
 ,
,
则称G为循环群,并称A是群G的一个生成元(Generator)。习惯上记为 ,当G中的元素个数是无限时,称G为无限循环群;当G中元素的个数为n时,称G为n阶循环群。
,当G中的元素个数是无限时,称G为无限循环群;当G中元素的个数为n时,称G为n阶循环群。
定义2.1.7 [1] 一般地,我们称下列形式矩阵为多项式矩阵,或l-矩阵:
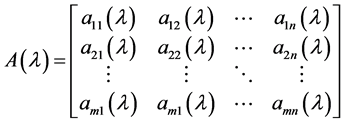
其中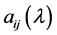 是以
是以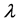 为未定元的数域k上的多项式。l-矩阵的加法、数乘及乘法与数域上的矩阵运算一样,只需在运算过程中将数的运算代之以多项式运算即可。
为未定元的数域k上的多项式。l-矩阵的加法、数乘及乘法与数域上的矩阵运算一样,只需在运算过程中将数的运算代之以多项式运算即可。
定义2.1.8 [2] 设 是一个n阶l-矩阵,k是小于等于n的某个自然数。如果
是一个n阶l-矩阵,k是小于等于n的某个自然数。如果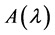 的所有k阶子式的最大公因子(它是首一多项式)不等于零,则称这个多项式为
的所有k阶子式的最大公因子(它是首一多项式)不等于零,则称这个多项式为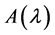 的k阶行列式因子,记为
的k阶行列式因子,记为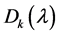 ,若
,若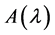 的所有k阶子式都等于零,则规定
的所有k阶子式都等于零,则规定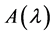 的k阶行列式因子等于零。
的k阶行列式因子等于零。
定义2.1.9 [2] 设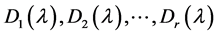 是l-矩阵
是l-矩阵 的非零行列式因子,则
的非零行列式因子,则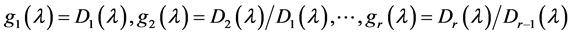 称为
称为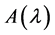 的不变因子。
的不变因子。
定义2.1.10 [2] 若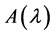 ,
,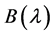 都是
都是 矩阵且
矩阵且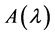 经过初等变换后可变为
经过初等变换后可变为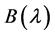 ,则称
,则称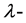 矩阵
矩阵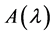 与
与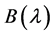 相抵。
相抵。
定理2.1.1 [2] 设A是数域k上的n阶矩阵,则A的特征矩阵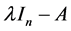 必相抵于
必相抵于
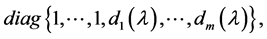
其中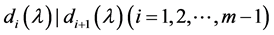 。
。
定理2.1.2 [2] 下列r阶矩阵
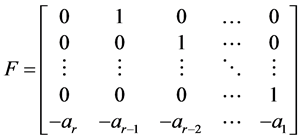
的行列式因子等于
 ,
,
其中共有r − 1个1,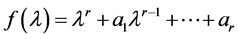 ,F的不变因子组也由
,F的不变因子组也由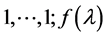 给出。
给出。
定理2.1.3 [2] 设A是数域k上的n阶方阵,A的不变因子组为
 ,
,
其中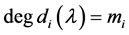 ,则A相似于下列分块对角矩阵:
,则A相似于下列分块对角矩阵:
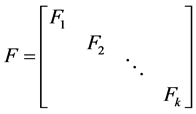
其中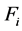 的阶等于
的阶等于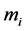 ,且
,且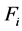 是形如定理2.1.2的矩阵,
是形如定理2.1.2的矩阵, 的最后一行由
的最后一行由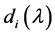 系数(除最高次项)的负值组成。
系数(除最高次项)的负值组成。
2.2. 常系数线性齐次递归关系的求解方法 [3]
本节我们介绍常系数线性齐次递归关系的求解,相关内容请参考文献 [3] 。
常系数线性齐次递归关系,其形如
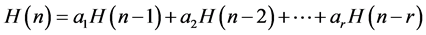
或
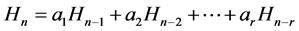 (2.2.1)
(2.2.1)
这里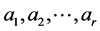 全部是常系数。例如
全部是常系数。例如
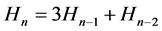
就是一个常系数线性齐次递归方程。假定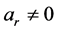 ,则递归关系(2.2.1)称为是r阶的。为了不失一般性,如果序列中r个相邻的H值
,则递归关系(2.2.1)称为是r阶的。为了不失一般性,如果序列中r个相邻的H值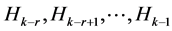 对某一k已知,则可用(2.2.1)算出
对某一k已知,则可用(2.2.1)算出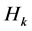 的值,于是
的值,于是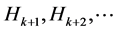 的值也可递归地算出。这就推出,(2.2.1)的解唯一地由r个相邻的H值(边界条件)所决定。因此,(2.2.1)的解的一般形式包含有r个待定常数,这些常数可由序列中相邻的r个H值来决定。我们把(2.2.1)改写成如下形式
的值也可递归地算出。这就推出,(2.2.1)的解唯一地由r个相邻的H值(边界条件)所决定。因此,(2.2.1)的解的一般形式包含有r个待定常数,这些常数可由序列中相邻的r个H值来决定。我们把(2.2.1)改写成如下形式
 (2.2.2)
(2.2.2)
这里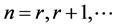 。
。
我们把与递归关系(2.2.1)或(2.2.2)相联系的方程
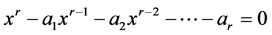 (2.2.3)
(2.2.3)
称为(2.2.1)或(2.2.2)的特征方程。方程(2.2.3)有r个根 ,这些根称为方程(2.2.1)的特征根。因为
,这些根称为方程(2.2.1)的特征根。因为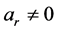 ,这些特征根必定全不为零。这些根可能是互异的,也可能有重根,还有可能是复根。关于常系数线性齐次递归关系的求解如下:
,这些特征根必定全不为零。这些根可能是互异的,也可能有重根,还有可能是复根。关于常系数线性齐次递归关系的求解如下:
1) 若特征方程有r个不同的特征根
定理设递归关系
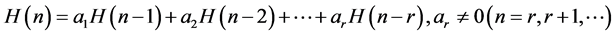 的特征根
的特征根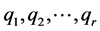 互不相同,则
互不相同,则
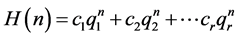
是一般解。
2) 若特征方程有重根
定理设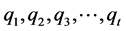 是递归关系
是递归关系
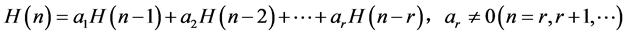
的特征方程互异的根。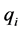 是特征方程的
是特征方程的 重根
重根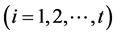 ,那么这个递归关系对应
,那么这个递归关系对应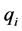 部分的一般解是
部分的一般解是
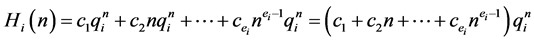
而这个递归关系的一般解是
 .
.
3) 若特征方程出现复根
当特征方程的诸系数是实数,但某些特征根是复数时,齐次解则写成另一种形式。因为复数根总是成对出现的,故设
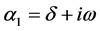 ,
, 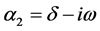
是一对共轭复根,则对应的齐次解为
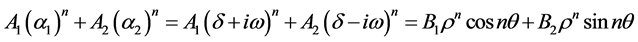
其中,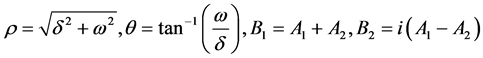
注意,这里的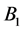 和
和 是由边界条件决定的常数。
是由边界条件决定的常数。
3. SL(2, R)的有限Abelian子群的结构
由群理论相关的结论我们有:有限循环群一定是有限Abelian群,故我们可以先寻找到特殊线性群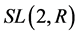 的有限循环子群,即对任意的
的有限循环子群,即对任意的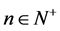 ,我们需要找到所有满足条件
,我们需要找到所有满足条件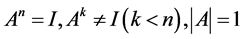 的矩阵。
的矩阵。
3.1. 特殊例子的讨论
由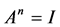 ,知A的特征根满足
,知A的特征根满足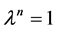 ,其特征根集为
,其特征根集为
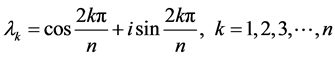 . [4]
. [4]
(此处A的特征根解集参考文献 [4] )
特别地,就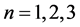 我们有如下的结论:
我们有如下的结论:
1) 当n=1时,若要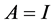 ,则A为单位阵;
,则A为单位阵;
2) 当n=2时,若要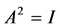 ,
,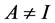 且
且 ,则此时无解。分析如下:
,则此时无解。分析如下:
① 考虑特征值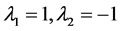 ,A特征多项式为
,A特征多项式为 ,
,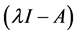 的2阶行列式因子就是矩阵A的特征多项式
的2阶行列式因子就是矩阵A的特征多项式 ,由定理2.1.1可以得到
,由定理2.1.1可以得到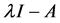 相抵于
相抵于 ,矩阵A的不变因子为
,矩阵A的不变因子为
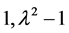 .
.
于是,由定理2.1.3,矩阵A的有理标准型为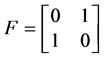 ,即
,即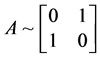 ,此时
,此时 ,不符合
,不符合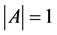 之要求。
之要求。
② 考虑特征值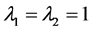 ,其特征多项式为
,其特征多项式为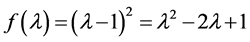 ,
,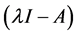 的2阶行列式因子就是矩阵A的特征多项式
的2阶行列式因子就是矩阵A的特征多项式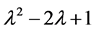 ,于是由定理2.1.1可以得到
,于是由定理2.1.1可以得到 相抵于
相抵于 ,矩阵A的不变因子为
,矩阵A的不变因子为
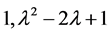 .
.
由定理2.1.3,矩阵A的有理标准型为 ,即
,即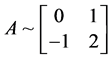 ,此时
,此时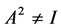 ,也不符合要求。
,也不符合要求。
③ 考虑特征值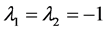 ,其特征多项式为
,其特征多项式为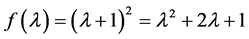 ,
,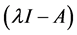 的2阶行列式因子就是矩阵A的特征多项式为
的2阶行列式因子就是矩阵A的特征多项式为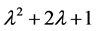 ,由定理2.1.1可以得到
,由定理2.1.1可以得到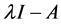 相抵于
相抵于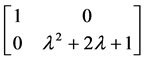 ,矩阵A的不变因子为
,矩阵A的不变因子为
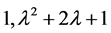 .
.
由定理2.1.3,矩阵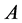 的有理标准型为
的有理标准型为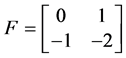 ,即
,即 ,此时
,此时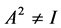 ,也不符合要求。
,也不符合要求。
3) 当n = 3时,要求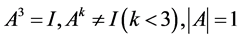 ,此时有解
,此时有解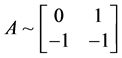 。分析如下:
。分析如下:
由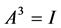 知矩阵A的特征值为
知矩阵A的特征值为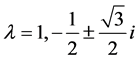
① 当 时,讨论的情况与
时,讨论的情况与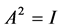 相同,可知此时无解。
相同,可知此时无解。
② 当 时(复根成对出现,相互共轭),A的特征多项式为
时(复根成对出现,相互共轭),A的特征多项式为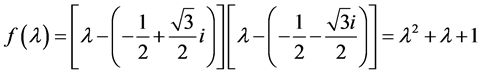 ,
,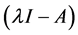 的2阶行列式因子就是矩阵A的特征多项式
的2阶行列式因子就是矩阵A的特征多项式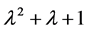 ,由定理2.1.1可以得到
,由定理2.1.1可以得到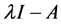 相抵于
相抵于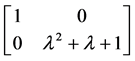 ,矩阵A的不变因子为
,矩阵A的不变因子为
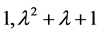
由定理2.1.3,矩阵A的有理标准型为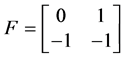 ,即
,即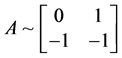 ,满足条件
,满足条件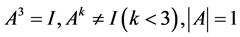 ,为我们所求的解。
,为我们所求的解。
3.2. 一般形式的归纳和证明
3.2.1. 一般情形的讨论
下面考虑 的情形。通过对
的情形。通过对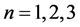 的特殊情形进行的讨论,我们发现一般情形下的讨论可以类似的进行,主要从特征根(复根成共轭对)入手,结合相关的定理(定理2.1.1、定理2.1.3),通过解常系数线性齐次递归方程最终给出一般情形下的结果。
的特殊情形进行的讨论,我们发现一般情形下的讨论可以类似的进行,主要从特征根(复根成共轭对)入手,结合相关的定理(定理2.1.1、定理2.1.3),通过解常系数线性齐次递归方程最终给出一般情形下的结果。
考虑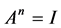 (
(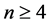 ),此时若A存在一组共轭特征根
),此时若A存在一组共轭特征根 和
和 ,这里
,这里  (若
(若 为偶数,则
为偶数,则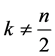 ),则A的特征多项式为
),则A的特征多项式为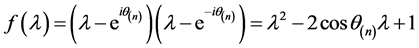 ,
,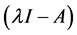 的2阶行列式因子就是A的特征多项式
的2阶行列式因子就是A的特征多项式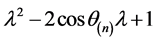 ,于是由定理2.1.1可以得到
,于是由定理2.1.1可以得到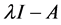 相抵于
相抵于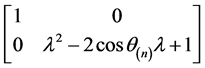 ,A的不变因子为
,A的不变因子为
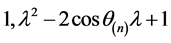 .
.
由定理2.1.3,A的有理标准型为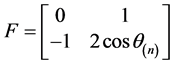 ,即
,即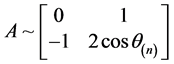 ,此时有
,此时有 ,由前面的讨论我们知道,若能证明F满足
,由前面的讨论我们知道,若能证明F满足 ,则可以得到
,则可以得到 。
。
3.2.2. 的证明
的证明
证明:由于矩阵A的特征多项式为 ,而
,而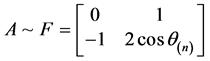 ,故
,故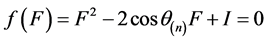 ,即
,即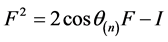 ,不妨令
,不妨令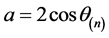 ,则:
,则:
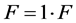 (1)
(1)
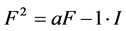 , (2)
, (2)
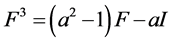 , (3)
, (3)
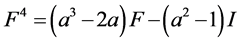 , (4)
, (4)
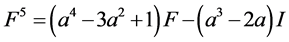 , (5)
, (5)
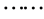
经过观察我们发现,等式(2)中F的系数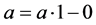 ,等式(3)中F的系数
,等式(3)中F的系数 ,等式(4)中F的系数
,等式(4)中F的系数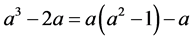 ,等式(5)中F的系数
,等式(5)中F的系数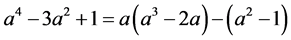 ,我们把每一等式中F的系数看成数列
,我们把每一等式中F的系数看成数列 中的元素则有:
中的元素则有: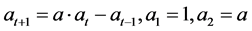 。这是一个常系数线性齐次递归方程,故根据相应的常系数线性齐次递归关系的求解方法,我们可以解得
。这是一个常系数线性齐次递归方程,故根据相应的常系数线性齐次递归关系的求解方法,我们可以解得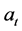 ,过程如下:
,过程如下:
由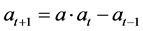 可以得到它的特征方程为
可以得到它的特征方程为
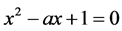 ,
,
因为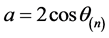 ,
,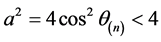 ,所以
,所以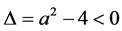 ,由常系数线性齐次递归关系可知,特征方程存在2个复根
,由常系数线性齐次递归关系可知,特征方程存在2个复根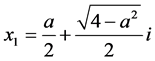 ,
,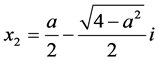 则
则
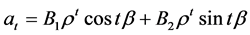 ,其中
,其中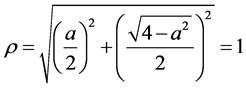 ,
,
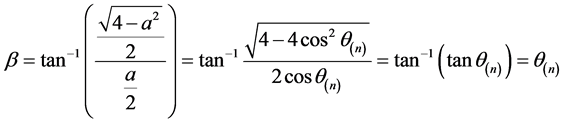 ,
,
所以 ,把
,把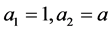 代入
代入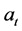 得:
得:
 ,
,
解之得:
 ,
,
故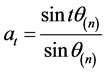 ,(
,(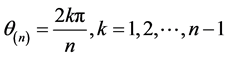 且若
且若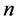 为偶数,则
为偶数,则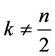 ),
),
从而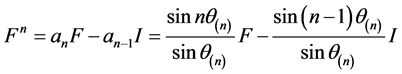 ,即有
,即有
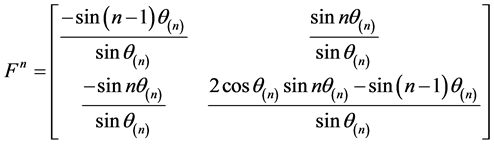 ,
,
由和差化积公式得:
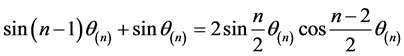 ,
,
又
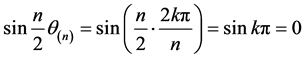 ,
,
所以
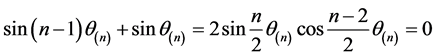 .
.
即
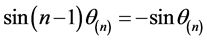 ,
,
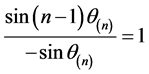 ,
,
又
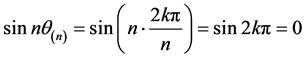 ,
,
所以
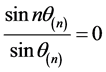 ,
,
故
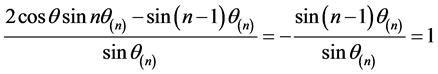 ,
,
从而 ,证毕。
,证毕。
3.2.3. SL(2, R)的有限循环子群的结构
由前面的讨论,我们已经找到了满足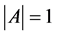 且
且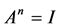 的所有矩阵,即:
的所有矩阵,即: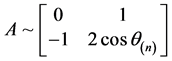 ,进一步为了在这些矩阵中找出符合条件
,进一步为了在这些矩阵中找出符合条件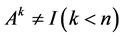 的矩阵,我们需要确定符合条件
的矩阵,我们需要确定符合条件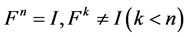 的
的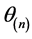 。
。
例如,当 时,
时,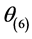 的取值为
的取值为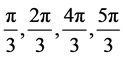 ,其中
,其中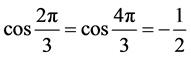 ,
,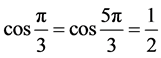 ,
,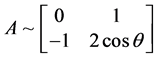 ,解得
,解得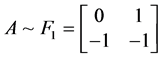 和
和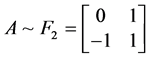 ,此时这两组解均满足
,此时这两组解均满足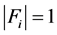 且
且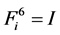 ,但对
,但对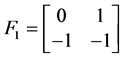 而言,有
而言,有 ,即
,即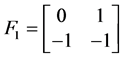 为
为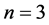 时的一个解,重复出现。下面我们找出符合条件
时的一个解,重复出现。下面我们找出符合条件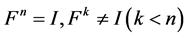 的所有
的所有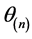 (
(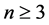 ),使得最后的结果不会重复,也不会遗漏。
),使得最后的结果不会重复,也不会遗漏。
对任意的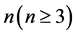 ,
,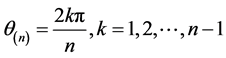 ,当k取
,当k取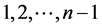 中不同的值时,
中不同的值时,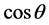 总会出现一对相同的值(仅有一对),如
总会出现一对相同的值(仅有一对),如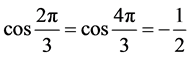 ,这是因为,若
,这是因为,若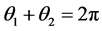 ,则
,则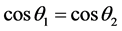 。由此我
。由此我
们可以缩小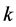 的取值范围。
的取值范围。
当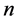 为奇数时,
为奇数时,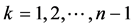 ,
,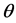 可取
可取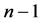 个值中,且首尾的值相加恰好等于
个值中,且首尾的值相加恰好等于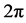 ,故我们只需取前
,故我们只需取前
面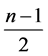 个值即可,即
个值即可,即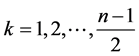 。由于n是奇数,而2k是偶数,所以
。由于n是奇数,而2k是偶数,所以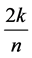 一定是一个最简分数,此时
一定是一个最简分数,此时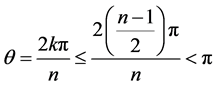 ,
,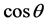 互不相等。
互不相等。
当 为偶数时,
为偶数时,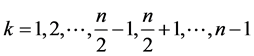 ,与前面的讨论类似,我们可以将
,与前面的讨论类似,我们可以将 的取值范围限定在前面
的取值范围限定在前面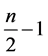 个值,即
个值,即 。进一步,由于2k是偶数时,而n也是偶数(不妨设
。进一步,由于2k是偶数时,而n也是偶数(不妨设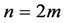 ),则有
),则有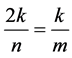 ,当k为奇数时,
,当k为奇数时, 是一个最简分数,不会导致解的重复;而当k为偶数时,由于
是一个最简分数,不会导致解的重复;而当k为偶数时,由于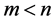 ,
,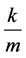 一定在前面的取值中出现过,从而导致解的重复,此时k只取
一定在前面的取值中出现过,从而导致解的重复,此时k只取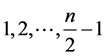 中奇数的那一部分值。
中奇数的那一部分值。
综上所述,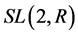 的有限Abelian子群中所有满足条件
的有限Abelian子群中所有满足条件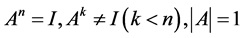 的矩阵如下:
的矩阵如下:
当n = 1时,则A为单位阵;
当n = 2时,则此时无解;
当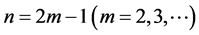 时,
时,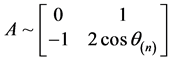 ,
,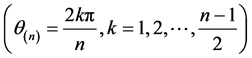 ;
;
当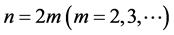 时,
时,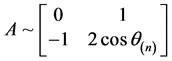 ,
,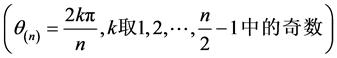 。
。
4. 进一步的问题
特殊线性群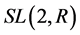 的3阶有限循环子群的生成元是
的3阶有限循环子群的生成元是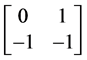 ,4阶有限循环子群的生成元是
,4阶有限循环子群的生成元是 ,5阶有限循环子群的生成元是
,5阶有限循环子群的生成元是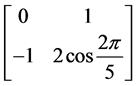 和
和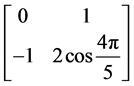 ,……,n阶有限循环子群的生成元是
,……,n阶有限循环子群的生成元是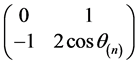 (
(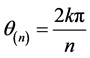 ,
, 取
取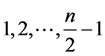 中的奇数),这些生成元所构成的循环子群能否做成特殊线性群
中的奇数),这些生成元所构成的循环子群能否做成特殊线性群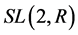 的子群的直积,目前本人还没有好的方法去解答,值得进一步探讨。
的子群的直积,目前本人还没有好的方法去解答,值得进一步探讨。