1. 引言
随着计算机技术和智能控制技术的不断发展，四旋翼飞行器因其结构简单、垂直起降和低速飞行等诸多优点，在越来越多的领域拥有广泛的应用前景。四旋翼飞行器是由4个电动桨叶组成，相邻桨叶旋转相反方向抵消扭矩。它既可以使用无线电遥控设备进行手动飞行，也可以使用远程计算机与导航设备控制进行飞行。与传统的飞行器相比，具有负载能力强、机械操作简单和作业范围广泛等优点。四旋翼飞行器采用点到点的飞行方式，包括旋进、悬停、偏航、横滚、俯仰、垂直和水平飞行。在军用和民用领域都得到广泛的应用。在军用方面主要进行侦查、监视、获取敌方情报和地面通讯等工作；在民用方面主要进行空中摄影、图像传输、交通监控、电力巡检和大气检测等工作。
目前，对于四旋翼飞行器的控制器选择，通常采用PID控制器。PID控制器作为经典的反馈控制，其有设计简单、鲁棒性强和稳定性高等优点，被应用于各种各样的生产环境。但自适应性和参数整定方面表现很差，也限制算法的发展。丁军，姚乐和杨启文等 [1] [2] [3] 采用单神经元对PID算法做出改进，并分析改进后算法的合理性。侯一民，高京都等 [4] [5] 将改进后的算法应用于实际应用中。本文采用牛顿欧拉公式建立简化的数学模型，并根据飞行器运动合力与单神经元整定PID控制器结合对加速度控制，建立姿态控制、位置控制的双闭环控制系统，实现对飞行器运动跟踪及预测，并通过simulink仿真实验，论证算法的实时性、准确性。
2. 数学模型
四旋翼飞行器是一个强耦合、非线性的欠驱动的系统，在建立数学模型之前，需要做如下假设 [6] ：
1) 机体结构完全对称，采用刚体材料；
2) 忽略地面效应对机体的影响；
3) 机体的质心与机体坐标原点重合。
地面坐标系
,，机体坐标系
，姿态角
，其中
为绕机体
轴转动的俯仰角，
，
为绕机体
轴转动的横滚角，
，
为绕机体
轴转动的偏航角，
，如图1所示。
绕
轴旋转矩阵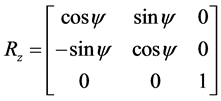
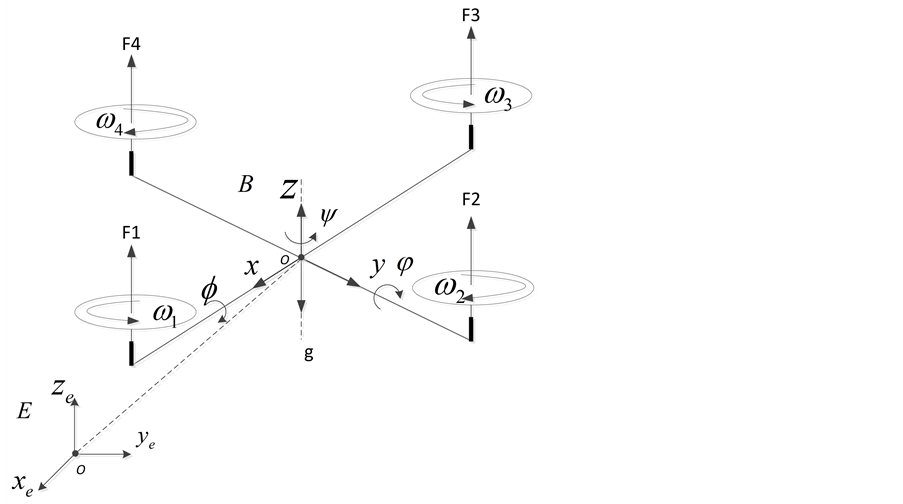
Figure 1. Mathematical modeling of quadrotor
图1. 四旋翼飞行器数学建模示意图
绕
轴旋转矩阵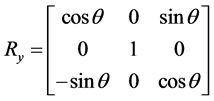
绕
轴旋转矩阵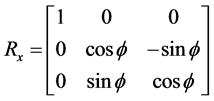
从机体坐标系到地面坐标系的旋转矩阵：
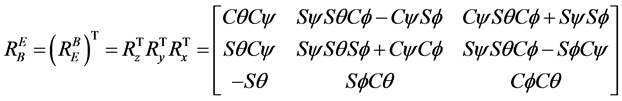
式中
。
3. 单神经元PID控制的设计
四旋翼飞行器是一个非线性系统，通过改变四个电机的转速控制飞行器的运动，机体在三维空间中的旋进运动是改变姿态角使机身俯仰、横滚或偏航提供方向和加速度，然后保持姿态角飞行器平移运动。所以在飞行控制器的设计中，首先需要计算出姿态角的大小，飞行器才能旋进运动，通常采用双闭环PID飞行控制器 [7] 。传统的PID控制器结构简单，容易实现，但自适应性不佳，收敛速度慢等缺点。单神经元PID控制器是单层网络，其计算量小、具有逼近函数的能力，弥补传统PID控制器的不足，对四旋翼飞行控制器是理想选择。
从图2可以看出，在双闭环控制器中，内环为姿态控制，外环为位置控制。当飞行控制器接收到给定的期望加速度，外环控制需要计算出飞行器需要改变姿态角，根据姿态角的变化控制飞行器飞行。内环控的输入值由外环计算出的姿态角，输出值为4个电机的转速控制飞行器的运动状态。
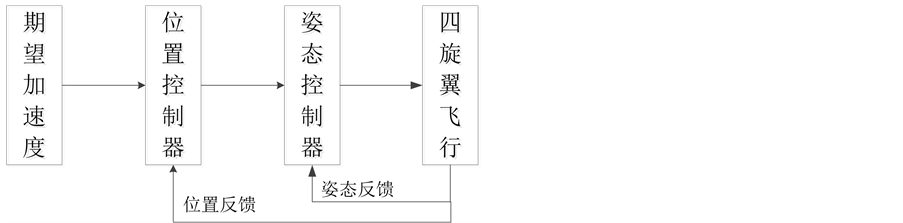
Figure 2. Controller structure diagram
图2. 控制器结构示意图
3.1. 姿态控制
飞行器在飞行过程中需要实时精确控制飞行姿态，通过机身坐标系检测飞行器在
轴上角度和角速度，然后对飞行器姿态采用内环控制，使飞行器到达期望的姿态角。
假设
为期望姿态角，
为机身传感器采集的姿态角数据，如陀螺仪和加速度计联合测量的机身当前的姿态角。两者的偏差
作为内环PID控制器的输入，内环PID控制器输出信号为
。
(1)
式中，
为
轴上比例、积分和微分的控制参数。
3.2. 位置控制
四旋翼飞行器飞行任务由任务规划、路径规划和姿态控制组成。飞行器在空中悬停，当俯仰或横滚获得一个偏航角产生加速度时，飞行器由初始点进行旋进运动匀速飞向目标点。要使飞行器保持匀速飞行，必须进行姿态控制使当前姿态角快速收敛于目标姿态角。
假设目标点坐标为
，飞行器当前的位置坐标
，可通过GPS和气压计计算出(GPS计算出经度和纬度的是地里坐标系，转换到欧拉坐标系为
轴，气压计算出高度为
轴)。飞行器在悬停后以加速度
向目标坐标点飞行，改变1个电机的转速提供合适的升力，其余三个电机的转速保持悬停时转速一致。忽略空气阻力的影响，升力分解为：
(2)
式中，
为升力，
为偏航角。
将公式(2)化简得：
(3)
当自动由起点由稳定加速度飞行目标点时，可以计算出偏航角
(4)
通过偏航角的大小计算出点击需要的转速，以控制它需要的升力。
3.3. 单神经元PID控制器
单神经元PID控制器是将神经网络与传统的PID控制相结合产生一种改进控制方法，具有自适应、自组织功能等特点 [8] ，能较大改善经典非线性动态对象的运动变化，能够适应复杂环境中过程变化的时变特性，保证控制系统在最佳的状态下运行。其控制原理如图3所示。
图3中，状态变换器的输入反映被控对象的控制设定状态。设
为设定值，
为输出值，经过状态变换器转换成神经元的输
分别为
(5)
(6)
(7)
(8)
单神经元PID的控制算法为：
(9)
式中，
为对应
输入的加权系数，
为神经元的比例系数，
的大小决定系统的收敛速度，过大使系统的超调量加大引起不稳定，过小使收敛速度慢，因此
取值适中。
为函数
的阀值。
根据(7)~(10)可知，式(8)具有按偏差的比例、积分和微分的输入值，故
可以作为增量式PID的比例、积分和微分的系数：
(10)
式中，
分别表示比例、积分和微分的学习速率。
4. 实验结果及分析
使用MATLAB的simulink模块根据以上的四旋翼飞行器的运动模型及其控制器，通过双闭环单神经元PID控制器控制四旋翼飞行器飞行，假设飞行器由悬停运动起飞至目标点。起点设为(0, 0, 1)，沿x轴正方向以0.3 m/s匀速速度飞行，通过仿真可得其飞行轨迹曲线和姿态曲线(图4~图6)。
Figure 3. The principle of control of single neuron PID
图3. 单神经元PID的控制原理
5. 总结
本文针对四旋翼无人飞行器数学建模、位置控制和姿态控制进行详细分析，提出将单神经元PID控制器与外环位置控制和内环姿态控制相结合，使飞行器手动整定参数变为自动整定参数，提升系统的鲁棒性，并通过仿真证实此方法可行。