1. 简介
对于黑洞引力场微扰的研究是目前很活跃的一个课题。研究人员相信对黑洞微扰的数值模拟研究将会有助于对现存的引力理论的进一步理解 [1] [2] [3] 。从Regge和Wheeler的开创性工作开始,黑洞时空中微扰场的众多力学性质得到了深入而广泛的研究 [4] [5] [6] 。York最早尝试了将准模与Hawking辐射联系起来 [7] 。尤其是Hod提出了黑洞的一些量子特性与其准模密切相关 [8] 。我们知道,Bekenstein建议黑洞的面积有一系列分立的谱。面积谱的特征值是规则分布的,并且与黑洞的熵相关 [9] 。对于一个质量为M的Schwarzschild黑洞,通过Nollert [10] 以及迟些时候Andersson [11] 等人的数值研究,人们发现准模的实部有如下的关系:
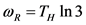 (1)
(1)
这里TH是黑洞的Hawking温度 [12] 。这是一个很让人惊奇的有趣结果。这意味着那些虚部无限大并对引力波信号无突出贡献的模态的确是有一定的物理意义而不能被忽略的。根据这一结论,Dreye甚至修改在圈量子引力中的Barbero-Immirzi参数 [13] 。因为在圈量子引力理论中,仅当 时才能正确的预测出Bekenstein-Hawking熵,从而根据这一点Barbero-Immirzi参数得以确定。
时才能正确的预测出Bekenstein-Hawking熵,从而根据这一点Barbero-Immirzi参数得以确定。
值得指出的是,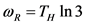 这个关系式的得到,首先是出自于数值计算,稍后这样的完美形式才被发现,随后研究人员通过挖掘它的意义,才又进一步定出了一些相关结论。所以,这个形式的发现是一件非常有意义的事情。
这个关系式的得到,首先是出自于数值计算,稍后这样的完美形式才被发现,随后研究人员通过挖掘它的意义,才又进一步定出了一些相关结论。所以,这个形式的发现是一件非常有意义的事情。
利用Teukolsky方程 [14] [15] [16] ,本文研究了普朗克尺度下的旋转Kerr黑洞,针对其准模分析,我们也发现了一个很有趣的结果。我们的数值计算结果显示普朗克尺度下的Kerr黑洞难以置信的给出了一个实部对应于e/3的准模。这一数值结果,包括相应的物理过程与物理意义可能相当让人惊讶,而我们也尝试着对这一结果进行了分析。
本文第二部分简要介绍了与结果相关的微扰方程以及数值计算方法。我们罗列了Teukolsky方程以及一些相关的数值分析方法。在第三部分中,我们把第二部分的方程应用到了一个极端的情况,即让Kerr黑洞处于面积极小的情况,并使其自旋为2。让人惊奇的是,这里的计算结果可以与最小电荷单元e/3相联系。这一结果来自于普朗克尺度下Kerr黑洞的准模分析。如果这一结果是有意义的,那么我们可能将获得一个最小单位电荷的产生机制。我们并对这一结果进行了分析与说明。第四部分给出了结论。
2. 理论与数值计算方法
旋转Kerr黑洞的时空可以被Boyer-Lindquist坐标系下的如下线元所描述:
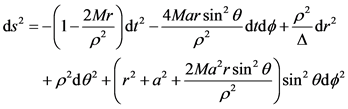 (2)
(2)
这里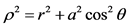 ,
, ,M是质量,a是黑洞单位质量的角动量。(这里我们应用了引力单位制
,M是质量,a是黑洞单位质量的角动量。(这里我们应用了引力单位制 )。
)。
利用著名的Teukolsky主方程,Teukolsky率先研究了旋转相对论物体的微扰问题 [14] [15] [16] 。基于相应的Newman-Penrose标量,Teukolsky描述了不同自旋s = 0, ±1/2, ±1, ±3/2, ±2下的微扰波函数 所遵守的主方程 [17] 。在给Teukolsky主方程设置合适的边界条件后,可以获得Kerr黑洞的准模。大量参考文献给出了主方程数值计算各样重要的结果 [18] [19] [20] [21] 。Teukolsky主方程的一个重要特性是,在Boyer-Lindquist坐标系下,
所遵守的主方程 [17] 。在给Teukolsky主方程设置合适的边界条件后,可以获得Kerr黑洞的准模。大量参考文献给出了主方程数值计算各样重要的结果 [18] [19] [20] [21] 。Teukolsky主方程的一个重要特性是,在Boyer-Lindquist坐标系下,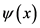 可以坐标分解为
可以坐标分解为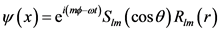 ,而这会使得计算大为简化。
,而这会使得计算大为简化。
Detweiler率先给出了Kerr准模的数值计算结果 [22] [23] 。在Kerr黑洞情况下,由于非球对称,微扰问题不能象Schwarzchild黑洞那样归为径向的一个普通的微分方程。它将会成为两个耦合在一起的微分方程,其中一个是径向的微扰方程,另一个是关于角向部分的微扰方程。因此,我们不得不同时解两个微分方程。这样做相对比较困难。不过通过领域内研究人员的大量工作,求解方程可以通过下面的方式来进行 [24] [25] [26] [27] 。假设:
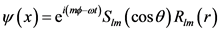 (3)
(3)
这里 是Boyer-Lindquist坐标。代入Teukolsky主方程,马上可以给出了一个径向方程和一个角向方程,它们通过分离变量
是Boyer-Lindquist坐标。代入Teukolsky主方程,马上可以给出了一个径向方程和一个角向方程,它们通过分离变量 耦合在一起。这里
耦合在一起。这里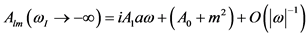
径向的微分方程可以约化为 [25] :
 (4)
(4)
这里
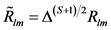 (5)
(5)
且:
 (6)
(6)
 (7)
(7)
 (8)
(8)
自旋权重参数s的取值给出了不同场的方程,如引力场(s = 2),电磁场(s = 1),标量场(s = 0),以及二分量的中微子场(s = 1/2)。
方程(4)给出了一个分析解,Kerr黑洞准模的实部可以被写为 ,其中
,其中 ,且:
,且:
 (9)
(9)
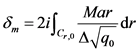 (10)
(10)
这些积分的数值计算一般需要花费很长时间,而文献25给出了一个相当简化的椭圆函数表达式形式 [25] 。
3. 数值计算结果
采用与参考文献 [24] [25] [26] [27] 类似的方法,我们进行了数值计算 [24] [25] [26] [27] 。在图1中,横坐标是单位质量角动量对质量的比值,纵坐标是准模频率实部乘上质量。图中曲线与参考文献 [24] [25]
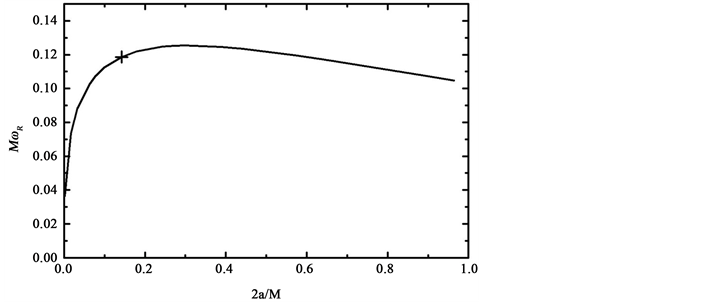
Figure 1. The horizontal axis is for the angular momentum to mass ratio, and the vertical axis is for the real part of the quasi normal mode frequency multiplied by mass versus. The cross point has the minimum surface area and J = 2. Here we chose m = −2, rather than m = −1, as compared with that in reference [24] and [25]
图1. 横坐标是单位质量角动量对质量的比值,纵坐标是准模频率实部乘上质量。标十字的点有最小面积且自旋角动量为J = 2。和文献 [24] 与 [25] 不同的是,这里我们选择了m = −2, 而不是 m = −1
[26] [27] 中的数值计算结果符合的很好,只是我们在图中选择了m = −2,而不是m = −1 [28] [29] 。
因为我们关心的是在被推到极限情况下Kerr黑洞的准模,所以我们特别考虑了图中曲线上标为十字形的那一点。对于这一点,它对应的面积为4ln3,并且角动量为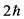 。因此,Kerr黑洞总的质量可表示如下:
。因此,Kerr黑洞总的质量可表示如下:
 (11)
(11)
因为微扰值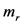 与Kerr黑洞的质量相比是个小量,且Kerr黑洞的尺度要比普朗克尺度大,所以这里面积和角动量被量子化了,而引力势未做量子化 [30] 。
与Kerr黑洞的质量相比是个小量,且Kerr黑洞的尺度要比普朗克尺度大,所以这里面积和角动量被量子化了,而引力势未做量子化 [30] 。
角动量与质量的比值为:
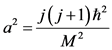 (12)
(12)
根据等式(11),我们可以得到黑洞的最小质量是4.1527普朗克质量。对图1中由十字形所表示的点,可得到准模实部对应的能量为5.5901e + 7 J,而这相应于 。而十分让人惊讶的是,利用等式
。而十分让人惊讶的是,利用等式 ,这最终给出了
,这最终给出了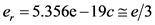 ,这里e是电荷单位。
,这里e是电荷单位。
等式 的来源可能需要更进一步的解释。简而言之,该等式来至于等式
的来源可能需要更进一步的解释。简而言之,该等式来至于等式 。我们知道,让两个
。我们知道,让两个 放置相距r,则它们之间的相互作用力为
放置相距r,则它们之间的相互作用力为 。而让两个
。而让两个 放置相距r,它们之间的作用力为
放置相距r,它们之间的作用力为 。让等式
。让等式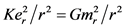 成立,即认为两个
成立,即认为两个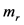 之间的引力即是等效于两个
之间的引力即是等效于两个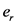 之间的静电力,这给出了当质量为
之间的静电力,这给出了当质量为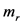 时,所对应的 值大小。经计算,恰好为
时,所对应的 值大小。经计算,恰好为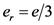 。
。
此外,我们知道对两个电荷,如果两个电荷不同号,则相互吸引,而如果两个电荷同号,则相互排斥。这一点是与引力不同的。为说明这个规律与我们结果并不相背,下面我们花一定的篇幅来做解释。
我们先比较了准模的能量与根据Penrose过程从黑洞的能层所能提取出来的能量。根据Penrose过程,不可约化质量可写为:
 (13)
(13)
所以能被提取出来的质量为:
 (14)
(14)
根据公式(11)-(14),由Pensrose过程,不可约化质量是2.2939e−10 kg,大大小于e/3所对应的准模能量。由于从这个最小Kerr黑洞所能提取出的最大能量小于e/3所对应的准模的能量,因此对于这个最小黑洞,当黑洞受到微扰,并不能从黑洞提取能量。它只能吸收能量或什么都不做。这意味着对于m = 0, +2, −2的标量场微扰,我们只能有m = 0, +2。因而微扰得到的 只能取负号。
只能取负号。
我们知道,负质量的物体具有如下规律,即是两个负质量物体之间的作用力会使得它们相互排斥。如果认为电荷具有质量的起源,则这一点可以用于解释两个负电荷之间存在的力是排斥力的情况。(关于负质量的物理特性可以特别关注最近的报导 [31] [32] )进一步对于Kerr黑洞为负质量的情况,则可以得到从中提取出来的质量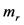 具有正号。这可以解释两个正号的电荷之间依然是排斥力。两个正质量的
具有正号。这可以解释两个正号的电荷之间依然是排斥力。两个正质量的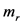 将会在
将会在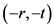 时空相互排斥,因为在转换到
时空相互排斥,因为在转换到 时空后,根据CPT对称性原理,两个负号的
时空后,根据CPT对称性原理,两个负号的 之间将会相互排斥。根据上面的阐述,也可以很自然的解释两个不同电荷之间的作用力是吸引力。另外,上述解释也说明了静电力与引力有相同类似的起源,事实上它们都遵守平方反比定律。
之间将会相互排斥。根据上面的阐述,也可以很自然的解释两个不同电荷之间的作用力是吸引力。另外,上述解释也说明了静电力与引力有相同类似的起源,事实上它们都遵守平方反比定律。
需要进一步对图1进行解释的是,当面积固定为最小值时,在十字符号左面的曲线可以通过角动量对面积的比值得到。当自旋值固定为2时,十字符号右面的曲线可通过增加面积得到。增加角动量到大于自旋值2看起来并没有太大的物理意义,因为一般不会考虑自旋值大于2的情况。而十字符号右面可能具有的物理图像是让一些最小的Schwarzchild黑洞凝聚在一起,且凝聚后具有自旋2。这一种情况可能需要进一步的考虑,包括这些具有最小面积的Schwarzchild黑洞是如何凝聚起来的以及如何相互作用的。但因为这是一个凝聚的态,而不是最小面积的情况,这里我们不准备对它再进一步的考虑。本文主要阐述的是当微扰最小的Kerr黑洞时,可以得到最小的电荷单位是e/3。而且我们建立了相应的模型,并作了一些解释来说明这个结论。
最后,需要指出的是,除去上述的看起来自洽的理论解释,包括建模推理等等,我们并未能提出任何实验方法去证实这些看起来非常大胆的理论。因此,可能有人甚至认为上面的结果不具有真实性。不过,我们最重要的结果是得到了单位电荷的值是e/3,并可以使误差达到小数点后的第三位。这是一级近似所得到的结果,如果进一步的在二级近似的情况下,可以进一步的提升误差率到小数点后更多的位数,则将会大大的支持本文的结论。但是,这可能将是很繁重的一项工作。
4. 结论
本文给出了一个相当让人惊奇的结果,即微扰最小的普朗克尺度下的Kerr黑洞可以得到最小的单位电荷e/3。我们试着自恰的解释了这一结果。特别是事实上给出了引力与静电力基本同源的结论,即由e/3所代表的静电力与由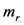 所代表的引力计算的受力结果等效。需要指出的是,目前并没有提出可以实验验证这一结论的方法。但是如果二级近似能够进一步的提升所得结果的精确性,则会给本文提供更大的支持。
所代表的引力计算的受力结果等效。需要指出的是,目前并没有提出可以实验验证这一结论的方法。但是如果二级近似能够进一步的提升所得结果的精确性,则会给本文提供更大的支持。