基于FQ_n和圈的细胞分裂生长网络FQCC(n,k)及其性质

Based on FQ_n and Cycles Cell-Breeding Network FQCC(n,k) and Its Properties

摘要: 折叠立方体连通圈网络FQCC(n) (n > 1)是一类典型的互连网络，它是3正则的。师海忠根据折叠立方体连通圈网络i>FQCC(n) (n > 1)和细胞分裂生长图模型设计出了一种新的互连网络——FQCC(n,k) (n > 1，k是非负整数)：用三长的圈代替FQCC(n)的每个顶点且圈中每个顶点恰位于折叠立方体连通圈网络FQCC(n) (n > 1)中与该顶点关联的一条边上，得到新的网络FQCC(n,1)；再类似的用三长的圈代替FQCC(n,1)的每个顶点得FQCC(n,2)，循环执行上述方法k次得到的新网络称为FQCC(n,k) (n > 1，k是非负整数)。该网络FQCC(n,k)在保持了FQCC(n)的小的固定的度(为3)的特性外，还有比FQCC(n)更好的扩展性。进而提出了猜想：FQCC(n,k)是Hamilton图。赵媛证明了FQCC(2,k)是平面图和Hamilton图，还证明了FQCC(n,k) (k > 1)不是点可迁的。

Abstract: The folded cube-connected cycles network FQCC(n) (n > 1) is a classic interconnection network; it is 3 regular. On the basis of the folded cube-connected cycles network FQCC(n) (n > 1) and cell- breeding graph model for interconnection network, FQCC(n,k) (n > 1, k is not a negative integer) is designed by Haizhong Shi: each vertex in the folded cube-connected cycles network FQCC(n) (n > 1) is replaced by the cycles of length 3, and the vertex in every cycle is located on the edge of the folded cube-connected cycles connected to the vertex, then we called the new network FQCC(n,1); in similar way each vertex in the folded cube-connected cycles network FQCC(n,1) (n > 1) is replaced by the cycles of length 3, then we called the new network FQCC(n,2), looping execution the above method k times, and then get the new network—FQCC(n,k) (n > 1, k is not a negative integer). The network FQCC(n,k) keeps small or fixed degree (is 3) of FQCC(n), and has better extendability than FQCC(n). Furthermore proposed a conjecture: FQCC(n,k) is Hamiltonian. Yuan Zhao proofs that FQCC(2,k) is planar and Hamiltonian, and that FQCC(n,k) (k > 1) is not vertex- transitive.

1. 引言

互连网络是超级计算机的重要组成部分。网络遵循八个原则：小的固定顶点度；小通信传输延迟；简单的路由算法；均匀性或对称性；高容错性；可扩性；可嵌入性；有效的布图算法。大规模集成电路技术的出现和现代通信技术的飞速发展要求人们设计出多核的互连网络，对这种网络来讲网络的平面性是一项很重要的指标。互连网络的基本拓扑结构是连通图G(V,E)。其中V是处理器的集合，E是网络通信链路的集合 [1] [2] 。

许多学者设计出了多种互连网络，例如：折叠Petersen立方体、折叠立方体、正则图连通圈网络(折叠立方体连通圈网络，立方体连通圈网络等)、细胞分裂生长图模型、层次环群论模型等并给出了它们的部分性质 [3] - [17] 。这些互连网络都有许多优点，也各自存在一些缺点。比如折叠立方体，它的度(n + 1)随着规模( $2^n$ )的增大而增大。折叠立方体连通圈具有优点——小的固定的度(都为3)，但它的扩展性较差。在这篇文章中，根据文献 [8] 和 [10] 中提出的设计互连网络的新思想，师海忠设计出了新的互连网络 $FQCC\left(n,k\right)\left(n\ge 2,k\ge 0\right)$ 。除了保持折叠立方体连通圈 $FQCC\left(n\right)$ 的优点——小的固定的度(为3)外，当固定 $n$ 之后，它有较好的可扩展性，即规模可随着 $k$ 的增大而增大。特别是赵媛证明了 $FQCC\left(2,k\right)$ 是个平面图和Hamilton图，还证明了 $FQCC\left(n,k\right)\left(k\ge 2\right)$ 不是点可迁的。

本文其余结构是：第2节，基本概念；第3节，新互连网络 $k$ 及其性质；第4节，结束语。

2. 基本概念

定义1 [14] ：令 $x=x_0{x}_1\cdots x_{n-1}$ 是一个n比特二元串，我们用 ${\left(x\right)}_j$ 来定义比特 $x_j$ 。令 $x={\left(y\right)}^i$ 当 $x$ 和 $y$ 仅在第 $i$ 个位置比特不同。

定义2：如果两个顶点 $x=x_0{x}_1\cdots x_{n-1}$ 和 $y=y_0{y}_1\cdots y_{n-1}$ 有 $y_i=1-x_i\left(i=0,1,\cdots ,n-1\right)$ ，那么我们就记做 $y=\bar{x}$ 。我们说 $x$ 和 $\bar{x}$ 是互补的。

定义3：n维折叠立方体连通圈 $FQCC\left(n\right)$ 定义为一个无向图，它有 $\left(n+1\right)\cdot 2^n$ 个顶点，记做 $\left(x,l\right)$ ，其中 $x=x_0{x}_1\cdots x_{n-1}$ 是一个n比特二元串， $l$ 是0到n的一个正整数，两个顶点 $\left(x,l\right)$ ， $\left(y,l^{\prime }\right)$ 相连当且仅当(i) $x=y$ 且 $\left|l-l^{\prime }\right|=1$ 或者(ii) $0\le l=l^{\prime }\le n-1$ 且 $y={\left(x\right)}^l$ 或者(iii) $l=l^{\prime }=n$ 且 $y=\bar{x}$ 。

定义4：我们给出新网络 $FQCC\left(2,k\right)\left(k\ge 0\right)$ 的严格数学定义， $FQCC\left(2,k\right)$ 的顶点记作 $\left(x,l\left(k+1\right)\right)$ ，其中 $x$ 是2比特二元串， $l\left(k+1\right)=l_1{l}_2\cdots l_{k+1}$ ， $l_i$ 是0到2的整数。两个顶点 $\left(x,l\left(k+1\right)\right)$ 和 $\left(y,l^{\prime }\left(k+1\right)\right)$ 相连当且仅当(i) $y={\left(x\right)}^j\left(j=0,1\right)$ 且 $l_i={l^{\prime }}_i=j\left(1\le i\le k+1\right)$ ；或者(ii) $y=\bar{x}$ 且 $l_i={l^{\prime }}_i=2\left(1\le i\le k+1\right)$ ；或者(iii) $x=y$ 且 $l_k\ne {l^{\prime }}_k$ ， $l_k\ne l_{k+1}$ ， ${l^{\prime }}_k\ne {l^{\prime }}_{k+1}$ ， $l_i={l^{\prime }}_i\left(i\ne k\right)$ ；或者(iv) $x=y$ 且 $\left(x,l\left(k\right)\right)$ ， $\left(y,l^{\prime }\left(k\right)\right)\in V\left(FQCC\left(2,k-1\right)\right)$ 且 $\left(\left(x,l\left(k\right)\right),\left(y,l^{\prime }\left(k\right)\right)\right)\in E\left(FQCC\left(2,k-1\right)\right)$ 且 $l_k=l_{k+1}={l^{\prime }}_{k+1}={l^{\prime }}_k$ ；或者(v) $x=y$ 且 $l_{k+1}\ne {l^{\prime }}_{k+1}$ ， $l_i={l^{\prime }}_i\left(1\le i\le k\right)$ 。如图2、图3。

定义5 [2] ：若一个图具有这样的一个图形，它的边仅在端点处相交，则该图称为平面图。

定义6：G的Hamilton圈是指包含G的每个顶点的圈。

定义7：一个图若包含Hamilton圈，则称这个图是Hamilton图。

定义8 [15] ：若一个图中任意两个顶点之间都有一条Hamilton路，则称这个图为Hamilton连通图。

定义9 [1] ：如果G是点可迁的，那么对G的每对顶点 $x$ 和 $y$ ，存在 $\theta \in Aut\left(G\right)$ ，使得 $y=\theta \left(x\right)$ 。

3. 新互连网络FQCC(n,k)及其性质

3.1. FQCC(n,k)及其基本性质

在这一节中师海忠设计出了新互连网络 $FQCC\left(n,k\right)$ ：用三长的圈代替 $FQCC\left(n\right)$ 的每个顶点且圈中每个顶点恰位于折叠立方体连通圈网络 $FQCC\left(n\right)\left(n\ge 2\right)$ 中与该顶点关联的一条边上，得到新的网络 $FQCC\left(n,1\right)$ ；再类似的用三长的圈代替 $FQCC\left(n,1\right)$ 的每个顶点得 $FQCC\left(n,2\right)$ ，循环执行上述方法 $k$ 次得到的新网络称为 $FQCC\left(n,k\right)\left(n\ge 2,k\ge 0\right)$ ，注意 $FQCC\left(n,0\right)$ 即为 $FQCC\left(n\right)$ 。新互连网络 $FQCC\left(n,k\right)\left(n\ge 2,k\ge 0\right)$ 有 $\left(n+1\right)2^n{3}^k$ 个顶点， $\left(n+1\right)2^{n-1}{3}^{k+1}$ 条边，且它的度为3。 $FQCC\left(n,k\right)$ 比 $FQCC\left(n\right)$ 有更好的扩展性，即当固定 $n$ 之后，规模( $\left(n+1\right)2^n{3}^k$ )随着 $k$ 的增大而增大。特别是 $FQCC\left(2,k\right)$ 有较好的性质(见3.2节)。

3.2. FQCC(2,k)及其性质

在这一节中，赵媛讨论了 $FQCC\left(2,k\right)$ 的平面性、Hamilton性、点可迁性。

定理1： $FQCC\left(2,k\right)\left(k\ge 0\right)$ 是平面图。

证明：显然 $F{Q}_2$ 是平面图，如图1。所以 $FQCC\left(2\right)$ 即 $FQCC\left(2,0\right)$ 是平面图，如图2。那么 $FQCC\left(2,k\right)$ 也是平面图，如图3。

定理2： $FQCC\left(2,k\right)$ 是Hamilton图。

证明：当 $k=0$ 时，我们可以在 $FQCC\left(2,0\right)$ (也就是 $FQCC\left(2\right)$ )中找到一个Hamilton圈：(00,0)-(00,2) -(11,2)-(11,0)-(11,1)-(10,1)-(10,0)-(10,2)-(01,2)-(01,0)-(01,1)-(00,1)-(00,0)。显然 $FQCC\left(2\right)$ 是Hamilton图。

当 $k=1$ 时， $FQCC\left(2,0\right)$ 中的顶点 $\left(x,l_1\right)$ 变成了 $\left(x,l_1{l}_1\right)$ 。我们可以找到路P₁<(00,00),(00,01),(00,21), (00,20),(00,22)>来代替边((00,0),(00,2))；路P₂<(00,22),(11,22)>来代替边((00,2),(11,2))；路P₃<(11,22),(11,20), (11,21),(11,01),(11,00)>来代替边((11,2),(11,0))；路P4<(11,00),(11,02),(11,12),(11,10), (11,11)>来代替边((11,0),(11,1))；路P₅<(11,11),(10,11)>来代替边((11,1),(10,1))；路P6<(10,11),(10,10), (10,12),(10,02),(10,00)>

Figure 1. Planar graph FQ₂

图1. 平面图FQ₂

Figure 2. Planar graph $FQCC\left(2,0\right)$

图2. 平面图 $FQCC\left(2,0\right)$

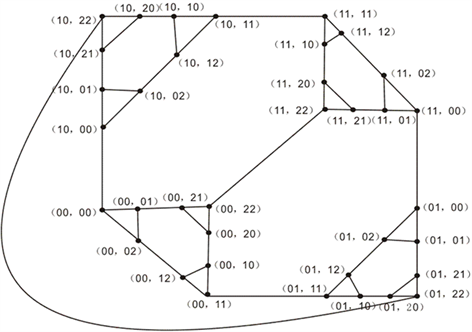
Figure 3. Planar graph $FQCC\left(2,1\right)$

图3. 平面图 $FQCC\left(2,1\right)$

来代替边((10,1),(10,0))；路P₇<(10,00),(10,01),(10,21),(10,2),(10,22)>来代替边((10,0),(10,2))；路P₈<(10,22), (01,22)>来代替边((10,2),(01,2))；路P₉<(01,22),(01,20),(01,21),(01,01),(01,00)>来代替边((01,2),(01,0))；路P₁₀<(01,00),(01,02),(01,12),(01,10),(01,11)>来代替边((01,0),(01,1))；路P₁₁<(01,11),(00,11)>来代替边((01,1),(00,1))；路P₁₂<(00,11),(00,10),(00,12),(00, 02),(00,00)>来代替边((00,1),(00,0))。令 $C={\displaystyle \underset{i=1}{\overset{12}{\cup }}{P}_i}$ ，则 $C$ 是一个Hamilton圈，所以 $FQCC\left(2,1\right)$ 是Hamilton图。并且路 $P_2$ ， $P_5$ ， $P_8$ ， $P_{11}$ 的长为1，其余路的长为4。

以此类推，当 $k=n\left(n\ge 2\right)$ 时， $FQCC\left(2,0\right)$ 中的顶点 $\left(x,l_1\right)$ 变为 $\left(x,l\left(k+1\right)\right)$ 。其中 $l=l_1{l}_2\cdots l_{n+1}$ ， $l_1=l_2=\cdots =l_{n+1}$ 。我们可以找到路 $P_i\langle \left(\left(x,l\right),p_i,\left(y,l^{\prime }\right)\right)\rangle \left(1\le i\le 12\right)$ 来代替边 $\left(\left(x,l_1\right),\left(y,{l^{\prime }}_1\right)\right)$ 。令 $C={\displaystyle \underset{i=1}{\overset{12}{\cup }}{P}_i}$ ，则 $C$ 是 $FQCC\left(2,k\right)$ 的一个Hamilton圈，所以 $FQCC\left(2,k\right)$ 是Hamilton图。其中路 $P_2$ ， $P_5$ ， $P_8$ ， $P_{11}$ 的长为1，其余路的长为 $0.5\left(3^{k+1}-1\right)$ 。

由此，师海忠提出如下猜想：

猜想3： $FQCC\left(n,k\right)$ 是Hamilton图。

定理4： $FQCC\left(2,0\right)$ 是Hamilton连通图。

证明：由定义8可知，顶点(00,0)和(00,1)之间有一条Hamilton路

P₁：(00,0)-(00,2)-(11,2)-(11,0)-(11,1)-(10,1)-(10,0)-(10,2)-(01,2)-(01,0)-(01,1)-(00,1)。以此类推，

P₂{(00,0),(00,2)}:(00,0)-(00,1)-(01,1)-(01,0)-(01,2)-(10,2)-(10,0)-(10,1)-(11,1)-(11,0)-(11,2)-(00,2).

P₃{(00,0),(01,0)}:(00,0)-(00,1)-(00,2)-(11,2)-(11,0)-(11,1)-(10,1)-(10,0)-(10,2)-(01,2)-(01,1)-(01,0).

P₄{(00,0),(01,1)}:(00,0)-(00,1)-(00,2)-(11,2)-(11,0)-(11,1)-(10,1)-(10,0)-(10,2)-(01,2)-(01,0)-(01,1).

P₅{(00,0),(01,2)}:(00,0)-(10,0)-(10,2)-(10,1)-(11,1)-(11,0)-(11,2)-(00,2)-(00,1)-(01,1)-(01,0)-(01,2).

P₆{(00,0),(10,0)}:(00,0)-(00,1)-(00,2)-(11,2)-(11,1)-(11,0)-(01,0)-(01,1)-(01,2)-(10,2)-(10,1)-(10,0).

P₇{(00,0),(10,1)}:(00,0)-(00,1)-(00,2)-(11,2)-(11,1)-(11,0)-(01,0)-(01,1)-(01,2)-(10,2)-(10,0)-(10,1).

P₈{(00,0),(10,2)}:(00,0)-(00,2)-(00,1)-(01,1)-(01,2)-(01,0)-(11,0)-(11,2)-(11,1)-(10,1)-(10,0)-(10,2).

P₉{(00,0),(11,0)}:(00,0)-(00,2)-(00,1)-(01,1)-(01,0)-(01,2)-(10,2)-(10,0)-(10,1)-(11,1)-(11,2)-(11,0).

P₁₀{(00,0),(11,1)}:(00,0)-(00,1)-(00,2)-(11,2)-(11,0)-(01,0)-(01,1)-(01,2)-(10,2)-(10,0)-(10,1)-(11,1).

P₁₁{(00,0),(11,2)}:(00,0)-(00,2)-(00,1)-(01,1)-(01,0)-(01,2)-(10,2)-(10,0)-(10,1)-(11,1)-(11,0)-(11,2).

P₁₂{(00,1),(00,2)}:(00,1)-(00,0)-(10,0)-(10,1)-(10,2)-(01,2)-(01,1)-(01,0)-(11,0)-(11,1)-(11,2)-(00,2).

P₁₃{(00,1),(01,0)}:(00,1)-(00,0)-(00,2)-(11,2)-(11,0)-(11,1)-(10,1)-(10,0)-(10,2)-(01,2)-(01,1)-(01,0).

P₁₄{(00,1),(01,1)}:(00,1)-(00,2)-(00,0)-(10,0)-(10,2)-(10,1)-(11,1)-(11,2)-(11,0)-(01,0)-(01,2)-(01,1).

P₁₅{(00,1),(01,2)}:(00,1)-(00,2)-(00,0)-(10,0)-(10,2)-(10,1)-(11,1)-(11,2)-(11,0)-(01,0)-(01,1)-(01,2).

P₁₆{(00,1),(10,0)}:(00,1)-(00,0)-(00,2)-(11,2)-(11,1)-(11,0)-(01,0)-(01,1)-(01,2)-(10,2)-(10,1)-(10,0).

P₁₇{(00,1),(10,1)}:(00,1)-(00,0)-(00,2)-(11,2)-(11,1)-(11,0)-(01,0)-(01,1)-(01,2)-(10,2)-(10,0)-(10,1).

P₁₈{(00,1),(10,2)}:(00,1)-(00,2)-(00,0)-(10,0)-(10,1)-(11,1)-(11,2)-(11,0)-(01,0)-(01,1)-(01,2)-(10,2).

P₁₉{(00,1),(11,0)}:(00,1)-(00,0)-(00,2)-(11,2)-(11,1)-(10,1)-(10,0)-(10,2)-(01,2)-(01,1)-(01,0)-(11,0).

P₂₀{(00,1),(11,1)}:(00,1)-(00,2)-(00,0)-(10,0)-(10,1)-(10,2)-(01,2)-(01,1)-(01,0)-(11,0)-(11,2)-(11,1).

P₂₁{(00,1),(11,2)}:(00,1)-(00,2)-(00,0)-(10,0)-(10,1)-(10,2)-(01,2)-(01,1)-(01,0)-(11,0)-(11,1)-(11,2).

P₂₂{(00,2),(01,0)}:(00,2)-(00,0)-(00,1)-(01,1)-(01,2)-(10,2)-(10,0)-(10,1)-(11,1)-(11,2)-(11,0)-(01,0).

P₂₃{(00,2),(01,1)}:(00,2)-(00,1)-(00,0)-(10,0)-(10,2)-(10,1)-(11,1)-(11,2)-(11,0)-(01,0)-(01,2)-(01,1).

P₂₄{(00,2),(01,2)}:(00,2)-(00,1)-(00,0)-(10,0)-(10,2)-(10,1)-(11,1)-(11,2)-(11,0)-(01,0)-(01,1)-(01,2).

P₂₅{(00,2),(10,0)}:(00,2)-(00,0)-(00,1)-(01,1)-(01,2)-(01,0)-(11,0)-(11,2)-(11,1)-(10,1)-(10,2)-(10,0).

P₂₆{(00,0),(10,1)}:(00,2)-(00,1)-(00,0)-(10,0)-(10,2)-(01,2)-(01,1)-(01,0)-(11,0)-(11,2)-(11,1)-(10,1).

P₂₇{(00,2),(10,2)}:(00,2)-(00,0)-(00,1)-(01,1)-(01,2)-(01,0)-(11,0)-(11,2)-(11,1)-(10,1)-(10,0)-(10,2).

P₂₈{(00,2),(11,0)}:(00,2)-(00,0)-(00,1)-(01,1)-(01,0)-(01,2)-(10,2)-(10,0)-(10,1)-(11,1)-(11,2)-(11,0).

P₂₉{(00,2),(11,1)}:(00,2)-(00,1)-(00,0)-(10,0)-(10,1)-(10,2)-(01,2)-(01,1)-(01,0)-(11,0)-(11,2)-(11,1).

P₃₀{(00,2),(11,2)}:(00,2)-(00,0)-(00,1)-(01,1)-(01,0)-(01,2)-(10,2)-(10,0)-(10,1)-(11,1)-(11,0)-(11,2).

P₃₁{(01,0),(01,1)}:(01,0)-(01,2)-(10,2)-(10,0)-(10,1)-(11,1)-(11,0)-(11,2)-(00,2)-(00,0)-(00,1)-(01,1).

P₃₂{(01,0),(01,2)}:(01,0)-(01,1)-(00,1)-(00,0)-(00,2)-(11,2)-(11,0)-(11,1)-(10,1)-(10,0)-(10,2)-(01,2).

P₃₃{(01,0),(10,0)}:(01,0)-(01,2)-(01,1)-(00,1)-(00,0)-(00,2)-(11,2)-(11,0)-(11,1)-(10,1)-(10,2)-(10,0).

P₃₄{(01,0),(10,1)}:(01,0)-(01,1)-(01,2)-(10,2)-(10,0)-(00,0)-(00,1)-(00,2)-(11,2)-(11,0)-(11,1)-(10,1).

P₃₅{(01,0),(10,2)}:(01,0)-(01,2)-(01,1)-(00,1)-(00,0)-(00,2)-(11,2)-(11,0)-(11,1)-(10,1)-(10,0)-(10,2).

P₃₆{(01,0),(11,0)}:(01,0)-(01,2)-(01,1)-(00,1)-(00,2)-(00,0)-(10,0)-(10,2)-(10,1)-(11,1)-(11,2)-(11,0).

P₃₇{(00,0),(11,1)}:(01,0)-(01,1)-(01,2)-(10,2)-(10,1)-(10,0)-(00,0)-(00,1)-(00,2)-(11,2)-(11,0)-(11,1).

P₃₈{(01,0),(11,2)}:(01,0)-(01,2)-(01,1)-(00,1)-(00,2)-(00,0)-(10,0)-(10,2)-(10,1)-(11,1)-(11,0)-(11,2).

P₃₉{(01,1),(01,2)}:(01,1)-(01,0)-(11,0)-(11,1)-(11,2)-(00,2)-(00,1)-(00,0)-(10,0)-(10,1)-(10,2)-(01,2).

P₄₀{(01,1),(10,0)}:(01,1)-(01,0)-(01,2)-(10,2)-(10,1)-(11,1)-(11,0)-(11,2)-(00,2)-(00,1)-(00,0)-(10,0).

P₄₁{(01,1),(10,1)}:(01,1)-(01,0)-(01,2)-(10,2)-(10,0)-(00,0)-(00,1)-(00,2)-(11,2)-(11,0)-(11,1)-(10,1).

P₄₂{(01,1),(10,2)}:(01,1)-(01,2)-(01,0)-(11,0)-(11,1)-(11,2)-(00,2)-(00,1)-(00,0)-(10,0)-(10,1)-(10,2).

P₄₃{(01,1),(11,0)}:(01,1)-(01,0)-(01,2)-(10,2)-(10,1)-(10,0)-(00,0)-(00,1)-(00,2)-(11,2)-(11,1)-(11,0).

P₄₄{(01,1),(11,1)}:(01,1)-(01,0)-(01,2)-(10,2)-(10,1)-(10,0)-(00,0)-(00,1)-(00,2)-(11,2)-(11,0)-(11,1).

P₄₅{(01,1),(11,2)}:(01,1)-(01,2)-(01,0)-(11,0)-(11,1)-(10,1)-(10,2)-(10,0)-(00,0)-(00,1)-(00,2)-(11,2).

P₄₆{(01,2),(10,0)}:(01,2)-(01,0)-(01,1)-(00,1)-(00,0)-(00,2)-(11,2)-(11,0)-(11,1)-(10,1)-(10,2)-(10,0).

P₄₇{(01,2),(10,1)}:(01,2)-(01,1)-(01,0)-(11,0)-(11,1)-(11,2)-(00,2)-(00,1)-(00,0)-(10,0)-(10,2)-(10,1).

P₄₈{(01,2),(10,2)}:(01,2)-(01,0)-(01,1)-(00,1)-(00,0)-(00,2)-(11,2)-(11,0)-(11,1)-(10,1)-(10,0)-(10,2).

P₄₉{(01,2),(11,0)}:(01,2)-(01,0)-(01,1)-(00,1)-(00,2)-(00,0)-(10,0)-(10,2)-(10,1)-(11,1)-(11,2)-(11,0).

P₅₀{(01,2),(11,1)}:(01,2)-(01,1)-(01,0)-(11,0)-(11,2)-(00,2)-(00,1)-(00,0)-(10,0)-(10,2)-(10,1)-(11,1).

P₅₁{(01,2),(11,2)}:(01,2)-(01,1)-(01,0)-(11,0)-(11,1)-(10,1)-(10,2)-(10,0)-(00,0)-(00,1)-(00,2)-(11,2).

P₅₂{(10,0),(10,1)}:(10,0)-(10,2)-(01,2)-(01,0)-(01,1)-(00,1)-(00,0)-(00,2)-(11,2)-(11,0)-(11,1)-(10,1).

P₅₃{(10,0),(10,2)}:(10,0)-(10,1)-(11,1)-(11,0)-(11,2)-(00,2)-(00,0)-(00,1)-(01,1)-(01,0)-(01,2)-(10,2).

P₅₄{(10,0),(11,0)}:(10,0)-(10,1)-(10,2)-(01,2)-(01,0)-(01,1)-(00,1)-(00,0)-(00,2)-(11,2)-(11,1)-(11,0).

P₅₅{(10,0),(11,1)}:(10,0)-(10,1)-(10,2)-(01,2)-(01,0)-(01,1)-(00,1)-(00,0)-(00,2)-(11,2)-(11,0)-(11,1).

P₅₆{(10,0),(11,2)}:(10,0)-(10,2)-(10,1)-(11,1)-(11,0)-(01,0)-(01,2)-(01,1)-(00,1)-(00,0)-(00,2)-(11,2).

P₅₇{(10,1),(10,2)}:(10,1)-(10,0)-(00,0)-(00,1)-(00,2)-(11,2)-(11,1)-(11,0)-(01,0)-(01,1)-(01,2)-(10,2).

P₅₈{(10,1),(11,0)}:(10,1)-(10,0)-(10,2)-(01,2)-(01,0)-(01,1)-(00,1)-(00,0)-(00,2)-(11,2)-(11,1)-(11,0).

P₅₉{(10,1),(11,1)}:(10,1)-(10,0)-(10,2)-(01,2)-(01,0)-(01,1)-(00,1)-(00,0)-(00,2)-(11,2)-(11,0)-(11,1).

P₆₀{(10,1),(11,2)}:(10,1)-(10,2)-(10,0)-(00,0)-(00,2)-(00,1)-(01,1)-(01,2)-(01,0)-(11,0)-(11,1)-(11,2).

P₆₁{(10,2),(11,0)}:(10,2)-(10,0)-(10,1)-(11,1)-(11,2)-(00,2)-(00,0)-(00,1)-(01,1)-(01,2)-(01,0)-(11,0).

P₆₂{(10,2),(11,1)}:(10,2)-(10,1)-(10,0)-(00,0)-(00,2)-(00,1)-(01,1)-(01,2)-(01,0)-(11,0)-(11,2)-(11,1).

P₆₃{(10,2),(11,2)}:(10,2)-(10,1)-(10,0)-(00,0)-(00,2)-(00,1)-(01,1)-(01,2)-(01,0)-(11,0)-(11,1)-(11,2).

P₆₄{(11,0),(11,1)}:(11,0)-(11,2)-(00,2)-(00,0)-(00,1)-(01,1)-(01,0)-(01,2)-(10,2)-(10,0)-(10,1)-(11,1).

P₆₅{(11,0),(11,2)}:(11,0)-(11,1)-(10,1)-(10,0)-(10,2)-(01,2)-(01,0)-(01,1)-(00,1)-(00,0)-(00,2)-(11,2).

P₆₆{(11,1),(11,2)}:(11,1)-(11,0)-(01,0)-(01,1)-(01,2)-(10,2)-(10,1)-(10,0)-(00,0)-(00,1)-(00,2)-(11,2).

引理5 [1] ：令G是n阶点可迁图，则G的所有n-1阶子图都同构。

定理6： $FQCC\left(2,1\right)$ 不是点可迁的。

证明：为了方便书写，我们将图4中的各顶点简记为1~36。不失一般性，我们在图4中删去顶点1 (记为 $G_b$ ，如图5)，在图4中删去顶点2 (记为 $G_c$ ，如图6)。由图5可知图中除了顶点2，3，23为2度点外，其余均为3度点。由图6可知图中除了顶点1，3，8为2度点外，其余均为3度点。

Figure 4. $FQCC\left(2,1\right)$

图4. $FQCC\left(2,1\right)$

Figure 5. Subgraph 1 of $FQCC\left(2,1\right)$

图5. $FQCC\left(2,1\right)$ 的子图1

Figure 6. Subgraph 2 of $FQCC\left(2,1\right)$

图6. $FQCC\left(2,1\right)$ 的子图2

假设 $G_b$ 与 $G_c$ 同构，即 $\varphi \left(b_i\right)=c_i\left(\forall b_i\in V\left(G_b\right),\forall c_i\in V\left(G_c\right)\right)$

情形1：若 $\varphi \left(3\right)=3$ ， $\varphi \left(2\right)=1$ ， $\varphi \left(23\right)=8$ 。则 $\varphi \left(4\right)=4$ ， $\varphi \left(6\right)=5$ 或6， $\varphi \left(8\right)=23$ ， $\varphi \left(7\right)=22$ 或24。顶点6和7在 $G_b$ 中相连，由同构定义得 $\varphi \left(6\right)$ 和 $\varphi \left(7\right)$ 相连，但在 $G_c$ 中5和22，24不相连，6和22，24不相连。所以此种情况不成立。

情形2：若 $\varphi \left(3\right)=1$ ， $\varphi \left(2\right)=3$ ， $\varphi \left(23\right)=8$ 。则 $\varphi \left(4\right)=23$ ， $\varphi \left(6\right)=22$ 或24， $\varphi \left(8\right)=4$ ， $\varphi \left(7\right)=5$ 或6。顶点6和7在 $G_b$ 中相连，由同构定义得 $\varphi \left(6\right)$ 和 $\varphi \left(7\right)$ 相连，但在 $G_c$ 中5和22，24不相连，6和22，24不相连。所以此种情况不成立。

情形3：若 $\varphi \left(2\right)=8$ ， $\varphi \left(3\right)=3$ ， $\varphi \left(23\right)=1$ 。在 $G_b$ 中顶点23和22，24相连。在 $G_c$ 中顶点1和3，23相连。则 $\{\begin{array}{l}\varphi \left(22\right)=23\\ \varphi \left(44\right)=3\end{array}$ 或 $\{\begin{array}{l}\varphi \left(22\right)=3\\ \varphi \left(44\right)=23\end{array}$ ，则在 $G_b$ 中顶点22和24之间有一条1长的路，而在 $G_c$ 中顶点3和23之间没有1长的路。所以此种情形不成立。

情形4：若 $\varphi \left(2\right)=3$ ， $\varphi \left(3\right)=8$ ， $\varphi \left(23\right)=1$ 。与情形3类似，所以此种情形不成立。

情形5：若 $\varphi \left(2\right)=1$ ， $\varphi \left(3\right)=8$ ，相连。在 $G_c$ 中顶点3和4，1相连。则 $\{\begin{array}{l}\varphi \left(22\right)=1\\ \varphi \left(44\right)=4\end{array}$ 或 $\{\begin{array}{l}\varphi \left(22\right)=4\\ \varphi \left(44\right)=1\end{array}$ ，则在 $G_b$ 中24和22之间有一条1长的路，而在 $G_c$ 中4和1之间没有一条1长的路。所以此种情形不成立。

情形6：若 $\varphi \left(2\right)=8$ ， $\varphi \left(3\right)=1$ ， $\varphi \left(23\right)=3$ 。与情形5类似，所以此种情形不成立。

综上所述：上述情形均不成立。 $G_b$ 和 $G_c$ 不同构。所以 $FQCC\left(2,1\right)$ 不是点可迁的。

3.3. FQCC(n,k)的点可迁性

在这一节中，赵媛讨论了 $FQCC\left(3,1\right)$ ， $FQCC\left(4,1\right)$ ， $FQCC\left(5,1\right)$ 以及 $FQCC\left(n,k\right)\left(k>1\right)$ 的点可迁性。

定理7： $FQCC\left(3,1\right)$ 不是点可迁的。

证明：为了方便书写，我们将图7 (图7是 $FQCC\left(3,1\right)$ 的部分子图)中的各顶点简记为1~15。不失一般性，我们在图7中删去顶点1 (记为 $G_h$ ，如图8)，在图7中删去顶点2 (记为 $G_m$ ，如图9)。由图8可知图中除了顶点2，3，13为2度点外，其余均为3度点。由图9可知图中除了顶点1，3，11为2度点外，其余均为3度点。

假设 $G_h$ 和 $G_m$ 同构，则 $\varphi \left(h_i\right)=m_i\left(\forall h_i\in V\left(G_h\right),\forall m_i\in V\left(G_m\right)\right)$ 。

情形1：若 $\varphi \left(2\right)=1$ ， $\varphi \left(3\right)=3$ ， $\varphi \left(13\right)=11$ 。则 $\varphi \left(4\right)=4$ ， $\varphi \left(6\right)=5$ 或6， $\varphi \left(11\right)=13$ ， $\varphi \left(10\right)=14$

或15。在 $G_h$ 中6和10之间有一条3长的路，而在 $G_m$ 中5和14，15之间没有一条3长的路，所以此种情形不成立。

情形2：若 $\varphi \left(2\right)=3$ ， $\varphi \left(3\right)=1$ ， $\varphi \left(13\right)=11$ 。则 $\varphi \left(4\right)=13$ ， $\varphi \left(6\right)=14$ 或15， $\varphi \left(11\right)=4$ ， $\varphi \left(10\right)=5$ 或6。

Figure 7. Part of subgraph of $FQCC\left(3,1\right)$

图7. $FQCC\left(3,1\right)$ 的部分子图

Figure 8. Part of subgraph 1 of $FQCC\left(3,1\right)$

图8. $FQCC\left(3,1\right)$ 的部分子图1

Figure 9. Part of subgraph 2 of $FQCC\left(3,1\right)$

图9. $FQCC\left(3,1\right)$ 的部分子图2

则在 $G_h$ 中6和10之间有一条3长的路，而在 $G_m$ 中14和5，6之间没有一条3长的路，15和5，6之间没有一条3长的路。所以此种情形不成立。

情形3：若 $\varphi \left(2\right)=1$ ， $\varphi \left(3\right)=11$ ， $\varphi \left(13\right)=3$ 。在 $G_h$ 中顶点3和2，4相连。在 $G_m$ 中顶点11和10，12相连。则 $\{\begin{array}{l}\varphi \left(2\right)=10\\ \varphi \left(4\right)=12\end{array}$ 或 $\{\begin{array}{l}\varphi \left(2\right)=12\\ \varphi \left(4\right)=10\end{array}$ ，则在 $G_h$ 中2和4之间没有一条1长的路，而在 $G_m$ 中10和12之间有一条1长的路。所以此种情形不成立。

情形4：若 $\varphi \left(2\right)=3$ ， $\varphi \left(3\right)=11$ ， $\varphi \left(13\right)=1$ 。与情形3类似，所以此种情形不成立。

情形5：若 $\varphi \left(2\right)=11$ ， $\varphi \left(3\right)=1$ ， $\varphi \left(13\right)=3$ 。在 $G_h$ 中顶点2和3，11相连。在 $G_m$ 中顶点11和10，12相连。则 $\{\begin{array}{l}\varphi \left(3\right)=10\\ \varphi \left(11\right)=12\end{array}$ 或 $\{\begin{array}{l}\varphi \left(3\right)=12\\ \varphi \left(11\right)=10\end{array}$ ，则在 $G_h$ 中3和11之间没有一条1长的路，在 $G_m$ 中10和12之间有一条1长的路。所以此种情形不成立。

情形6：若 $\varphi \left(2\right)=11$ ， $\varphi \left(3\right)=3$ ， $\varphi \left(13\right)=1$ 。与情形5类似，所以此种情形不成立。

综上所述，上述情况均不成立。 $G_h$ 和 $G_m$ 不同构。所以 $FQCC\left(3,1\right)$ 不是点可迁的。

定理8： $FQCC\left(4,1\right)$ 不是点可迁的。

证明：为了方便书写，我们将图10 (图10是 $FQCC\left(4,1\right)$ 的部分子图)中的各顶点简记为1~18。不失一般性，我们在图10中删去顶点1 (记为 $G_n$ ，如图11)，在图10中删去顶点2 (记为 $G_q$ ，如图12)。由图11可知图中除了顶点2，3，16为2度点外，其余均为3度点。由图12可知图中除了顶点1，3，14为2度点外，其余均为3度点。

假设 $G_n$ 和 $G_q$ 同构，则 $\varphi \left(n_i\right)=q_i\left(\forall n_i\in V\left(G_n\right),\forall q_i\in V\left(G_q\right)\right)$

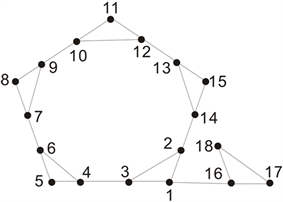
Figure 10. Part of subgraph of $FQCC\left(4,1\right)$

图10. $FQCC\left(4,1\right)$ 的部分子图

Figure 11. Part of subgraph 1 of $FQCC\left(4,1\right)$

图11. $FQCC\left(4,1\right)$ 的部分子图1

Figure 12. Part of subgraph 2 of $FQCC\left(4,1\right)$

图12. $FQCC\left(4,1\right)$ 的部分子图2

情形1：若 $\varphi \left(2\right)=1$ ， $\varphi \left(3\right)=3$ ， $\varphi \left(16\right)=14$ 。则 $\varphi \left(4\right)=4$ ， $\varphi \left(6\right)=5$ 或6， $\varphi \left(14\right)=16$ ， $\varphi \left(13\right)=17$ 或18。在 $G_n$ 中6和13之间有两条5长的路，而在 $G_q$ 中5和17，18之间只有一条5长的路，6和17，18之间只有一条5长的路。所以此种情形不成立。

情形2：若 $\varphi \left(2\right)=3$ ， $\varphi \left(3\right)=1$ ， $\varphi \left(16\right)=14$ 。则 $\varphi \left(4\right)=16$ ， $\varphi \left(6\right)=17$ 或18， $\varphi \left(14\right)=4$ ， $\varphi \left(13\right)=5$ 或6。则在 $G_n$ 中6和13之间有两条5长的路，而在 $G_q$ 中5和17，18之间只有一条5长的路，6和17，18之间只有一条5长的路。所以此种情形不成立。

情形3：若 $\varphi \left(2\right)=1$ ， $\varphi \left(3\right)=14$ ， $\varphi \left(16\right)=3$ 。则在 $G_n$ 中16和17，18相连。在 $G_q$ 中3和1，4相连。则 $\{\begin{array}{l}\varphi \left(17\right)=1\\ \varphi \left(18\right)=4\end{array}$ 或 $\{\begin{array}{l}\varphi \left(17\right)=4\\ \varphi \left(18\right)=1\end{array}$ ，则在 $G_n$ 中17和18之间有一条1长的路，而在 $G_q$ 中1和4之间没有一条1长的路。所以此种情形不成立。

情形4：若 $\varphi \left(2\right)=14$ ， $\varphi \left(3\right)=1$ ， $\varphi \left(16\right)=3$ 。与情形3类似，所以此种情形不成立。

情形5：若 $\varphi \left(2\right)=3$ ， $\varphi \left(3\right)=14$ ， $\varphi \left(16\right)=1$ 。在 $G_n$ 中顶点16和17，18相连。在 $G_q$ 中1和3，16相连。则 $\{\begin{array}{l}\varphi \left(17\right)=3\\ \varphi \left(18\right)=16\end{array}$ 或 $\{\begin{array}{l}\varphi \left(17\right)=16\\ \varphi \left(18\right)=3\end{array}$ ，则在 $G_n$ 中17和18之间有一条1长的路，而在 $G_q$ 中3和16之间没有一条1长的路。所以此种情形不成立。

情形6：若 $\varphi \left(2\right)=14$ ， $\varphi \left(3\right)=3$ ， $\varphi \left(16\right)=1$ 。与情形5类似，所以此种情形不成立。

综上所述，上述情况均不成立。 $G_n$ 和 $G_q$ 不同构。所以 $FQCC\left(4,1\right)$ 不是点可迁的。

定理9： $FQCC\left(5,1\right)$ 不是点可迁的。

证明：为了方便书写，我们将图13 (图10是 $FQCC\left(5,1\right)$ 的部分子图)中的各顶点简记为1~21。不失一般性，我们在图13中删去顶点1 (记为 $G_r$ ，如图14)，在图13中删去顶点2 (记为 $G_s$ ，如图15)。由图14

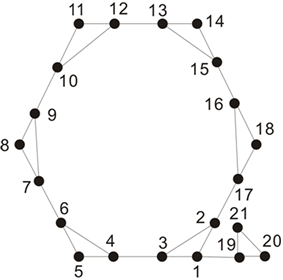
Figure 13. Part of subgraph of $FQCC\left(5,1\right)$

图13. $FQCC\left(5,1\right)$ 的部分子图

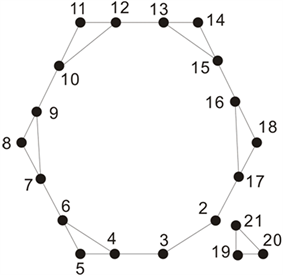
Figure 14. Part of subgraph 1 of $FQCC\left(5,1\right)$

图14. $FQCC\left(5,1\right)$ 的部分子图1

Figure 15. Part of subgraph 2 of $FQCC\left(5,1\right)$

图15. $FQCC\left(5,1\right)$ 的部分子图2

可知图中除了顶点2，3，19为2度点外，其余均为3度点。由图15可知图中除了顶点1，3，17为2度点外，其余均为3度点。

假设 $G_r$ 和 $G_s$ 同构，则 $\varphi \left(r_i\right)=s_i\left(\forall r_i\in V\left(G_r\right),\forall s_i\in V\left(G_s\right)\right)$

情形1：若 $\varphi \left(2\right)=1$ ， $\varphi \left(3\right)=3$ ， $\varphi \left(19\right)=17$ 。则 $\varphi \left(4\right)=4$ ， $\varphi \left(6\right)=5$ 或6， $\varphi \left(17\right)=19$ ， $\varphi \left(16\right)=20$ 或21。则在 $G_r$ 中6和16之间有两条7长的路，而在 $G_s$ 中5和20，21之间只有一条7长的路，6和20，21之间只有一条7长的路。所以此种情形不成立。

情形2：若 $\varphi \left(2\right)=3$ ， $\varphi \left(3\right)=1$ ， $\varphi \left(19\right)=17$ 。则 $\varphi \left(4\right)=19$ ， $\varphi \left(6\right)=20$ 或21， $\varphi \left(17\right)=4$ ， $\varphi \left(16\right)=5$ 或6。则在中6和16之间有两条7长的路，而在 $G_s$ 中5和20，21之间只有一条7长的路，6和20，21之间只有一条7长的路。所以此种情形不成立。

情形3：若 $\varphi \left(2\right)=1$ ， $\varphi \left(3\right)=17$ ， $\varphi \left(19\right)=3$ 。在 $G_r$ 中顶点19和20，21相连。在 $G_s$ 中顶点3和1，4相连。则 $\{\begin{array}{l}\varphi \left(20\right)=1\\ \varphi \left(21\right)=4\end{array}$ 或 $\{\begin{array}{l}\varphi \left(20\right)=4\\ \varphi \left(21\right)=1\end{array}$ ，则在 $G_r$ 中20和21之间有一条1长的路，而在 $G_s$ 中1和4之间没有一条1长的路。所以此种情形不成立。

情形4：若 $\varphi \left(2\right)=17$ ， $\varphi \left(3\right)=1$ ， $\varphi \left(19\right)=3$ 。与情形3类似，所以此种情形不成立。

情形5：若 $\varphi \left(2\right)=3$ ， $\varphi \left(3\right)=17$ ， $\varphi \left(19\right)=1$ 。在 $G_r$ 中顶点19和20，21相连。在 $G_s$ 中顶点1和3，19相连。则 $\{\begin{array}{l}\varphi \left(20\right)=3\\ \varphi \left(21\right)=19\end{array}$ 或 $\{\begin{array}{l}\varphi \left(20\right)=19\\ \varphi \left(21\right)=3\end{array}$ ，则在 $G_r$ 中20和21之间有一条1长的路，而在 $G_s$ 中3和19之间没有1长的路。所以此种情形不成立。

情形6：若 $\varphi \left(2\right)=17$ ， $\varphi \left(3\right)=3$ ， $\varphi \left(19\right)=1$ 。与情形5类似，所以此种情形不成立。

综上所述，上述情况均不成立。 $G_r$ 和 $G_s$ 不同构。所以 $FQCC\left(5,1\right)$ 不是点可迁的。

定理10： $FQCC\left(n,k\right)\left(k\ge 2\right)$ 不是点可迁的。

证明：为了方便书写，我们将图16中的各顶点简记为1~12。当 $n=2$ 且 $k=1$ 时结论显然成立。当 $n\ge 3,k\ge 2$ 时，一定有 $FQCC\left(n,k\right)$ 的子图。不失一般性，我们在图16中删去顶点1 (记为 $G_t$ ，如图17)，在图16中删去顶点2 (记为 $G_w$ ，如图18)。由图17可知图中除了顶点2，3，11为2度点外，其余均为3度点。由图18可知图中除了顶点1，3，8为2度点外，其余均为3度点。

假设 $G_t$ 和 $G_w$ 同构，则 $\varphi \left(t_i\right)=w_i\left(\forall t_i\in V\left(G_t\right),\forall w_i\in V\left(G_w\right)\right)$ 。

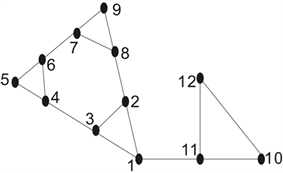
Figure 16. Part of subgraph of $FQCC\left(n,k\right)$

图16. $FQCC\left(n,k\right)$ 的部分子图

Figure 17. Part of subgraph 1 of $FQCC\left(n,k\right)$

图17. $FQCC\left(n,k\right)$ 的部分子图1

Figure 18. Part of subgraph 2 of $FQCC\left(n,k\right)$

图18. $FQCC\left(n,k\right)$ 的部分子图2

情形1：若 $\varphi \left(3\right)=3$ ， $\varphi \left(2\right)=8$ ， $\varphi \left(11\right)=1$ 。在 $G_t$ 中顶点11和10，12相连。在 $G_w$ 中顶点1和3，11相连。则 $\{\begin{array}{l}\varphi \left(12\right)=3\\ \varphi \left(10\right)=11\end{array}$ 或 $\{\begin{array}{l}\varphi \left(12\right)=11\\ \varphi \left(10\right)=3\end{array}$ ，则在 $G_t$ 中10和12之间有一条1长的路，而在 $G_w$ 中3和11之间没有一条1长的路。所以此种情形不成立。

情形2：若 $\varphi \left(3\right)=8$ ， $\varphi \left(2\right)=3$ ， $\varphi \left(11\right)=1$ 。与情形1类似，所以此种情形不成立。

情形3：若 $\varphi \left(3\right)=3$ ， $\varphi \left(2\right)=1$ ， $\varphi \left(11\right)=8$ 。则 $\varphi \left(4\right)=4$ ， $\varphi \left(6\right)=5$ 或6， $\varphi \left(8\right)=11$ ， $\varphi \left(7\right)=10$ 或12。在 $G_t$ 中顶点6和7相连，由同构定义得 $\varphi \left(6\right)$ 和 $\varphi \left(7\right)$ 相连。但在 $G_w$ 中顶点5和10，12不相连，6和10，12不相连。所以此种情形不成立。

情形4：若 $\varphi \left(3\right)=8$ ， $\varphi \left(2\right)=1$ ， $\varphi \left(11\right)=3$ 。在 $G_t$ 中顶点11和10，12相连。在 $G_w$ 中顶点3和4，1相连。则 $\{\begin{array}{l}\varphi \left(12\right)=4\\ \varphi \left(10\right)=1\end{array}$ 或 $\{\begin{array}{l}\varphi \left(12\right)=1\\ \varphi \left(10\right)=4\end{array}$ ，则在 $G_t$ 中10和12之间有一条1长的路，而在 $G_w$ 中4和1之间没有一条1长的路。所以此种情形不成立。

情形5：若 $\varphi \left(3\right)=1$ ， $\varphi \left(2\right)=8$ ， $\varphi \left(11\right)=3$ 。与情形4类似，所以此种情形不成立。

情形6：若 $\varphi \left(3\right)=1$ ， $\varphi \left(2\right)=3$ ， $\varphi \left(11\right)=8$ 。则 $\varphi \left(8\right)=4$ ， $\varphi \left(7\right)=5$ 或6， $\varphi \left(4\right)=11$ ， $\varphi \left(6\right)=10$ 或12。在 $G_t$ 中顶点6和7相连，由同构定义得 $\varphi \left(6\right)$ 和 $\varphi \left(7\right)$ 相连，但在 $G_w$ 中顶点5和10，12不相连，6和10，12不相连。所以此种情形不成立。

综上所述，上述情况均不成立。 $G_t$ 和 $G_w$ 不同构。所以 $FQCC\left(n,k\right)\left(k\ge 2\right)$ 不是点可迁的。

4. 结束语

我们证明了网络 $FQCC\left(2,k\right)\left(k\ge 0\right)$ 是平面的，Hamilton的，且 $FQCC\left(2,0\right)$ 是Hamilton连通的，但 $FQCC\left(n,1\right)\left(2\le n\le 5\right)$ 不是点可迁的且 $FQCC\left(n,k\right)\left(k\ge 2\right)$ 不是点可迁的。而 $FQCC\left(n,k\right)\left(n\ge 2,k\ge 0\right)$ 还有很多性质有待进一步研究。