关于完全π-正则半群类的禁止因子的注记

A Note on the Forbidden Epidivisors of Some Subclasses of Epigroups

摘要: 完全π-正则半群是其所含任意元的某个幂属于其最大子群的半群。论文在给出核为完全正则半群的完全π-正则半群类的刻画基础上，利用禁止因子和等式刻画了该型半群的推广类。同时讨论核为带的完全π-正则半群的特殊情形。

Abstract: A semigroup is called an epigroup if for each element in this given semigroup, some power of the element lies in some subgroup of the given semigroup. In this paper based on the given characterizations of epigroups in which the idempotent-generated subsemigroups are completely regular, we give some descriptions of some subclasses of epigroups in terms of identities, and forbidden epidivisors. For a special case, epigroups in which the kernels are bands are also characterized.

1. 引言与预备知识

若半群 $S$ 中任意元 $x$ 的某个方幂 $x^n$ ( $n$ 为正整数)是属于该半群的最大子群 $G_x$ 中的群元，则该型半群 $S$ 称为完全p-正则半群。包含元 $x^n$ 的最大子群 $G_x$ 的单位元记作 $x^{\omega }$ 。易知 $x{x}^{\omega }=x^{\omega }x$ ，且 $x^{\omega }x$ 是 $G_x$ 中的群元，其在 $G_x$ 中的群逆元记为 $\bar{x}$ 。映射 $x\to \bar{x}$ 称作是 $S$ 上的伪逆运算。此类半群可以看作是拥有一元伪逆运算和二元半群乘法运算的(2,1)-代数，记为 $E$ 。文献 [1] [2] 致力于研究完全p-正则半群的结构性理论(也见 [3] )。在刻画完全p-正则半群的某一子类(简称完全p-正则半群类)时，可以利用其满足的等式来表示该类半群，即利用等式给出一些完全p-正则半群类等价刻画。为简写需要，在给出完全p-正则子半群类的满足等式时，采用习惯记号，用字母 $e,f$ 表示形如 $x^{\omega },y^{\omega }$ 的一元运算，其中 $x,y$ 不出现在 $e,f$ 中。如等式 ${\left(exf\right)}^{\omega +1}=exf$ 是 $y^{\omega }x{z}^{\omega }{\left(y^{\omega }x{z}^{\omega }\right)}^{\omega }=y^{\omega }x{z}^{\omega }$ 的缩写，其中 $x,y$ 和 $z$ 为互异变量。

在刻画完全p-正则半群类时，还可以利用其禁止因子来确定该类半群。所谓禁止因子，就是在研究该类半群的完全p-正则子半群的同态象(称为因子)时，通过排除一些具体的熟知半群来刻画该类半群，而这些排除的半群可以用一些结构和性质都很清晰的完全p-正则半群来表示，这样的半群就称作该类半群的禁止因子。研究完全p-正则半群类的禁止因子有其理论及其实践上的意义。关于完全p-正则半群禁止因子的研究在文献 [1] - [6] 中都有论述。本文在给出幂等元生成半群(称之为核)为完全正则的完全p-正则半群类的刻画基础上，主要研究一些完全p-正则半群类的基本性质和构造特点，寻找结构清晰且具有良好表示的一些具体禁止因子半群，通过这些禁止因子来给出该类半群的等价刻画。同时讨论核为带的完全p-正则半群的特殊情形。文中 $L_2,R_2$ 分别表示二元左零半群和二元右零半群，其他后文用到的禁止因子半群表示如下：

$\begin{array}{l}V=\langle e,f|e^2=e,f^2=f,fe=0\rangle ;\\ F=\langle e,f|e^2=e,f^2=f,fef=0\rangle ;\\ M_n=\langle e,f|e^2={\left(efe\right)}^n=e,f^2={\left(fef\right)}^n=f\rangle \end{array}$

其中半群 $M_n$ 同构于Rees 矩阵半群 $\mathcal{M}\left[2,C_{1,n},2;\left(\begin{array}{cc}\epsilon & \epsilon \\ \epsilon & \gamma \end{array}\right)\right]$ ， $\epsilon$ 为单位元， $\gamma$ 为循环群 $C_{1,n}$ 的生成元。

还需说明的是完全p-正则半群的因子是可传递的，即对 $S,T,U\in E$ ，若 $T$ 是 $S$ 的因子， $U$ 是 $T$ 的因子，则 $U$ 是 $S$ 的因子。

本文所用半群记号和术语详见参考文献 [7] [8] [9] 。下面给出本文需要的部分预备知识。

若半群 $S$ 不含幺元，我们为 $S$ 添加新符号1，使得对任意 $s\in S\cup \left\{1\right\}$ ， $1s=s1=s$ 。这样得到的幺半群记为 $S^1$ ；若半群 $S$ 含幺元，定义 $S^1=S$ 。对 $e\in S$ ，若 $e^2=e$ ，称 $e$ 是 $S$ 中的幂等元。若 $a$ 属于 $S$ 的一个子群，则称 $a$ 是 $S$ 中的群元。若 $I$ 为半群 $S$ 的一个理想(即 $IS\cup SI\subseteq I$ )，则 $S/I$ 表示半群 $S$ 的Rees商。设 $A$ 与 $B$ 为 $S$ 的两个子集，集合 $\left\{x\in A|x\notin B\right\}$ 记为 $A\backslash B$ 。

关系 $\mathcal{J},\mathcal{L},\mathcal{R},\mathcal{D}$ 和 $\mathcal{H}$ 表示半群 $S$ 上的Green关系，包含元 $a$ 的 $\mathcal{D}$ -类记作 $D_a$ ，类似可记 $J_a,R_a,L_a$ 及 $H_a$ 。在完全p-正则半群中，等式 $\mathcal{J}=\mathcal{D}$ 成立。

令 $S$ 为完全p-正则半群。对子集 $X\subseteq S$ ， $\langle X\rangle$ 表示由 $X$ 生成的 $S$ 的子半群，而 $\langle \langle X\rangle \rangle$ 为由 $X$ 生成的 $S$ 的完全p-正则子半群。后者一元半群项(an epigroup term over $X$ )记为 $t\left(X\right)$ 。为证明需要，用递归法定义一元半群项 $t\in \langle \langle X\rangle \rangle$ 的长度 $d\left(t\right)$ ：若 $t\in X$ ， $d\left(t\right)=0$ ；若 $t_1,t_2\in \langle \langle X\rangle \rangle$ 使得 $d\left(t_1\right)=m,d\left(t_2\right)=n$ ，则 $d\left(t_1{t}_2\right)=m+n,d\left(\overline{t_1}\right)=m+1$ 。 $S$ 的幂等元集记为 $E_S$ ，其生成子半群 $\langle E_S\rangle$ 为 $S$ 的核。注意由 [3] 引理2.6， $\langle \langle E_S\rangle \rangle =\langle E_S\rangle$ 。

对于完全p-正则半群类，可以应用某些具体运算来构造一些新类。例如，对于完全p-正则半群类 $V$ ，令

$\begin{array}{l}C\left(V\right)=\left\{S\in E|\langle E_S\rangle \in V\right\},\\ L\left(V\right)=\left\{S\in E|eSe\in V,\forall e\in E_S\right\}\end{array}$

可见 $C\left(V\right)$ 恰由核属于 $V$ 的完全p-正则半群组成，而 $L\left(V\right)$ 恰由局部属于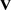的完全p-正则半群组成。

由 [10] 定理6.45和 [8] 定理2.2.5，易得下述结论。

引理1.1. 令 $S$ 为完全p-正则半群， $a\in S$ 。若 $a\mathcal{D}{a}^2$ ，则 $a$ 为群元。

2. 主要结论

2.1. 核为完全正则半群的完全p-正则半群

作为完全p-正则半群类，完全正则半群是群的并，该类半群记作 $CR$ 。完全正则半群的另一重要刻画是其为完全单半群的半格。完全正则半群 $S$ 上的Green关系 $\mathcal{D}$ 是唯一的幂等元同余类为完全单半群的半格同余。下面的定理来自 [5] 定理3.1。

定理2.1. 完全p-正则半群 $S$ 上的下列条件等价：

1) $S\in C\left(CR\right)$ ；

2) $S$ 满足等式 ${\left(x^{\omega }{y}^{\omega }\right)}^{\omega +1}=x^{\omega }{y}^{\omega }$ ；

3) $S$ 不含因子 $V$ 。

上述定理的结果是下文进一步研究的基础。

2.2. 两个定理及其证明

我们先来看定理2.1的第一个推广，有如下定理。

定理2.2. 完全p-正则半群 $S$ 上的下列条件等价：

1) $S\in LC\left(CR\right)$ ；

2) $S$ 满足等式 ${\left({\left(exe\right)}^{\omega }{\left(eye\right)}^{\omega }\right)}^{\omega +1}={\left(exe\right)}^{\omega }{\left(eye\right)}^{\omega }$ ；

3) $S$ 不含因子 $V^1$ 。

证明：1) Û 2)。事实上，由定理2.1，

$\begin{array}{l}S\in LC\left(CR\right)\iff \left[\forall e\in E_S\right]eSe\in C\left(CR\right)\\ \iff \left[\forall e\in E_S\right]\langle E_{eSe}\rangle \in C\left(CR\right)\\ \iff \left[\forall e\in E_S,\forall x,y\in S\right]{\left({\left(exe\right)}^{\omega }{\left(eye\right)}^{\omega }\right)}^{\omega +1}={\left(exe\right)}^{\omega }{\left(eye\right)}^{\omega }\end{array}$

2) Û 3)。若 $S$ 满足2)中等式，则其因子满足该等式，显然 $V^1$ 不满足该等式，从而 $V^1$ 不是 $S$ 的因子。

对于“3) Þ 2)”的证明，我们采用反证法，参考 [11] 命题1.2的证明过程，这儿给出证明概要。若 $S$ 不满足3)中等式，则存在 $e\in E_S$ ， $a,b\in S$ 使得 ${\left({\left(eae\right)}^{\omega }{\left(ebe\right)}^{\omega }\right)}^{\omega +1}\ne {\left(eae\right)}^{\omega }{\left(ebe\right)}^{\omega }$ ，也即 ${\left(eae\right)}^{\omega }{\left(ebe\right)}^{\omega }$ 不是群元。不妨令 $S_0=\langle \langle e,{\left(eae\right)}^{\omega },{\left(ebe\right)}^{\omega }\rangle \rangle$ ，可以证明

$S_0=\left\{e,{\left(eae\right)}^{\omega },{\left(ebe\right)}^{\omega },{\left(eae\right)}^{\omega }{\left(ebe\right)}^{\omega }\right\}\cup {\left(ebe\right)}^{\omega }{\left(eae\right)}^{\omega }{S}_0\cup {\left(eae\right)}^{\omega }{\left(ebe\right)}^{\omega }{\left(eae\right)}^{\omega }{S}_0$

令 $I={\left(ebe\right)}^{\omega }{\left(eae\right)}^{\omega }{S}_0\cup {\left(eae\right)}^{\omega }{\left(ebe\right)}^{\omega }{\left(eae\right)}^{\omega }{S}_0$ ，因为 ${\left(eae\right)}^{\omega }{\left(ebe\right)}^{\omega }$ 不是群元，可以证明 ${\left(eae\right)}^{\omega }{\left(ebe\right)}^{\omega }\notin I$ ，且 $e,{\left(eae\right)}^{\omega },{\left(ebe\right)}^{\omega }$ 和 ${\left(eae\right)}^{\omega }{\left(ebe\right)}^{\omega }$ 两两互异，从而 $S_0/I\simeq V^1$ 。这样 $S_0$ 含因子 $V^1$ ，当然 $S$ 亦含因子 $V^1$ ，这就与条件3)矛盾，从而结论得证。

接下来考查用等式来表示的一类完全p-正则半群，显然该类半群不仅包含 $C\left(CR\right)$ ，还包含 $CL\left(CR\right)$ 。这儿我们更关心其禁止因子的刻画。

定理2.3. 完全p-正则半群 $S$ 上的下列条件等价：

1) $S$ 满足等式 $\overline{{\left(ef\right)}^{\omega }{\left(fe\right)}^{\omega }}=efe$ ；

2) $S$ 满足等式 ${\left(efe\right)}^{\omega +1}=efe$ ；

3) $S$ 不含因子 $F$ 。

证明：1) Û 2)。事实上， ${\left(efe\right)}^{\omega +1}=\overline{\stackrel{¯}{efe}}$ 。另一方面，结合 [4] 中等式(4)及其推论，有

$\overline{efe}=e\overline{fe}=e{\left(fe\right)}^{\omega }\overline{fe}={\left(ef\right)}^{\omega }e\overline{fe}={\left(ef\right)}^{\omega }fe\overline{fe}={\left(ef\right)}^{\omega }{\left(fe\right)}^{\omega }$

由上述事实，显然充要性成立。

2) Û 3)。若 $S$ 满足2)中等式，则其因子也满足该等式，显然 $F$ 不满足该等式，从而 $F$ 不是 $S$ 的因子。

对于“3) Þ 2)”的证明，这儿亦采用反证法。若 $S$ 不满足2)中等式，则有 $e,f\in E_S$ 使得 ${\left(efe\right)}^{\omega +1}\ne efe$ ，也即 $efe$ 不是群元(可以证明，此时 $ef,fe$ 亦非群元)。既然因子可传递，不妨令 $S=\langle \langle e,f\rangle \rangle$ 。

首先来证

$S=\left\{e,f,ef,fe,efe\right\}\cup fefS\cup efefS$ (1)

记 $I=fefS\cup efefS$ ， $T=\left\{e,f,ef,fe,efe\right\}\cup fefS\cup efefS$ 。显然只需证 $S\subseteq T$ 。

考虑 $S$ 中的一元半群项 $t\left(e,f\right)$ (简记为 $t$ )，其中 $d\left(t\right)=n$ 。应用数学第二归纳法来证明 $t\in T$ 。

若 $d\left(t\right)=0$ ，即 $t\in \left\{e,f\right\}$ ，则 $t\in T$ 。

考察情形 $t=t_1{t}_2$ ，则 $d\left(t_1\right),d\left(t_2\right)<n$ ，由归纳假设， $t_1,t_2\in T$ 。再分情况讨论。若 $t_1\in I$ ，显然 $t\in I$ ；若 $t_1=\left\{e,f,ef,fe,efe\right\}$ ， $t_2\in I$ ，易得 $t=t_1{t}_2\in I$ ；若 $t_1,t_2\in \left\{e,f,ef,fe,efe\right\}$ ，则

$t=t_1{t}_2\in \left\{e,f,ef,fe,efe,fef,fefe,efef,efefe\right\}\in T$

考察情形 $t=\bar{u}$ ，其中 $d\left(u\right)=n-1,n\ge 1$ 。由归纳假设 $u\in T$ 。注意到 $t=\bar{u}=u{\left(\bar{u}\right)}^2$ 。若 $u\in I$ ，则 $t\in I$ ；若 $u\in \left\{e,f\right\}$ ，亦有 $t\in \left\{e,f\right\}$ ；若 $u\in \left\{ef,fe,efe\right\}$ ，注意到 $t=\bar{u}=u^2{\left(\bar{u}\right)}^3$ ，可以证明 $t\in I$ 。

由上述各情形的证明，等式(1)成立。同时易证 $SI\cup IS\subseteq I$ ，即 $I$ 是 $S$ 的理想。

其次，我们来证 $efe\notin I$ 。用反证法，若 $efe\in I$ ，则有 $efe\in fefS$ 或 $efe\in efefS$ ，既然前者蕴含后者，只考虑 $efe\in efefS$ 。此时存在 $s\in S$ 使得 $efe=efefs$ 。若 $s\in S\backslash \left\{f\right\}$ ，则 $efe\in efefeS$ ，此时必有 $efe\mathcal{D}{\left(efe\right)}^2$ ，由引理1.1， $efe$ 为群元，矛盾；若 $s=f$ ，即 $efe=efef$ ，在该等式等号两边右乘 $e$ ，得 $efe=efefe$ ，故 $efe$ 为幂等元，矛盾。这样 $efe\notin I$ 得证，从而亦有 $e,f,ef,fe\notin I$ 。

最后，可证 $e,f,ef,fe$ 和 $efe$ 两两互异。否则得到 $efe$ 为群元，矛盾。例如，若有 $efe=fe$ ，则

$efefe=fe\cdot fe=f\cdot fe=fe=efe$

这样 $efe$ 为幂等元，矛盾。

综合以上，易知Rees商 $S/I\simeq F$ 。从而 $S$ 含因子 $F$ ，与条件2)矛盾。

3. 核为带的完全p-正则半群

下面讨论定理2.1所给半群类 $C\left(CR\right)$ 的特殊情形。若半群中任意元都是幂等元，这样的半群称作带，记作 $B$ 。交换带称作半格，记作 $S$ 。

命题3.1. 完全p-正则半群 $S$ 上的下列条件等价：

1) $S\in C\left(B\right)$ ；

3) $S$ 满足等式 ${\left(x^{\omega }{y}^{\omega }\right)}^{\omega }=x^{\omega }{y}^{\omega }$ ；

3) $S$ 不含因子 $V$ 和 $M_p$ ， $p$ 为任意素数。

证明：1) Þ 2)。若1)成立，则 $\langle E_S\rangle \subseteq E_S$ ，从而对任意 $x,y\in S$ ， $x^{\omega }{y}^{\omega }\in E_S$ ，即 ${\left(x^{\omega }{y}^{\omega }\right)}^{\omega }=x^{\omega }{y}^{\omega }$ 。这样证得2)成立。

2) Þ 3)。若2)成立，则 $\langle E_S\rangle =E_S$ 是带，从而 $S\in C\left(CR\right)$ 。由定理2.1， $S$ 不含因子 $V$ 。若 $S$ 含因子 $M_p$ ，其中 $p\ge 2$ 为某一素数。此时对 $e,f\in M_p$ ，必有 ${\left(ef\right)}^2\ne ef$ 。另一方面，因为 $M_p$ 是 $S$ 的因子，则存在 $S$ 的完全p-正则子半群 $T$ 和满同态 $\phi :T\to V$ 。由 [7] 推论1.4.9，有 $e^{\prime },f^{\prime }\in E_T$ 使得 $e^{\prime }\phi =e,f^{\prime }\phi =f$ 。注意到 $E_T$ 亦是带，这样

$ef=e^{\prime }\phi f^{\prime }\phi =\left(e^{\prime }{f}^{\prime }\right)\phi ={\left(e^{\prime }{f}^{\prime }\right)}^2\phi ={\left(\left(e^{\prime }{f}^{\prime }\right)\phi \right)}^2={\left(ef\right)}^2$

此与前述 ${\left(ef\right)}^2\ne ef$ 矛盾。由此证得 $S$ 不含因子 $M_p$ ， $p$ 为任意素数。

3) Þ 1)。若3)成立，则由定理2.1， $\langle E_S\rangle$ 为完全正则子半群。另一方面， $S$ 不含因子 $M_p$ ( $p$ 为任意素数)，由 [2] 引理9， $S$ 不含因子 $M_n$ ( $n$ 为任意正整数或为无穷大)。从而 $\langle E_S\rangle$ 亦不含因子 $M_n$ ( $n$ 为任意正整数或为无穷大)。由 [9] 推论III.5.5 $\langle E_S\rangle$ 的幂等元集合为子半群，从而 $\langle E_S\rangle =E_S$ ，即 $S\in C\left(B\right)$ 。

命题3.2. 完全p-正则半群 $S$ 上的下列条件等价：

1) $S\in C\left(S\right)$ ；

2) $S$ 满足等式 $x^{\omega }{y}^{\omega }=y^{\omega }{x}^{\omega }$ ；

3) $S$ 不含因子 $L_2,R_2$ 和 $V$ 。

证明：1) Û 2)。显然， $\langle E_S\rangle$ 是半格当且仅当对任意 $e,f\in E_S,ef=fe$ 。从而充要性得证。

2) Û 3)。若 $S$ 满足2)中等式，则其因子也满足该等式，显然3)中所列半群都不满足该等式，从而条件3)成立.

反之，若3)成立。由于 $L_2,R_2$ 为 $M_p$ ( $p$ 为任意素数)的因子，则 $S$ 不含因子 $V$ 和 $M_p$ ( $p$ 为任意素数)。从而由命题3.1， $\langle E_S\rangle =E_S$ 是带，为矩形带的半格(见 [9] 推论II.1.7)。再由 $S$ 不含因子 $L_2,R_2$ ，从而带 $E_S$ 亦不含因子 $L_2,R_2$ ，从而 $E_S$ 的 $\mathcal{D}$ -类皆平凡。这样 $E_S$ 为平凡带的半格，即半格。从而条件1)成立。

基金项目

临沂大学大学生创新创业训练计划项目资助(项目编号201710452003)。

NOTES

$$

^*通讯作者。