1. 引言
众所周知,全概率公式是《概率论与数理统计》课程中一个非常重要的公式。在大多数的教科书 [1] [2] 上,我们能看到详细的关于全概率公式的介绍及公式的推导。纵观以往的文献,也不难发现很多关于完备事件组的分解注释、这个公式的推广及其应用 [3] [4] [5] [6] ,教案设计、教学方法研究 [7] 等等,但是很少有文献讨论关于这一知识点的例子选择和收集。我们在教与学的过程中通常都会借助一些例子来加强对数学概念或公式的理解和运用,例如疾病检测就是一个被经常选入教科书的典型例子,因为例子是最直接最有效的学习载体,也是理解知识点的最佳途径。笔者在多年的教学过程中,参考了多本教材,发现全概率公式这一知识点的例子都比较中规中矩,主要注重对全概率公式的讲解和运用,但是相对都比较沉闷,学生在学习过程中缺乏兴趣和动力,主动性不高。因此,在本文中,我们收集整理了三个和全概率公式相关的生动有趣的问题或例子,供学生学习和理解这两个公式时借鉴,同时也能了解一些流传的经典案例,提高学习概率统计的积极性。
为了后续内容介绍的连贯性,首先,我们还是先简单阐述一下全概率公式的定义。
完备事件组的定义:设
是随机试验,
是相应的样本空间,
为事件组,若
满足条件:(1)
;(2)
,则称事件组
为样本空间的一个完备事件组。完备事件组完成了对样本空间的一个分割。同时也完成了对事件B的一个分割,见图1和图2。
全概率公式:设
为完备事件组,且
,
为任一事件,则
例如,当
时,即为
。下面的树图(图3)给出了全概率公式的分解。
2. 蒙提霍尔问题(Monty Hall Problem)
这是一个源自博弈论的数学游戏问题。这个概率问题也因为影片“决胜21点”中,主角班·坎贝尔(Ben Campbell)成功解开教授米基·罗沙(Mickey Rosa)在课上的提问而非常有名。影片中是这样描述的,有三扇关闭了的门A、B和C,其中一扇门后是一辆汽车(寓意价值高,是奖品),其他两扇门后各藏有一只山羊(寓意价值很低),Ben选了第一扇门A,然后教授Michey把第三扇门C打开了,后面是一只山羊。这时候教授Michey问Ben:“你换不换到第二扇门?”Ben的回答是:换。因为如果不换,赢得汽车的
概率是
;如果换,赢得汽车的概率将是
。
这样的回答似乎感觉上与我们的直观相悖,因为从直观上来说,既然已经知道C门后是羊,那么A门和B门一个后面是汽车,另一个后面是山羊,不管选A或B,选到汽车山羊的概率都是
。换句话说,这时候,换或不换,赢得汽车的概率都是
。事实上,如果Ben先选中的A门后是山羊,换后百分之百赢;如果A门后是汽车,换后百分之百输。而A门后是山羊的概率是
,A门后是汽车的概率是
。所以不管怎样都换,相对最初的赢得汽车仅为
的机率来说,转换选择可以增加赢的机会。
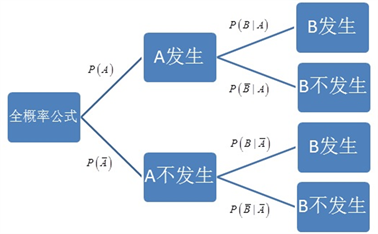
Figure 3. Tree diagram of full probability formula
图3. 全概率公式的树图分解
关于这个问题,我们可以查询到很多种解释方法,而借助全概率公式的解释是比较容易理解的一种解释方式。首先可以用树图(图4)来表示两个不同策略及其相应的概率值。
首先设
=“最初选择的门后是汽车”,
表示“最终赢得汽车”,则由已知条件知,实际情况中汽车在A门后的概率是
,不在A门后的概率是
,即
。
策略一:Ben不换选择,即仍然选择A门,则Ben能最终赢得汽车的概率,即
,
策略二:Ben换选择,即换至未开启的B门,则Ben能最终赢得汽车的概率,即
,
所以,显然,策略二即Ben换到未打开的B门,他能赢得汽车的概率将比不换增加一倍。
3. 辛普森悖论(Simpson’s paradox)
例如,有两种治疗肾结石的方案:方案1和方案2。在接受方案1治疗的所有患者中小结石患者占23%,大结石患者占77%,小结石患者的治愈率是93%,大结石患者的治愈率是73%。在接受方案2治疗的所有患者中小结石患者占67%,大结石患者占33%,小结石患者的治愈率是87%,大结石患者的治愈率是69%。如表1所示。
首先,我们发现不管是对小结石患者还是大结石患者,方案1的治愈率都要高于方案2,那么我们能就此判断方案1要优于方案2吗?
同样设
=“小结石患者”,
=“治愈”,
方案1:由已知条件可知:
,
则根据全概率公式,可得所有接受方案1的患者治愈率为:
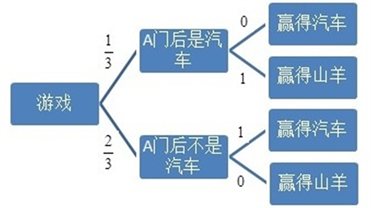
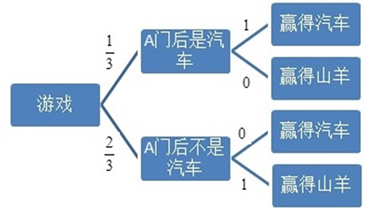 策略一:不换选择 策略二:换选择
策略一:不换选择 策略二:换选择
Figure 4. Tree diagram of Monty Hall Problem
图4. 蒙提霍尔问题策略树图

Table 1. Two treatments for kidney stone
表1. 两种治疗肾结石的方案
方案2:由已知条件可知:
,
则所有接受方案2的患者治愈率为:
,
所以,方案2的患者治愈率要比方案1高!这个结论大大出乎我们之前的直观结论。
究其原因,那是因为之前观察数据的时候,我们比较的是每种方案下,不同患者的治愈率,换句话说,我们比较的这些“治愈率”都是条件概率。
如果把不同患者定义成“原因”(
和
),治愈定义成“结果”(
)。也可以说,我们比较的是,在已知不同“原因”发生的条件下,“结果”发生的概率。而通过全概率公式的计算,最终我们只是比较“结果”发生概率的大小,这是综合了所有“原因”以后的一个结论。而各个“原因”在全概率公式计算中占有的权重直接影响了最终的概率结论,发生了所谓的“悖论”的出现!
4. 敏感性问题调查(sensitivity analysis)
对于考试作弊,赌博,偷税漏税,酒后驾车等一些涉及个人隐私或利害关系,不受被调查对象欢迎或感到尴尬的敏感问题,即使做无记名的直接调查,也很难消除被调查者的顾虑,他们极有可能拒绝应答或故意做出错误的回答,很难保证数据的真实性,使得调查的结果存在很大的误差。如何设计合理的调查方案,来提高应答率并降低不真实回答率呢?基于全概率公式的调查方案设计就能解决这个问题。
调查方案设计的基本思想是,让被调查者从
问题1:你在考试中曾经作弊过吗?
问题2:你生日的月份是奇数吗?(约定一年有365天)
这两个问题中,随机地选答其中一个,同时调查者并也不知情被调查者回答的是哪一个问题,从而保护被调查者的隐私,消除被调查者的顾虑,能够对自己所选的问题真实地回答。
调查者准备一套13张同一花色的扑克,在选答上述问题前,要求被调查的学生随机抽取一张,看后放回,调查者并不知道学生抽取的情况。约定如下:如果学生抽取的是不超过10的数则回答问题1;反之,则回答问题2。假定调查结果是收回400张有效答卷,其中有80个学生回答“是”,320个学生回答“否”,求被调查的学生考试作弊的概率
。
以
表示选答问题1,
表示回答“是”,
,则由已知条件知:
,
由全概率公式
,由此可算得
。
5. 结语
以上三个例子都是可以利用全概率公式来解决的著名经典问题,从全概率公式的讲解来看,简单易懂,相比目前的教材中多以盒子取球或掷骰子为背景的例题来说,趣味性大大增强,不失为课堂教学和活跃气氛的好例子,使得学生能轻松快速掌握全概率公式这个知识点,还有了利用概率统计方法解释现实中经典案例的直观体验,寓教于乐,提高学习积极性。