1. 引言
教学楼是学校内学生密集分布区域,在发生火灾、地震、以及其它重大安全事故等情况下,需要用尽可能短的时间对教学楼内的学生进行紧急疏散。学生在紧急疏散过程中的情绪恐慌、无序、拥挤、踩踏等众多因素往往导致疏散时间延长,降低疏散效率,甚至造成学生伤害。研究学生从教学楼的紧急疏散问题现实意义重大,但是,采取在教学楼内大规模组织学生多次进行真实紧急疏散实验来获取最优疏散路线和策略的方法,不仅成本高,而且也会影响学校的正常教学秩序。在这样的情形下,通过数值模拟研究学生从教学楼的紧急疏散问题就成为一种好的实行方案。
近年来,国内外学者运用数学模型和计算机仿真对紧急疏散问题进行了相关研究。Meiling Chu等 [1] 提出SAFEgress (社会代理出口)代理模型建立仿真平台,用来模拟不同居住者的行为。比如在校园建筑方面。Jack Guest等 [2] 采用修改heuristic-based疏散算法的变体重新设计了系统,使其能够处理更大的群体建筑。Junfang Zhang等 [3] 研究了许多影响高层建筑和高层疏散的人为因素并设置了疏散策略。Min Fan等 [4] 提出了一种逻辑最短路径计算方法,满足了应急疏散预案设计的要求。国内对应急疏散方面的研究主要包括计算机仿真方法与数学分析法。杨雪等 [5] 提出了一种用元胞格点到出口的最短路径构建地面场的新方法,对矿工井下疏散过程进行仿真。张涛等 [6] 以某高校大型教学楼为例,基于Pathfinder软件对该教学楼建模并进行仿真模拟。朱振华等 [7] 细化了元胞自动机、改进了速度–密度公式,建立教学楼人员疏散仿真系统。傅玲等 [8] 利用元胞自动机模型对行人疏散行为的影响因素进行了模拟分析。沈文翠等 [9] 建立双路线模型和四队补齐模型,确定出安全疏散方案。武小云等 [10] 发现在有效的指挥下,人员疏散时间明显低于没有指挥的自然疏散的结论。综上,现有的研究为本文在研究方法和思路上打下了铺垫,但是同时考虑和教学楼楼梯口和楼道疏散研究相关的文献还鲜见,本文通过对华北水利水电大学具有代表性的三栋教学楼教室、楼道和楼梯出口进行实地观测,结合教学楼教室、走道、出口等实际结构和布局,研究每一层的楼层教室数、学生人数以及疏散过程中教室、楼道和楼梯出口的人员疏散情况,对教室、楼道及楼梯的情况进行建模、分析和数值仿真,研究不同的疏散路线与疏散策略情景下学生紧急疏散的效率。
2. 楼梯数据的采集、分析与建模
2.1. 研究对象
选取华北水利水电大学的三栋比较有代表性的教学楼作为研究对象,观测高峰期学生移动情况。这三栋教学楼是分别是2、3、4号教学楼,它们是本科生集中上课的场所,也比较具有代表性。2、3、4号教学楼在校园内的分布见图1,这三栋教学楼的楼间距为21米,建筑结构相同。这些教学楼共分为五层,以2号楼为例,共有32间教室,一楼和二楼有部分办公教室,三、四、五楼都为普通教室,有东西两个出口,主楼梯平台净宽3.77米,楼梯有13级踏步,副楼梯平台净宽度3.17米,两侧的副楼梯有12级踏步,主楼梯和副楼梯踏步跨度都为0.3米。
2.2. 数据的搜集与方法设计
通过对学校教学楼实地考察调研,在中午11:40~12:00下课放学期间,各楼梯出口处通常学生较多。 因此本文疏散观测时间为中午11:40~12:00,地点2号、3号和4号教学楼,以下课铃响为开始计时时间,将测量结果都换算成秒。通过实地测量和课间人群录像,得出楼梯投影面积,人群密度,人群移动时间,群集步速,各楼层持续拥堵时间以及教室使用率,下课后1~3分钟为人群出现最为拥堵的时间段,计量以及测算结果如表1所示。
Figure 1. The distribution of three school buildings (No. 2, 3 and 4)
图1. 三栋教学楼(2、3、4号)的分布图
表1. 2号教学楼楼梯口拥堵时间段数据分析表
1) 群集步速。根据拍摄下课间同学下楼视频以及实地测量等数据并结合单位面积内人群移动的时间求出人群下楼的群集步速。通过综合表1中数据可知,二、三层楼梯群集步速很小,可见人群密集,下楼速度缓慢,然后一楼和四楼次之,而相对于五楼的步速则接近于正常步速,所以,除了五楼,其它楼层都要存在不同程度的拥堵问题。
2) 人群密度。“楼梯人群密度 = 楼梯总人数/楼梯投影面积”来计算。在下楼过程中计算单层楼梯的通过人数时就可以通过测量单层楼梯面积再乘以人群密度即可。综合表1中数据可得,从五楼到一楼人群密度一直增大,一楼人群密度最大,而一楼有大厅出口,则人群密度相对二楼来说稍微变小,各层教学楼的拥堵情况可以通过人群密度变化直观显示。
3) 各楼层持续拥堵时间。根据疏散变量测算结果得出一楼至三楼出现了一段时间的拥堵,而四、五楼没有发生拥堵。相对四、五楼,下边的楼层要接受来自上边楼层的人数,人数剧增导致出现拥堵现象,并且持续相当一段时间。
2.3. 疏散变量相关性分析
对计算得出的疏散变量通过计算Pearson进行相关性分析,进一步找出在教学楼楼梯岀口疏散过程中的各疏散变量间存在的关系。总体来说,群集步速与人群密度的相关系数,以及持续拥堵时间与群集步速的相关系数均处于中等偏上水平,而人群密度与拥堵时间有较强相关性。畅通部分(人群密度小于2人/m2),各元素之间的相关性都相对较弱,尤其是群集步速和人群密度之间基本没有相关性。
拥堵部分(人群密度大于2人/m2),其中群集步速和人群密度呈−0.958高度负相关,人群密度和各楼层持续拥堵时间的相关系数为0.939,具有较高的正相关性,拥堵时间和群集步速呈−0.934高度负相关。
所以针对拥堵部分,各楼层持续拥堵时间变化趋势和人群密度变化趋势相近,二者呈正相关关系。随着人群密度的增大,各楼层持续拥堵时间增加,疏散速度降低。在相关性分析中,群集步速和人群密度的相关性较强,必须分析出群集步速和人群密度之间的关系。
3. 教室和楼道建模及数值仿真研究
3.1. 模型与方法
3.1.1. 问题描述与假设
学生在教学楼内的移动具有自主性、无序性、同时性、随机性等特征,可用元胞自动机模拟。元胞自动机通常包含元胞、移动规则、邻居、状态空间4部分 [11] 。本文对学生的紧急疏散行为用元胞自动机方法进行建模和仿真分析,仅研究在楼道内的所有学生在发现灾情后从其当前位置移动到楼道出口的疏散过程,全体学生离开教学楼则疏散完成。同时,提出下述假设:
1) 设楼道是一个长为L米,宽为W米的矩形空间,其中W < L,楼道有两个出口。基于以往众多研究结论 [12] ,可假设每个学生的平均占地面积为0.4 × 0.4 m2,随机分布在远离出口教室。
2) 将楼道矩形空间分为0.4 m × 0.4 m的矩形网格。每个网格可以为空,或者被学生占据。
3) 每个学生都同时按照地面场的指引移动,且只能移动一个网格或者不动。
4) 设学生的移动速度都相同,根据紧急情况下的学生拥挤状态,通常学生的移动速度能达到1.2 m/s,从而可知,每个时间步耗时约为0.4/1.2 = 0.33 s。
5) 为体现紧急疏散过程中学生的恐慌心理以及其它因素造成的移动迟疑,设位置保持概率为P,在每个时间步,学生以概率P保持不动,以概率1 − P发生移动。
6) 学生经过楼道出口离开楼道后不能再返回楼道内。
3.1.2. 地面场
在人员疏散问题研究中,提出了“地面场”的概念 [13] [14] [15] [16] [17] 。然而,在以往众多文献中,地面场的构建通常采用当前网格到出口的最小距离表示 [14] [15] [16] [17] 。这种构造地面场的方法对于最小距离路线上存在障碍物的情形将失效。针对上述众多文献中用距离来表示地面场在疏散空间内存在障碍物情景下的不足,在空间内存在障碍物的情境下,本文设计如下构造地面场方法:
步骤1:设教室出口所在网格(元胞)的地面场数值为0。把地面场数值为0的网格称为第1层网格。
步骤2:地面场数据中用显著大正数M表示障碍物。
步骤3:把与第1层网格相邻的、尚未设置地面场数值的网格称为第2层网格(不包含障碍物所占无据的网格)。设相邻2层网格之间地面场的势差为s,(s > 0),从而第2层所有网格的地面场数值为s。
步骤4:若第t − 1层网格的地面场数值已设置为(t − 2)s,这里正整数t ≥ 2,则把与第t − 1层网格相邻的、尚未设置地面场数值的第t层网格的地面场数值设置为(t − 1)s。
步骤5:重复步骤4,直至教室和楼道内所有网格的地面场数值设置完毕。
从而,当学生依据构造的地面场移动时,该学生所走过的轨迹实际上就是该学生从其最初位置到出口的最短路径。该方法既避免了可能穿越障碍物的错误,又能够沿着最短路径移向楼道出口。
3.1.3. 更新规则与冲突处理
在利用元胞自动机方法对学生的疏散行为模拟时,所有学生的状态应同步更新。在每一个离散的时间步,每一个学生在其所在网格的前方、左方、右方3个相邻网格中选择没有被障碍物或其他学生占用的网格,依据地面场数值越小越优先的原则,确定其向哪一个网格移动。当学生按上述规则自主移动时,若出现多个学生竞争同一网格的位置冲突,则从中等概率随机选择一名学生,允许其进入竞争网格,其他学生退回原位置。当所有学生都离开系统时,仿真结束,统计并输出结果。
3.2. 数值仿真
利用Matlab7.0编写程序对存在障碍情景下学生的紧急疏散问题进行仿真模拟。结合教学楼实地调研数据,设楼道的长度为L = 30.4 m,宽度为W = 21.2 m,把楼道分割为0.4 m × 0.4 m的网格。不妨设地面场的势差为s = 0.1,对于教室内存在桌椅等障碍物的情形,仿真中黑色区域表示墙壁等占据的空间,红色区域表示桌椅、讲台等障碍物占据的空间,484名学生在常见的五个教室内的随机分布示意图见图2。在图2 中,网格内的每个蓝色圆圈表示一名学生。
在对学生疏散过程进行数值模拟时,取位置保持概率P = 0.05,也即在每一次位置更新时,每个学生以5%的概率迟疑不动,以95%的概率按方向场指向和移动规则进行移动。按照上文所设计的学生位置更新算法和冲突处理规则,经过150步迭代后的仿真结果见图3。由图3可见,学生在疏散过程中相对有序,个别教室会出现学生疏散过程中的拥堵现象,这与实际观察到的情形基本相符。为研究学生疏散的效率,通过仿真计算,绘制疏散过程中教室和楼道内剩余学生人数n与迭代次数k 之间的变化关系曲线如图4所示。由图4可以看出,在最初的30次迭代中,曲线相对比较平缓,这表明刚开始疏散时,教室和楼道内学生人数多,相对比较拥挤,学生移动相对比较迟缓,疏散速度较慢。图4中,第30次迭代以后,曲线变的相对比较陡峭,曲线的斜率比较稳定,这表明教室与楼道内剩余的学生人数以稳定的速率减少,学生处于有序的疏散过程中。在第180次迭代以后,曲线变的更加陡峭,教室与楼道内剩余的学生人数以更快的速率减少,这表明大部分学生已经疏散出去,教室与楼道内剩余的学生已经不多,其在疏散过程中几乎不再有拥挤现象,疏散速度明显加快。在第210次迭代时,曲线与横轴相交,教室与楼道内剩余的学生人数为0,表明学生已全部疏散出去,疏散过程结束。在上述数值模拟过程中,取位置
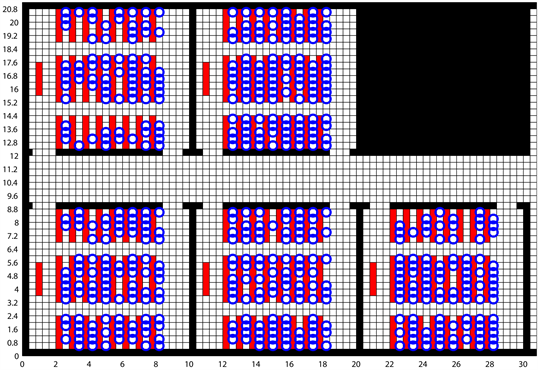
Figure 2. Atypical student’s initial position randomly distributed
图2. 一个典型的学生初始位置随机分布
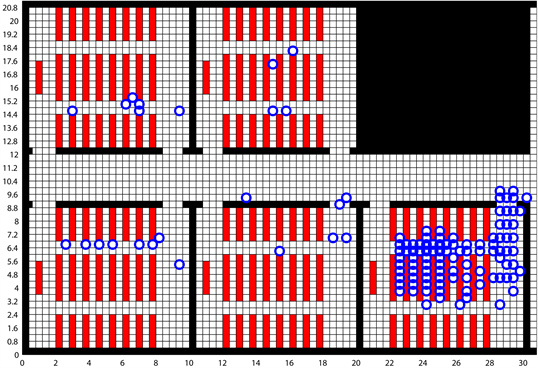
Figure 3. The simulation results after 150 iteration (p = 0.05)
图3. 经过150次迭代时的仿真结果(p = 0.05)
保持概率P = 0.05,为研究位置保持概率P变动时对学生疏散时间的影响,对于P在区间[0,0.2]上按步长0.01变化时的每个值,计算完成疏散所需要的迭代次数在20次模拟中的平均值,绘制平均迭代次数与概率P的关系曲线如图5所示。由图5可见,曲线整体上向右上方倾斜,斜率相对比较稳定,波动不大,这表明随着保持概率P的增大,学生完成疏散所需要的平均迭代次数单调增长,且增长的速率相对稳定。上述模拟结果表明,在发现灾情或接到报警信号后,为了尽快离开教室和楼道,学生应克服恐慌心理,在疏散过程中毫不迟疑地沿着最短路径向楼道出口移动,行动上的迟疑势必会增大疏散时间。仿真实验结果符合实际观察到的疏散情景。
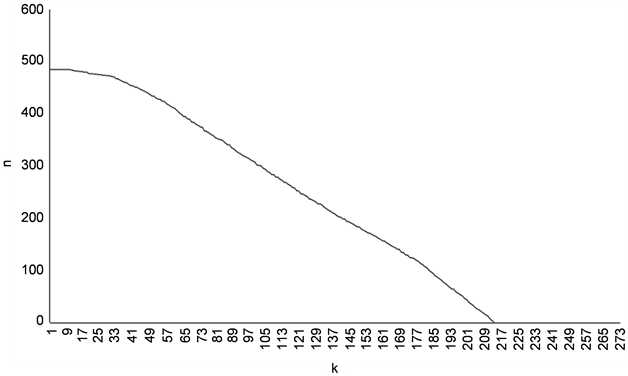
Figure 4. Evolution curve of the rest of the students (n) in corridor along with the number of iterations (k) (p = 0.05)
图4. 楼道内剩余学生人数n随迭代次数k演化曲线(p = 0.05)

Figure 5. Relation curve of the average of iteration times (K) between the probability location keeping (P)
图5. 迭代次数平均值K与位置保持概率P关系曲线
4. 结论
本文针对高校教学楼学生紧急疏散问题,对楼梯和楼道两部分进行了建模、分析及仿真研究,学生疏散过程能用建立的元胞自动机模型有效模拟。对楼梯的分析表明,教学楼楼梯出口人员疏散过程中的群集步速由人群密度决定。要缩短楼层内的持续拥堵时间,需要合理地调整人群密度来增加群集步速,提高疏散速度。结合楼梯和楼道的研究结果,在教室和楼道制定合理的应急疏散规则,降低位置保持概率,缩短楼层内的持续拥堵时间,能够使学生尽快完成疏散。
基金项目
2016年度华北水利水电大学创新创业训练计划项目。
NOTES
*通讯作者。