一类水体富营养化复杂动力系统构建及其动力学分析

Dynamics Analysis and Construction of a Water Eutrophication Complex Dynamical System

摘要: 基于吴家园水库水体富营养化研究进程，本论文在动态建模过程中引入分布式函数来刻画总磷输入随季度变化的特征，构建了一类水体富营养化复杂动力系统，对所建系统进行了一定的理论分析与数值模拟，建立了该系统内平衡点渐近稳定的判断准则，模拟出总磷浓度和藻类种群密度动态变化趋势，剖析出总磷与藻类种群之间的相互作用机制，进而揭示总磷输入可控策略对水体富营养化状况和藻类水华的影响作用机理。这些研究工作为进一步预测吴家园水库营养盐动态演化趋势和探索吴家园水库藻类种群生长动态规律提供了一定的理论基础。

Abstract: In this paper, firstly, on the basis of research progress of water eutrophication in Wujiayuan res-ervoir, a distributed function is introduced to characterize the total phosphorus input being changed with the season in the process of dynamic modeling, a water eutrophication complex dy-namical system has been structured. Secondly, some theoretical analysis and numerical simulation on the complex dynamical system have been investigated to establish some judgment criterions for the asymptotic stability of the internal equilibrium point and describe the dynamic trends of total phosphorus concentration and algal population density, which can dissect the interaction mechanism between total phosphorus and algal population, and then reveal the influence mecha-nism of total phosphorus input control strategy on eutrophication status and algal bloom. Finally, these studies can provide certain theoretical basis for the further prediction of the nutrient dy-namic evolution trend and the deep exploration of the algae population growth dynamic law in Wujiayuan reservoir.

1. 引言

目前，湖库水体富营养化及其浮游植物水华现象已是全世界共同面临的重大环境问题之一 [1] 。随着世界经济的快速发展与人口的急剧膨胀，水体富营养化引起的浮游植物水华问题更加突出，不仅导致水质恶化而丧失其功能，严重影响饮用水供水安全，还会引起水域生态系统失衡，进一步导致水体生物多样性下降 [2] 。就目前来说，亚热带湖库水体富营养化问题尤为突出，如温州吴家园水库分别在2012年10月和2014年8月发生过不同程度的藻类水华现象，导致大面积饮用水停水。因而，深入研究营养盐如何影响和驱动藻类种群生长动态变化问题变得至关重要。

湖库水体富营养化问题的主要危害是其引起的浮游植物水华使水体失去生态和使用功能，进一步导致一系列生态环境问题 [3] 。浮游植物水华爆发动态过程是在一定的营养、气候、水文条件和生态环境下藻类种群过度繁殖和聚集过程，是水体生态环境因子如TN、TP、温度、光照、pH、流速、风力、溶解氧等交互影响驱动过程 [4] 。论文 [5] 研究了光照强度、温度和营养盐如何影响滇池铜绿微囊藻生长动态变化趋势，结果揭示了滇池中总磷是限制藻类动态生长的主要因子，控制滇池水体富营养化应以控制总磷为主。论文 [6] 研究了温度、光照和磷酸盐脉冲输入对藻类生长动态演化机制的交互影响作用，解析了温度、光照和脉冲如何交互影响藻类种群生长动态机制。论文 [7] 研究了营养盐磷含量及不同温度如何动态影响铜绿微囊藻生长动态演化机制，研究结果较好地阐明了洋河水库铜绿微囊藻种群从早春到晚秋持续发生的主要原因。论文 [8] 研究了光照和磷的交互作用如何影响两种淡水藻类种群的生长动态演化趋势，研究结果表明光照和磷的交互作用严重影响铜绿微囊藻的生长动态变化机制。论文 [9] 研究了光和营养盐对浮游植物的快速生长繁殖的影响作用机制，研究结果明确了藻类种群生长比率的大小严重依赖于光和营养盐的供给情况。论文 [10] 探索了氮，磷，铁和硅等因素对5种海洋底栖硅藻生长动态的动态影响作用，剖析出氮，磷，铁和硅等因素对硅藻生长比率的影响规律。论文 [11] 研究了氮磷、温度等因素对亚热带浅水湖泊浮游植物空间组成和生物量变化趋势的影响作用，揭示了温度和总氮是影响浮游植物动态生长的关键因素。

最近几十年，国内外许多学者对湖库水体富营养化及其浮游植物水华现象做了大量研究工作，深入探析了各类因素在水体富营养化和浮游植物水华爆发动态过程中的影响驱动作用机制及其交互作用机制 [12] - [22] 。同时，随着我们对水库生态环境认识的加深，所要解决的水体富营养化问题和浮游植物水华问题日趋复杂，通过实验室试验等手段研究它们的动态演化问题能力的相对下降，在这种形势下复杂动力系统及其数值模拟技术成为了对复杂生态环境进行研究的一种重要的科学研究方法，它能够将理论分析、数据处理、实验研究和数值模拟的结果有机结合起来，并应用到具体的水库水体富营养化及其浮游植物水华现象中。最近十几年来，许多学者做了大量的研究工作 [23] - [30] ，并应用在其它各类领域，其中就包括水域生态系统。此外，各类因素对水体富营养化和浮游植物水华爆发的影响驱动机理具有非线性、随机性、突变性和积累性等特征，其中存在一些问题尚不明确，例如：如何剖析出关键影响生态环境因子对浮游植物水华爆发动态演化的影响驱动机制；如何解析各类因子在浮游植物水华爆发动态过程中的影响规律和特性等等。因此，很有必要通过建立复杂水体富营养化动态系统进行深入认识和全面解决关键生态环境因子对浮游植物水华爆发动态演化的影响驱动机理。

2. 动态建模

吴家园水库位于温州苍南县藻溪镇吴家园村，是苍南县第二大饮用水水库，年平均为60万人民群众提供清洁水源3300万立方米。但是在2014年9月9日爆发大规模藻类水华，一眼望去是绿油油的一片，被迫停止居民供水。同时，吴家园水库分别在2012年10月和2014年8月发生过不同程度的藻类水华现象。显而易见，该水库富营养化问题还是比较严峻得，严重制约了当地经济的发展与周边城镇人口饮水安全。

依据吴家园水库周边地区形势而知，吴家园水库营养盐的输入主要靠周边雨水的汇集为主，其它来源相对影响不大。同时对于淡水富营养化而说，总磷的浓度严重制约浮游植物生长动态趋势，所以预防与控制吴家园水库藻类水华爆发应以控制总磷为主。因此本论文在数学建模上给出下面的两个假设：(1) 总磷输入量是随着季度而变化的，其原因是温州苍南四个季度的下雨量有比较大的差异，根据四个季度

下雨量来估计总磷的输入量为 $I_i=\{\begin{array}{l}{I}_1,第一季度\\ I_2,第二季度\\ I_3,第三季度\\ I_4,第四季度\end{array}$ ，其中 $I_i\left(i=1,2,3,4\right)$ 代表四个季度外界输入水库总磷的

平均浓度。(2) 假设温州吴家园水库还有一部分总磷来源其它地方，可以满足浮游植物(藻类)种群生长。但是如果没有四个季度的总磷输入量的摄入，浮游植物(藻类)种群将会随着一定的时间而走向灭绝，故假设 $0<r<m$ ，其中 $r$ 代表藻类种群来自其它来源总磷的平均增长率， $m$ 代表藻类种群平均死亡率。

基于上面的两个假设框架和营养盐与藻类种群之间的相互作用机制，本论文将建立一类基于吴家园水库的水体富营养化复杂动力系统，其数学模型可以表述如下：

$\{\begin{array}{l}\frac{\text{d}x\left(t\right)}{\text{d}t}=I_i-bx\left(t\right)-\frac{ax\left(t\right)y\left(t\right)}{c+x\left(t\right)}\\ \frac{\text{d}y\left(t\right)}{\text{d}t}=ry\left(t\right)+\frac{aex\left(t\right)y\left(t\right)}{c+x\left(t\right)}-my\left(t\right)\end{array}$ (1)

其中 $x\left(t\right),y\left(t\right)$ 分别代表在时间 $t$ 时刻总磷的浓度(mg/L)和藻类种群的密度(10⁸个/L)， $b$ 代表总磷的流失率， $a$ 代表藻类种群对总磷的吸收率， $c$ 表示半饱和常数， $e$ 表示磷营养转化为藻类种群生长能量的转化率，所有参数取值都为正值。

在富营养化动态建模过程中，我们引入了一个季度分段式函数来表示总磷的输入量，进而刻画出吴家园水库总磷的实际流入情况与特点，并假设藻类种群生长严重依赖营养盐–总磷的限制，因而以此为基础，本论文主要探析总磷输入量怎样影响藻类种群生长动态变化趋势。

3. 理论分析

为了剖析出总磷营养盐如何影响藻类种群生长动态变化趋势，将对所建富营养化复杂动力系统(1)进行相关动力学性质分析。就目前来说，亚热带水库藻类水华控制的实质问题就是尽可能地维持水库水域浮游植物(藻类)群落的浓度远低于藻类水华爆发数量级，但是要求浮游植物浓度等于零这是不可能实现。然而借助生态数学模型可以理论上获得一些参数限制条件，保证藻类种群的数量级远低于藻类水华爆发的数量级阈值。因此，本论文主要讨论富营养化复杂动力系统(1)的内平衡点的存在性就可以，同时，能够保证藻类种群的生长数量级远低于藻类水华爆发数量级，那就说明不会诱发藻类水华的爆发。

定理3.1：富营养化复杂动力系统(1)存在内平衡点 $E\left(x_1,y_1\right)$ 当且仅当 $m-r<\frac{I_{i}ae}{bc+I_i}$ ，其中 $x_1=\frac{\left(m-r\right)c}{ae+r-m}$ ， $y_1=\frac{e\left[I_i\left(ae+r-m\right)-bc\left(m-r\right)\right]}{\left(ae+r-m\right)\left(m-r\right)}$ 。

证明：由富营养化复杂动力系统(1)可知，内平衡点满足方程组(2)

$\{\begin{array}{l}{I}_i-bx\left(t\right)-\frac{ax\left(t\right)y\left(t\right)}{c+x\left(t\right)}=0\\ r+\frac{aex\left(t\right)}{c+x\left(t\right)}-m=0\end{array}$ (2)

进而解得 $x_1=\frac{\left(m-r\right)c}{ae+r-m}$ ， $y_1=\frac{e\left[I_i\left(ae+r-m\right)-bc\left(m-r\right)\right]}{\left(ae+r-m\right)\left(m-r\right)}$ 。由动态建模研究意义，可知 $x_1>0$ ， $y_1>0$ ，因而，可以求得 $\{\begin{array}{l}m-r<\frac{I_{i}ae}{bc+I_i}\\ \left(m-r\right)\left(ae+r-m\right)>0\end{array}$ 。根据建模假设框架可知，只需要参数满足 $m-r<\frac{I_{i}ae}{bc+I_i}$ 即可。

在富营养化复杂动力系统(1)内平衡点存在的基础之上，现在推导出相关稳定性结果，并给出一些关键参数所限制的阈值表达式，这些理论条件是进一步数值模拟分析的判断准则。

定理3.2：如果条件 ${\left(b+\frac{\left(ae+r-m\right)H_1}{aec\left(m-r\right)}\right)}^2>\frac{4\left(ae+r-m\right)H_1}{aec}$ 是成立得，其中 $H_1=I_i\left(ae+r-m\right)-bc\left(m-r\right)>0$ ，那么平衡点 $E\left(x_1,y_1\right)$ 是局部渐近稳定的。

证明：为了研究平衡点 $E\left(x_1,y_1\right)$ 的稳定性，设富营养化动力系统(1)的扰动解为 $\left(x\left(t\right),y\left(t\right)\right)$ ，作变换

$u\left(t\right)=x\left(t\right)-x_1,v\left(t\right)=y\left(t\right)-y_1$ (3)

把变换(3)代入系统(1)，再进行线性近似，其线性化近似的微分方程为

$\{\begin{array}{l}\frac{\text{d}u\left(t\right)}{\text{d}t}=a_{11}u\left(t\right)+a_{12}v\left(t\right)\\ \frac{\text{d}v\left(t\right)}{\text{d}t}=a_{21}u\left(t\right)+a_{22}v\left(t\right)\end{array}$ (4)

其中

$a_{11}=-b-\frac{I_i{\left(ae+r-m\right)}^2-bc\left(m-r\right)\left(ae+r-m\right)}{aec\left(m-r\right)}$ , $a_{12}=\frac{r-m}{e}$

$a_{21}=\frac{I_i{\left(ae+r-m\right)}^2-bc\left(ae+r-m\right)\left(m-r\right)}{ac\left(m-r\right)}$ , $a_{22}=0$

因此特征方程为 ${\lambda }^2-a_{11}\lambda -a_{12}{a}_{21}=0$ 。

如果 $a_{11}^2>-4a_{12}{a}_{21}>0,a_{11}<0$ ，那么特征方程有且只有两个负根。

基于Routh-Hurwitz准则，平衡点 $E\left(x_1,y_1\right)$ 就是局部渐近稳定的，即只要 ${\left(b+\frac{H_1}{m-r}\right)}^2>4H_1$ 成立，其中 $H_1=\frac{I_i{\left(ae+r-m\right)}^2-bc\left(m-r\right)\left(ae+r-m\right)}{aec}>0$ ，那么平衡点 $E\left(x_1,y_1\right)$ 是局部渐近稳定的。

基于水体富营养化复杂动力系统(1)的构建假设，知道由于总磷的输入量是随着四个季度变化而变的分段函数，所以复杂动力系统(1)包含了四个子系统，而且每个子系统都具有一个内平衡点，分别为 $E_1\left(x_{11},y_{11}\right)$ ， $E_2\left(x_{12},y_{12}\right)$ ， $E_3\left(x_{13},y_{13}\right)$ ， $E_4\left(x_{14},y_{14}\right)$ 。定理1是要求四个子系统内平衡点都存在的阈值条件，定理2是要求四个内平衡点都是渐近稳定的阈值条件。但是由于吴家园水库藻类大量繁殖时期是在一段时间内，所以本论文只要求在藻类大量繁殖期满足内平衡点存在就可以，同时不要求所有内平衡点都是稳定的，只有一些平衡点是稳定的，其它平衡点不是稳定的。

4. 数值模拟与分析

为了深入剖析出总磷的输入量如何影响藻类种群生长动态变化趋势和全面解析吴家园水库总磷与藻类种群相互作用机制，依据前面理论分析结果，对水体富营养化复杂动力系统(1)的相关动力学行为进行数值模拟与分析。根据澳大利亚和新西兰环保委员会和农业资源管理委员会发布的《Australian and New Zealand Guidelines for Fresh and Marine Water Quality》，当藻类密度数超过1500万个/L时，就建议不要接触皮肤。同时参考《地表水环境质量标准》(GB3838-2002)中的分级方法，藻类密度数200万个/L作为3级标准限值，1500万个/L作为4级标准限值，藻类密度数10,000万个/L作为5级标准限值，也可以作为藻类水华爆发的判断依据。此外，一般认为总磷浓度达到0.05 mg/L作为水体达到营养化状态。因此，我们假设系统(1)的总磷的浓度为0.055 mg/L，即意味着水体已经到达富营养化程度，藻类种群的密度为1000万个/L，即藻类种群在快速生长初期。进一步，依据其它参数的生物学意思及其吴家园实际监测数据，其它参数取值为 $a=0.5,e=0.6,c=1.25,b=0.25$ 。

为了揭示理论结果的可行性和关键参数取值范围的率定性，图1分别描述了关键参数取值动态变化趋势。理论计算出总磷输入量 $I_i>\frac{0.3125\left(m-r\right)}{0.3+r-m}$ 时，可保证系统(1)的四个内平衡点是存在的。图1(a)动态描述了关键参数 $I_i,r,m$ 之间的相互制约关系，显然在 $r\in \left[0.02,0.2\right]$ 和 $m\in \left[0.02,0.2\right]$ ，总磷输入量 $I_i$ 具

有可取值域。图1(b)揭示了关键参数 $I_i,m$ 之间的相互制约关系( $r=0.18$ )，说明随着藻类种群死亡率取值的增加，总磷输入量是一个增加的趋势，也就说明它们具有正相关性。如果取定 $m=0.19$ ，也就是现在吴家园水库放养了大量滤食性鱼类去捕食藻类种群，则 $I_i>0.01077586207$ 时可以维持系统(1)具有四个内平衡点。依据监测数据与实验室模拟数据，首先对富营养化复杂动力系统(1)进行生境动态数值模拟，假设四个季度的总磷输入分别为0.005 mg/L，0.015 mg/L，0.02 mg/L和0.005 mg/L，显然系统(1)仅有两个子系统存在正平衡点，生境动态变化趋势被描述在图2中(1t代表24小时)。很容易发现：在三年时间里，

总磷的浓度在每年的4月~9月内是大于0.055 mg/L，也就是说在模拟生镜中，这段时间内水质处于富营养化状态中。同时，在每年的7月~9月内，藻类种群的密度快速增加，可以形成轻微的水华现象。总而言之，当四个季度的总磷输入分别为0.005 mg/L，0.015 mg/L，0.02 mg/L和0.005 mg/L时，数值模拟系统(1)的实际运行生态环境是处于水体富营养化状态下，且藻类种群快速繁殖，已可以在定期内形成轻微藻类水华现象。

为了治理吴家园水库水体富营养化状况和控制藻类水华现发生，现在主要实施两个方案，一是放养鳙鱼和鲢鱼，控制藻类种群，二是水库周边实施点源控制营养盐的输入。本论文主要揭示点源控制营养盐的输入能否降低总磷的含量和控制藻类水华现象。假设吴家园水库周边已经实施点源控制策略，降低四个季度的总磷输入量分别为0.0035 mg/L，0.011 mg/L，0.012 mg/L和0.0035 mg/L，显然系统(1)也是有两个子系统存在正平衡点，生境环境动态变化趋势被描述在图3中(1t代表24小时)。很容易发现：总磷的浓度在三年内是低于0.05 mg/L，也就是说，系统水质环境总体上保持非富营养化状态，同时藻类种群在第一年内是逐步降低的，并趋于灭绝状态。显然这个数值模拟结果与现实结果有点不符合，但是，此研究结果可以说明实施点源控制总磷的输入可以降低水体中总磷的含量，同时控制藻类水华现象的爆发。所以，本研究结果和吴家园水库治理理论结果基本符合，但是不管如何，这个结果说明了此类系统可以基本反映吴家园水库水体富营养化治理理论策略。

5. 结论

基于亚热带水库水域富营养化状况与吴家园水库水质监测情况，在动态建模过程中引入总磷输入分

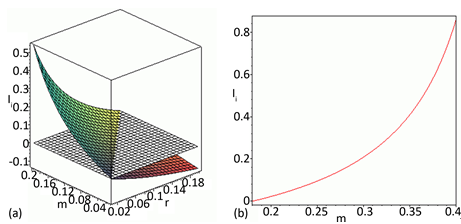
Figure 1. The value distribution trend of key parameters

图1. 关键参数取值分布趋势

Figure 2. The simulated dynamic evolution trend of total phosphorus concentration and algal population density of the system (1)

图2. 系统(1)中总磷浓度与藻类种群密度的模拟动态演化趋势

Figure 3. The simulated dynamic evolution trend of total phosphorus concentration and algal population density of the system (1) under the condition of controlled total phosphorus

图3. 实施可控总磷条件下系统(1)中总磷浓度与藻类种群密度的模拟动态演化趋势

布式函数，建立了一类水体富营养化复杂动力系统，对所建复杂动力系统进行定性分析与数值模拟，研究了该系统内平衡点的存在性与稳定性，明确了所推结果的可行性，并进一步数值模拟出总磷浓度与藻类种群密度动态变化趋势，解析总磷浓度和藻类种群密度动态演化特性，揭示吴家园水库总磷可控策略的有效性。这些研究工作为进一步预测吴家园水库总磷动态演化趋势和探索吴家园水库优势藻类种群生长动态规律提供了一定的理论基础。

致谢

感谢浙江省水环境与海洋资源重点实验室的同仁们，感谢你们一直以来在实验室对我们问题的细致引导、鼓励和解答，使我们对专业有了更深更细致的理解。

基金项目

国家自然科学基金面上项目(31570364)，浙江省公益技术研究项目基金项目(2015C33227, 2015C33246)，浙江省自然科学基金项目(LY14C030006, LY16BO70008)，温州科技计划项目(S20140028和S20140024)的资助。