1. 引言
微电网作为分布式发电单元接入电网的一种有效手段,逐渐引起了广泛关注 [1] ,在高渗透率下多微电网配电网管理系统中,微电网主要包括:分布式发电(Distributed Generation)类型的微型发电设备(例如微型燃气轮机、燃料电池、风机、光伏阵列)、储能设备(例如飞轮、储能电容和电池)和可控(柔性)负荷设备(例如电动汽车),这些具有可控能力的设备允许连接到上级高压配电网并网运行,当大电网出现故障或其他外部扰动或自然灾害时可以脱离主网实现孤岛独立运行,从而提高供电质量 [2] [3] [4] 。
为有效抑制环流及改善系统无功的均分问题,本文对传统下垂控制的功率分配进行分析,引入感性虚拟阻抗的多逆变器的控制策略,由滤波电阻值决定其输出阻抗,进而决定其功率输出;通过考虑线路阻抗对传统下垂控制算法的影响,得到电阻与下垂系数的关系,提出一种改进型下垂控制算法。通过实验仿真验证了所提方法的有效性。
2. 传统下垂控制方法分析
以3台逆变器并联为例,图1为使用3个电压源逆变器的3个分布式电源微电网结构图,其中L、C分别为逆变器的输出起滤波作用的滤波电感和滤波电容,R1为分布式直流电源1的等效逆变器输出电阻和线路电阻之和,X1为分布式电源1的等效逆变器输出电抗和线路电抗之和;R2为分布式电源2的等效逆变器输出电阻和线路电阻之和,X2为分布式电源2的等效逆变器输出电抗和线路电抗之和;R3为分布式电源3的等效逆变器输出电阻和线路电阻之和,X3为分布式直流电源1的等效逆变器输出电抗和线路电抗之和,K为逆变器的输出继电器。
U1∠θ1、U2∠θ2和U3∠θ3分别为分布式电源逆变器的空载输出电压;θ1、θ2、θ3为分布式电源逆变器的空载输出电压与母线电压的相角差。由图2可得逆变器i (i = 1, 2, 3)输出的有功功率和无功功率分别为
(1)
(2)
式中第i个逆变器的阻抗幅值为
:
(3)
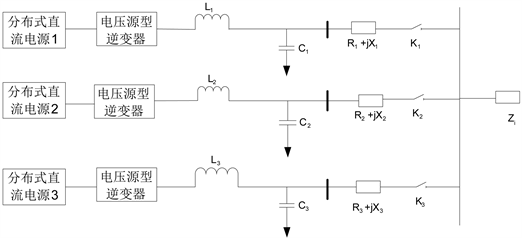
Figure 1. A microgrid structure with 3 distributed sources
图1. 含有3个分布式电源的微电网结构图
式中
包含第i个逆变器的输出阻抗和线路阻抗;
为第i个逆变器的输出电阻和线路电阻之和;
为第i个逆变器的输出感抗和线路感抗之和;
为第i个逆变器的空载输出电压幅值;
为第i个逆变器的空载输出电压与母线的相角差;
为阻抗角,
(4)
在高压系统中,传统下垂控制策略应用于系统等效输出阻抗为感性的系统,即满足
,此时可忽略逆变器的输出电阻和线路电阻之和
,简化得到
(5)
(6)
实际中相角
很小,可近似得到
,
,式(5)和(6)可分别简化
(7)
(8)
由上式可知,逆变器输出的有功功率主要受逆变器的空载输出电压与母线的相角差影响,逆变器输出的无功功率主要受逆变器的空载输出电压幅值影响,由于实际工程中逆变器的空载输出电压与母线的相角差很难检测到,因此一般由频率代替相角实现控制,可得P/f下垂控制方程表达式 [14] :
(9)
式中—
、
分别为逆变器输出频率、电压;
、
分别为逆变器的额定频率、额定电压;
、
分别为逆变器的有功/频率(P/f)、无功/电压(Q/U)下垂控制系数;
、
分别为逆变器的有功功率和无功功率;
、
分别为逆变器的额定有功功率、额定无功功率。
而在实际的低压微电网中,线路阻抗主要成阻性 [15] ,即满足
,此时可忽略逆变器的输出感抗和线路感抗之和
,简化可得
(10)
(11)
实际中相角
很小,可近似得到
,
,可得以下表达式
(12)
(13)
由上式可知,逆变器输出的有功功率主要受逆变器的空载输出电压幅值影响,逆变器输出的无功功率主要受逆变器的空载输出电压与母线的相角差影响,由于实际工程中逆变器的空载输出电压与母线的相角差很难检测到,因此一般由频率代替相角实现控制,可得到P/V下垂控制
(14)
式中u,v为下垂控制系数。由以上高、低压线路阻抗的特性分析可知,逆变器输出的有功、无功功率偏离额定有功、无功功率时,电压与频率值较额定值也有一定量的偏移,因此上述P/f与P/V下垂控制均为有差调节。
2.1. 传统下垂控制的功率分配
2.1.1. 无功功率分配
本文分析传统下垂控制的功率分配是基于阻性线路。
(15)
根据上式,当3台逆变器的频率相等(
)系统达到稳定时,只需使下垂系数与其额定功率成反比,即满足
(16)
(17)
即可使逆变器的无功率按期额定功率平均分配,即满足
(18)
当无功功率在实现均分时,则
(19)
若
,
,则有下式成立
(20)
2.1.2. 有功功率分配
(21)
由上式可知,要保证有功功率的平均分配,应满足下式
(22)
(23)
而使下式
(24)
成立的条件是
(25)
在上式成立时,逆变器之间的电压差为
(26)
将下式的无功/电压下垂方程代入其有功表达式(21)得
(27)
将上式代入公式(26)得
(29)
由以上公式可知,当下式成立时,即
(30)
逆变器的无功功率将按额定容量平均分配。
综上可知,基于传统下垂控制的逆变器的有功与无功功率均分的条件应满足下式
(31)
(32)
3. 逆变器的控制策略及输出阻抗设计
3.1. 虚拟阻抗法
实现逆变器输出功率均分及抑制系统环流,均是通过虚拟阻抗对分布式发电单元之间的差异调节控制,在逆变器的输出端引入虚拟阻抗的实质是在电压闭环中加入一个输出阻抗调节模块的负反馈,将虚拟阻抗值与采集的电流乘积引入到电压调节中。虚拟阻抗的引入,不仅可以改变逆变器的功率传输特性,还可以解决线路阻抗引起的功率耦合,引入虚拟阻抗的3台逆变器并联运行等效图如图3。
如图3所示,
为逆变器虚拟阻抗; 为逆变器输出电压;
为逆变器输出电压; 为逆变器输出的虚拟电压。其关系如下公式
为逆变器输出的虚拟电压。其关系如下公式
(33)
通过对逆变器的虚拟阻抗值
的调节控制虚拟电压,进而实现间接对逆变器的输出电压控制,达到对分布式发电单元逆变器输出功率均分及抑制系统环流的目的。
3.2. 虚拟阻抗的电容电流反馈控制逆变器结构分析
本文对并联逆变器采用带虚拟电感的电容电流反馈的双闭环控制相结合的方法,外环采用PI控制的电容电压控制环,用以提高系统输出功率的精度,内环采用P控制的电感电流控制环,用以改善系统的
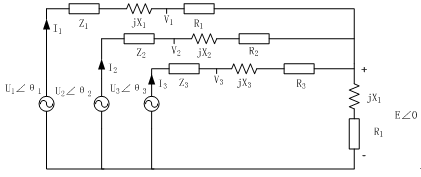
Figure 3. Parallel operation equivalent diagram of 3 inverters with virtual impedance introduced
图3. 引入虚拟阻抗的 3台逆变器并联运行等效图
动态性能。带虚拟阻抗的电容电流反馈控制逆变器结构图如图4。
引入虚拟电感后的电压参考值
;电压外环参考电压
,
,
分别为PI控制器的比例和积分系数;
为电流内环参考电流,
为电流环调节器比例系数;
为数字控制延时;
为逆变器增益;L、C分别为主电路滤波电感、滤波电容;
、
分别为电感电流、电容电压反馈系数;
为逆变器输出电压;
为线路电流;
为虚拟阻抗。由图4可知,当未加入虚拟电感时:
(34)
(35)
(36)
由于滤波电容C的值较小可忽略不计,上式可近似为
(37)
因此公式(35)可以等效为
(38)
由上式可得逆变器的输出阻抗
(39)
引入虚拟阻抗
,可得
(40)
加入虚拟阻抗
的逆变器等效输出阻抗为
(41)
将公式(39)代入(41)若使
,可得
。
综上,工频条件下引入虚拟阻抗
,输出电阻可忽略,输出阻抗近似为纯感性,即逆变

Figure 4. Capacitor current feedback control structure of inverter with virtual impedance
图4. 带虚拟阻抗的电容电流反馈控制逆变器结构图
器的输出阻抗值由滤波电感值确定,因此在对传统下垂控制方法改进时,即可利用图4控制策略对3台并联运行的逆变器进行控制,可不考虑各并联逆变器的输出电阻,仅需考虑滤波电感值。
4. 传统下垂控制算法的改进
由图4引入虚拟阻抗的控制策略,式中
为第i个逆变器的输出电阻和线路电阻之和;
为第i个逆变器的输出感抗和线路感抗之和,有上述分析可知,为了降低
对并联系统的环流的影响,对传统下垂控制算法进行改进的算法如下
(42)
式中
、
为下垂系数,当
时,此时
虽然相对较小,但是仍然存在,系统能否并联成功,
、
这两参数至关重要。
、
可提高功率均分精度,减小系统环流。首先应考虑下垂系数
、
,再根据有功、无功公式并考虑
确定
、
,从而对传统下垂控制算法进行改进。
考虑到
、
对功率均分的影响,可得
(43)
(44)
上式中
、
为逆变器输出电压最大频率偏差和幅值偏差,
、
为输出最大有功、无功功率值。
对以下公式中的
、
求导
(45)
可得
(46)
(47)
有上式(46)、(47)可得
、
的关系
(48)
上式(48)化简得:
(49)
由于并联逆变器在运行时空载输出电压与母线电压的相角差
很小,阻抗角
远大于相角差
,
上式可化简为
(50)
对以下公式中的
、
求导
(51)
可得
(52)
(53)
有上(52)、(53)式可得
、
的关系
(54)
上式(54)化简得
(55)
由于阻抗角
远大于相角差
,上式(55)可化简为
(56)
综上,多逆变器并联的微电网改进型下垂控制算法如下
(57)
当
时,上式即为传统下垂控制算法,若引入感性虚拟阻抗,参考电压
则为
(58)
5. 实验仿真验证
为了验证多逆变器并联的微电网改进型下垂控制算法,本文在Matlab/Simulink仿真平台搭建了3台逆变器并联运行仿真模型。微网电压等级380 V、单台逆变器功率等级50 kW、负载类型为阻感性负载,3台逆变器线路阻抗均为0.1 + j0.03Ω,仿真参数如表1。3台并联逆变器模型基本结构如图5。

Table 1. Simulation parameters of three inverters in parallel operation
表1. 三台逆变器并联运行仿真参数
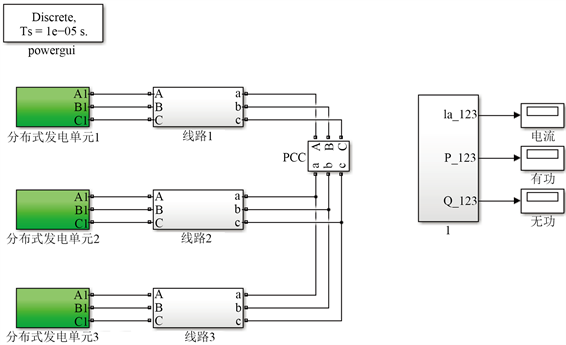
Figure 5. Basic structure of 3 parallel inverters models
图5. 3台并联逆变器模型基本结构
以下为未加入感性虚拟阻抗的传统下垂控制算法时的实验仿真波形如图6,加入感性虚拟阻抗的改进下垂控制算法的实验仿真波形如图7,仿真时间为16秒。
在3台逆变器并联运行工况下,第8秒,分布式发电单元1线路的继电器闭合,本地负载增加,由3台分布式发电单元并联运行的仿真波形变化情况分析可知,图6(a)和图6(a)为3台逆变器并联运行时的稳态电流仿真波形图,电流幅值在第8秒开始变大,后趋于稳定,但是电流幅值整体并不均匀(即出现环流,稍后详解),而加入感性虚拟阻抗后的稳态电流幅值更均匀。图6(b)和图7(b)为3台逆变器并联运行时的输出有功仿真波形图,有功在第8秒变大,后趋于稳定,未加入感性虚拟阻抗与加入感性虚拟阻抗后的输出有功仿真波形图基本保持一致,不论负载如何变化,系统有功始终维持不变。图6(c)和图7(c)为3台逆变器并联运行时的输出无功仿真波形图,未加入感性虚拟阻抗时本地负载增加前后,逆变器并联运行时输出无功均衡效果较差,加入感性虚拟阻抗后,逆变器并联运行时输出无功均衡效果较之前有很大的提高。
由于任两台逆变器之间的环流即为
,i1和i2为任意两台逆变器连接线路上的电流,可知
的幅值越大,表明实际的环流越大。图8(a)和图9(a)分别为3台逆变器线路连线上的电流仿真波形。
通过对图8(a)和图9(a)稳态电流仿真波形图对比分析,可知改进下垂控制算法的3台逆变器稳态输出电流的幅值、相位基本一致,即改进下垂控制算法的环流较小。对比图8(b)和图9(b)输出有功仿真结果,可知传统下垂控制算法的3台逆变器并联运行时输出有功在0.01秒至0.04秒之间出现不一致,之后趋于稳定,而改进下垂控制算法输出有功始终保持一致,即输出有功均衡效果较好。对比图8(c)和图9(c)
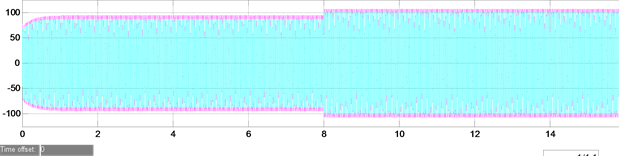 (a)
(a) 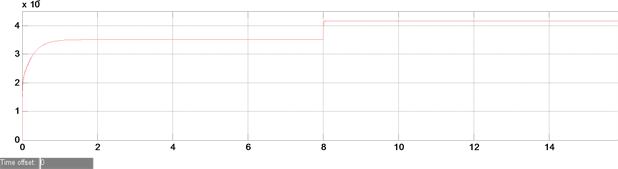 (b)
(b)  (c)
(c)
Figure 6. Experimental simulation waveforms of traditional droop control algorithm without inductive virtual impedance. (a) Steady state current simulation results of 3 inverters in parallel operation; (b) Simulation results of output active power in parallel operation of 3 Inverters; (c) Simulation results of reactive power output in parallel operation of 3 inverters
图6. 未加入感性虚拟阻抗的传统下垂控制算法时的实验仿真波形。(a) 3台逆变器并联运行时的稳态电流仿真结果;(b) 3台逆变器并联运行时输出有功仿真结果;(c) 3台逆变器并联运行时输出无功仿真结果
 (a)
(a)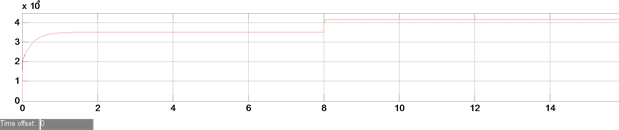 (b)
(b) (c)
(c)
Figure 7. Experimental waveforms of improved droop control algorithm with inductive virtual impedance. (a) Steady state current simulation results of 3 inverters in parallel operation; (b) Simulation results of output active power in parallel operation of 3 inverters; (c) Simulation results of reactive power output in parallel operation of 3 inverters
图7. 加入感性虚拟阻抗的改进下垂控制算法的实验仿真波形。(a) 3台逆变器并联运行时的稳态电流仿真结果;(b) 3台逆变器并联运行时输出有功仿真结果;(c) 3台逆变器并联运行时输出无功仿真结果
 (a)
(a) 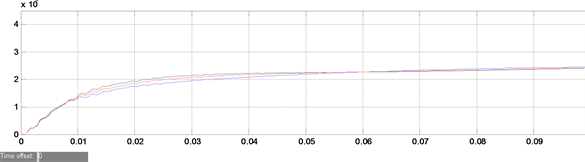 (b)
(b) (c)
(c)
Figure 8. The simulation waveform of traditional droop control algorithm is as follows. (a) Steady state current simulation results of 3 inverters in parallel operation; (b) Simulation results of output active power in parallel operation of 3 inverters; (c) Simulation results of reactive power output in parallel operation of 3 inverters
图8. 传统下垂控制算法时的实验仿真波形如图。(a) 3台逆变器并联运行时的稳态电流仿真结果;(b) 3台逆变器并联运行时输出有功仿真结果;(c) 3台逆变器并联运行时输出无功仿真结果
 (a)
(a) 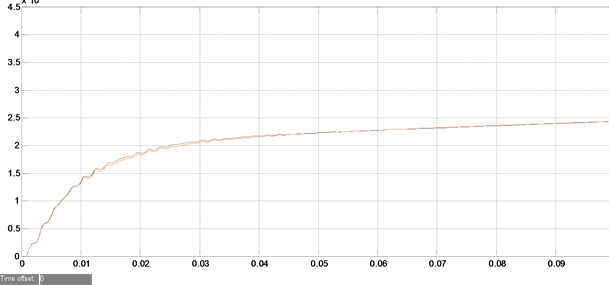 (b)
(b)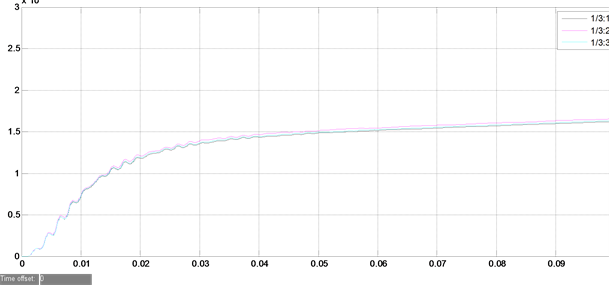 (c)
(c)
Figure 9. Experimental simulation waveform chart of improved droop control algorithm. (a) Steady state current simulation results of 3 inverters in parallel operation; (b) Simulation results of output active power in parallel operation of 3 inverters; (c) Simulation results of reactive power output in parallel operation of 3 inverters
图9. 改进下垂控制算法的实验仿真波形图。(a) 3台逆变器并联运行时的稳态电流仿真结果;(b) 3台逆变器并联运行时输出有功仿真结果;(c) 3台逆变器并联运行时输出无功仿真结果
输出无功仿真结果,传统下垂控制算法的3台逆变器并联运行时输出无功在0.005秒后出现较大的波动,即无功均衡效果较差,而改进下垂控制算法输出无功基本保持一致,无功均衡效果较好。
6. 结论
由于实际的微电网的逆变器输出阻抗不同;其到公共并网点的距离长短不一,实现阻感性或者纯阻性线路不同容量逆变器有功、无功功率的均分时各逆变器的电压幅值和相位不一致;容量与线路阻抗成反比,采用传统下垂控制策略,很难实现逆变器的功率均分。
本文通过对传统下垂控制算法的有功、无功分析,设计了引入虚拟阻抗的电压电流双环控制策略;提出一种改进型多逆变器并联的微电网改进型下垂控制算法。实验仿真结果表明,改进型多逆变器并联的微电网改进型下垂控制算法提高了多逆变器的并联性能,有效减小了多逆变器并联运行环流问题,大大提高了多逆变器并联运行的无功均衡效果。
基金项目
自治区重点实验室项目(2015kl020, 2016D03021);国家863计划项目(2013AA050604);教育部创新团队项目(IRT1285)。