1. 引言
2013年6月,在利率市场化的背景下,余额宝正式上线,这是第三方支付平台支付宝与天弘基金合作推出的兼具理财和消费支付功能的互联网理财产品,也是我国第一支互联网货币基金。此后半年内其迅猛发展,成为国内首支规模破千亿的基金。截止2017年3月31日,余额宝资产规模达到11,396.38亿元,比上期增长40.99%。相比于传统的货币基金,余额宝取消了最低门槛限制,简化了开户流程,増加了随时消费支付,收益即时分配到账等功能。不仅实现了技术创新和渠道创新,并且提高了对碎片化资金的利用效率。在强大的示范效应下,基金公司、互联网平台纷纷推出各种“宝宝”类理财产品加入混战。然而目前对于互联网货币基金收益率波动性及收益率预测的研究还较为缺乏,金融资产的风险一般表现为收益的不确定性,在对互联网货币基金收益率的预测的基础上,可以对互联网货币基金的风险特征进行更多的分析,促进基金的稳定发展,提高投资者的风险意识,保护投资者的利益。因此,对于互联网货币基金收益率的预测具有重要的现实意义。
时间序列模型在对传统金融时间序列的拟合预测上有着不可无视的优势,但由于互联网货币基金独有的风险特点,使用原始的时间序列方法拟合互联网货币基金的收益率序列的结果往往差强人意,时间序列模型不能准确地描述互联网货币基金的收益率波动,对于收益率的极端值也更加难以捕捉,用时间序列模型估计互联网货币基金收益率的未来走势效果并不显著。与传统理论相比,以非线性假设为前提的人工神经网络模型拥有明显的非线性映射的特点。它可以实现对数据的分布式存储且学习能力强。运用神经网络模型使得在预测准确度上有所提升。因此,该模型在金融领域受到广大学者的青睐。而组合模型可以集合传统时间序列模型和非线性的神经网络模型的优势,进一步提高对互联网货币基金收益率预测的准确度。因而引入人工神经网络方法,在BP神经网络模型基础上建立与传统的广义自回归条件异方差模型结合的组合预测模型对互联网货币基金收益率序列进行拟合与预测。
作为隐形的基金模式,互联网货币基金表现出强劲生命力的同时也包含着阻碍自身和国民经济健康发展的潜在风险。周正清(2014)对T + 0型货币基金快速发展背后存在的流动性管理能力不足、估值方法未能充分反映风险等问题进行深入分析,并结合欧美主要国家有关货币基金的管理经验及国际金融危机后的监管改革动向,提出完善我国T + 0型货币基金管理的相关建议 [1] 。赵舒怡、李敬湘(2015)以余额宝为出发点对互联网货币基金的发展优势和潜在风险进行了探讨,并分别在政府、金融企业以及基金购买角度提出相关建议,以保证互联网货币基金得到健康发展以及消费者权益得到保护 [2] 。然而对于互联网货币基金收益率数据的预测分析较少。
1986年,Rumelhart和Meclland提出了误差反向传播算法(BP算法)。随着研究的逐渐深入,多种人工神经网络模型被提出并得以深入研究,但BP神经网络及它的改进形式约占现有神经网络模型的80%~90%。BP神经网络具有结构简单,可操作性强、较好的自学习和自适应能力、能模拟任意的非线性输入和输出关系等优点。目前神经网络已被广泛用于模式识别、智能控制、预测、图像识别、函数拟合、系统仿真等领域。对于经济预测方面,Matsuba (1991)率先将神经网络应用到估值预测中 [3] 。其后,Liu,Yao (2001)运用基于进化算法的前馈神经网络对香港恒生指数进行了预测,取得了良好的结果 [4] 。而刘澄等(2009)利用基于遗传算法的BP神经网络模型拟合股指波动趋势,并选取上证指数为样本进行实证分析 [5] 。Wang Guo (2011)建立以小波变换为基础的BP神经网络模型来预测股票价格波动,对上证综合指数的月度数据展开分析,经过实证对比发现,经小波变换法优化处理的BP神经网络模型输出相对较优 [6] 。
组合预测模型的思想最初由Bates和Granger在1969年提出,即将参与组合的不同预测模型按一定权重进行组合,发挥不同模型的优势,以期提高模型的预测精度 [7] 。组合模型的提出得到了各国学者的高度重视,经过不断深入的研究,以及对数据挖掘和人工智能理论的参考,在组合模型中引入了遗传算法、粒子群算法及人工鱼群等智能算法,使得组合预测模型在模型选择、权重确定等方面得到了很大发展。Roselina (2008)将ANN模型、ARIMA模型及其混合模型作比较,发现混合模型的预测精度要比单一模型的预测精度要高 [8] 。张东等(2013)将改进的指数平滑模型与BP神经网络模型进行组合,并应用于上证收盘指数的预测,经实证分析,组合模型预测结果优于单个模型的预测结果 [9] 。
2. 模型介绍
2.1. BP神经网络模型
BP神经网络是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。它的学习规则是使用最速下降法,通过反向传播来调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络由输入层、隐藏层、输出层三层构成 [10] 。
设输入层有
个神经元,输入信息为
,期望输出为
,实际输出为
,则,隐层输出值为
(1)
输出误差为
(2)
其中,
为激活函数,
为阈值。
隐层权值调整公式为
(3)
为学习速率,
为误差信号。
2.2. GARCH模型
自回归条件异方差模型(ARCH模型)的基本思想指在以前信息集下,某一时刻一个噪声的发生服从正态分布。该正态分布均值为零,方差随时间变化,即为条件异方差 [11] 。且这个随时间变化的方差为过去有限项噪声值平方的线性回归,即为自回归。因而构成了自回归条件异方差模型。根据Engle提出的定义,ARCH(p)模型表达式如下
(4)
其中,
和
分别表示因变量、自变量,
表示无序列相关的随机扰动项,
表示条件方差。公式中第一个等式称为均值方程,第二个等式称为方差方程。
为了解决ARCH模型通常需要较大的阶数才能有较好的拟合结果,这样就需要估计更多的参数,为解决这一问题计量经济学家Clive Granger提出了广义自回归条件异方差模型(GARCH模型),GARCH模型允许条件方差依赖自身的前期,简化了ARCH模型。GARCH(p,q)模型表达式如下
(5)
2.3. 组合模型
组合预测方法能够对各单一模型进行组合处理,从而得到一个含有各模型预测信息的新的预测模型,克服了利用单一模型预测的局限性。互联网货币基金收益率序列线性性质和非线性性质共存的特征尤其适合运用组合模型对其进行预测,以发挥各模型的最大优势,同时弥补单一模型预测的不足。
组合预测模型的输出结果是建立在具有差异化的各单个模型预测输出的基础之上的线性加权平均,使用组合模型进行预测时,首先假设具有
种不同的基础模型,其次假设组合模型的预测输出值为
,最后假设第
种基础模型的预测输出值为
。若设权重向量为
,则有组合预测模型如下
(6)
试图构造GARCH和BPNN两种方法的组合模型,则式(6)变为
(7)
其中,
,
,
分别为组合模型、GARCH模型和BPNN模型的预测输出值。
,
分别为GARCH模型和BPNN模型相应的权重值。
建立组合模型的核心是对于具有差异化的每个单个模型的权重进行估计,现有的确定权值的方法主要有等量权重、线性回归、方差最小化以及优势矩阵法。本文选用优势矩阵法对各模型权值进行估计。优势矩阵法具有更加良好的稳定性。
假定存在两种基础模型,令
指代在检验样本数据范围内模型1优于模型2的次数,
指代在检验样本数据范围内模型2优于模型1的次数。
,
和
分别表示两个基础模型的权值。若模型1为相应的BPNN模型,模型2为GARCH模型。则,组合模型为
(8)
3. 实证分析
3.1. 数据选取和评价标准
数据选取天弘增利宝(余额宝) 15~16年的每日万份收益率数据作为样本数据。样本数量为723。其中选取数据的70%作为训练样本,30%作为测试样本。数据来源于Wind数据库和天天基金网。
为更加直观的表现模型优劣,采用平均绝对误差(MAE)、均方误差(MSE)、平均误差(ME)、定向精度(DA)四个指标进行模型评估。表达式如下
(9)
(10)
(11)
(12)
其中,
,
分别为预测值和实际值。MAE、MSE、ME值是对实际值和预测值之间偏差的度量,故这三个指标越小,预测结果越好,模型越优。而DA表示定向精度,可以提供预测方向的正确性和预测精度。因此,DA的数值越大,预测输出的结果越好。
3.2. 建立GARCH模型
3.2.1. 描述性检验
金融时间序列通常具有尖峰厚尾和波动集聚的特征,不服从正态分布,需要利用ARCH类模型进行估计。因此,首先对样本数据进行正态性检验,从偏度、峰度以及JB统计量三个方面进行检验,结果由图1显示样本数据偏度为0.838927,峰度为2.177375,JB统计量为106.0666,JB统计量对应P值为0。故样本数据不服从正态分布。
其次,对样本数据进行平稳性检验,利用Eviews软件对收益率数据进行平稳性检验,结果如下。
由图2可知样本数据为非平稳时间序列,不可直接进行建模,故首先对样本数据进行一阶差分处理,一阶差分后的结果显示样本数据的一阶差分为平稳时间序列,平稳性检验见图。故需对样本数据的一阶差分序列进行时间序列建模。
由图3可看出,T统计量明显小于显著水平为1%的临界值,故序列已不存在单位根,具有平稳性。
3.2.2. GARCH模型的建立
首先对样本数据的一阶差分序列进行自相关性分析,由结果可知序列Q值大于200,相伴概率P值接近于0.000,序列存在自相关。故应选择自回归模型(AR)来进行数据拟合。
模型的定阶由样本数据一阶差分序列的自相关函数和偏自相关函数的拖尾和截尾特征初步断定,后根据AIC准则和SC准则进行选择。最终选择模型ARIMA(5,1,2)对样本数据进行拟合。经检验,模型中估计参数对应的P值均显著,说明利用该模型进行拟合是可靠的。
对残差序列进行ARCH-LM检验知,样本数据具有高阶ARCH效应,应建立ARCH(p)模型进行模拟,但最基本的ARCH(p)模型若是滞后阶数p较大,则需要估计很多参数,会损失样本容量。进而选择使用GARCH(1,1)模型进行建模,因为GARCH(1,1)模型等价于无穷阶ARCH(p)模型,因此常把高阶ARCH(p)模型简化为GARCH(1,1)模型。

Figure 1. Sample data descriptive chart
图1. 样本数据描述性统计

Figure 2. Yield sequence stability test
图2. 收益率序列平稳性检验

Figure 3. First order differential stability test
图3. 一阶差分序列平稳性检验
本文最终选择建立GARCH(1,1)模型拟合样本数据序列。预测模型为
均值方程
方差方程
拟合结果及预测结果如图4。
由图4可看出拟合模型对实际数据的拟合效果较好,但相对于样本数据,拟合模型比较平缓,对于极端数据的拟合度较差,对于非极端值的拟合度较好。模型预测图如图5所示。分析原因可能是由于互联网货币基金收益率的非线性特征导致。新型的互联网货币基金相较于传统的货币基金的波动集聚性特征还存在着波动持续性的特征。故以下引入BP神经网络模型对样本数据进行训练和预测。
3.3. 建立BP神经网络模型
3.3.1. BP神经网络各参数的确定
因为自回归阶数在一定程度上可以表示时间序列的历史数据和当前数据的输入输出关系。故根据时间序列模型确定的滞后阶数,联系神经网络应用的实际经验,确定BP神经网络输入神经元个数为4,建立4-10-1的BP神经网络。其中隐层神经元个数的确定根据经验公式
,其中
分别为神经网络输入输出神经元个数,
为0到10之间的常数,经试验确定为10。模型最大迭代次数设置为5000,学习率设置为0.02。
3.3.2. BP神经网络模型的预测
由MATLAB软件编程实现BP神经网络模型。其预测结果及残差图如图6。
图6所示为BP神经网络模型预测图。由图7预测残差图可看出残差在0周围上下波动,预测效果较好,但对于个别极端值的预测仍然不够精确,波动较大。
3.4. 建立BPNN-GARCH组合模型
假定
指代在检验样本数据范围中BP神经网络模型优于GARCH(1,1)模型的次数,
指代在检验样本数据范围内GARCH(1,1)模型优于BP神经网络模型的次数。
,
和
分别表
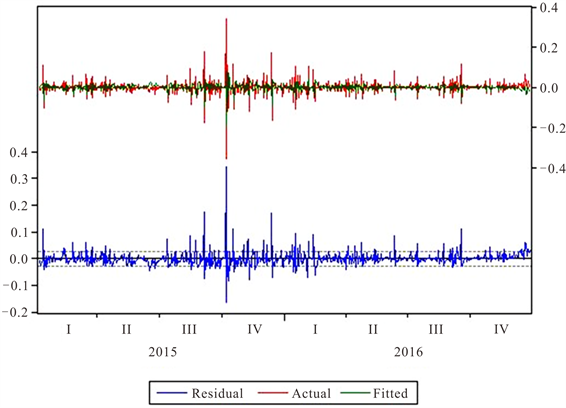
Figure 4. GARCH (1,1) model fitting renderings
图4. GARCH(1,1)模型拟合效果图

Figure 5. GARCH (1,1) model forecast graph
图5. GARCH(1,1)模型预测图
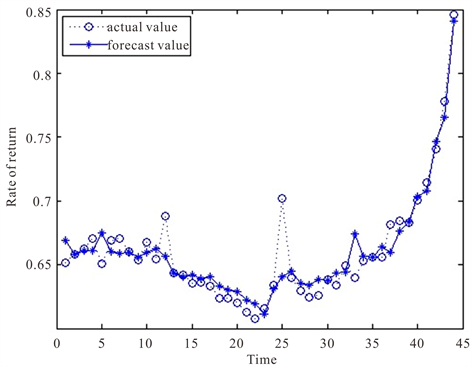
Figure 6. BP neural network model forecast graph
图6. BP神经网络模型预测图
示BP神经网络模型和GARCH(1,1)模型的权值。经计算
,即BP神经网络模型在组合模型中所占比重为56%,GARCH(1,1)模型在组合模型中所占比重为44%。则,组合模型为
利用组合模型对样本数据进行预测,结果如图8。
由BPNN-GARCH组合模型预测图即图8可看出,预测拟合效果较好。对于极端值的预测组合模型预测效果要优于GARCH(1,1)模型和BP神经网络模型的预测值。由图9残差图看出针对极端值的预测比两个单个模型效果要好,但仍有较少极端值不能精确拟合。
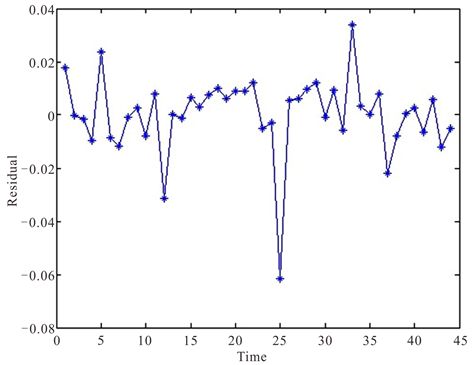
Figure 7. BP neural network model residual graph
图7. BP神经网络模型残差图
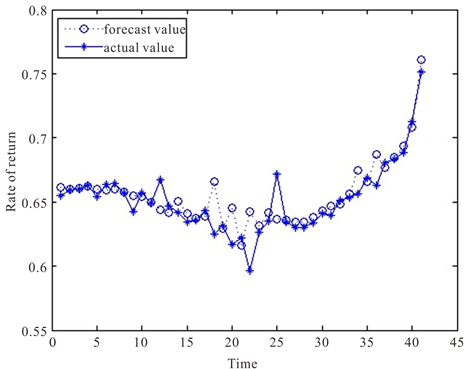
Figure 8. Combined model forecast graph
图8. 组合模型预测图
3.5. 结果分析
引入上述介绍的模型预测评价标准对模型预测效果进行比较,结果如表1。
表1显示,从MAE、MSE两个指标可以看出,BP神经网络模型和组合模型预测效果都优于GARCH模型,GARCH模型在传统时间序列的预测中有着不可忽视的优势,但互联网货币基金的收益率除了传统金融时间序列存在的尖峰厚尾及波动集聚性特征之外还具有波动持续性。这可能是GARCH模型预测效果不佳的一个原因。BP神经网络发挥了非线性映射及其自学习、自组织的优势,预测效果优于传统的GARCH模型。BPNN-GARCH组合模型在这两个指标中都优于两个单个模型,说明组合模型有效地结合了样本数据的线性因素和非线性因素,结合了BP神经网络模型和GARCH模型的优势。得到了优于两个单个模型的预测结果。
从ME指标看出,预测效果最好的是BP神经网络模型,而组合模型次之。单个模型与组合模型之间的差距不大。从DA指标看出组合模型预测效果要略好于两个单个模型。因预测精度(DA)衡量了模型预测方向的前后一致性,故从预测输出值误差和预测精准度两方面而言,组合模型相比于两个单个模型提供了更好的预测输出结果,其次是BP神经网络模型。
综上所述,BPNN-GARCH组合模型预测准确度在整体上要优于两个单个模型,更适合用于天弘增利宝(余额宝)收益率的预测。
4. 结束语
BPNN-GARCH模型在各项检验指标中有三项指标位均优于GARCH模型和BP神经网络模型。说明
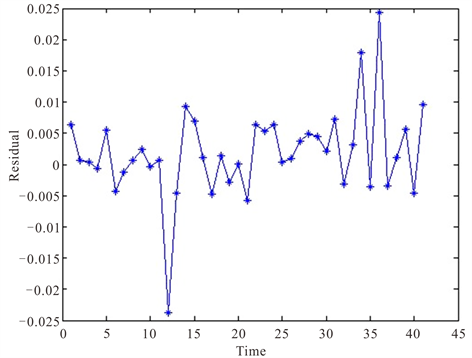
Figure 9. Combined model residual graph
图9. 组合模型残差图

Table 1. Comparison of prediction effect of each model
表1. 各模型预测效果比较
BPNN-GARCH组合模型在互联网货币基金余额宝的收益率预测中更具有优势。利用BPNN-GARCH组合模型对互联网货币基金进行收益率预测具有更高的准确率。但组合模型仍存在极端值预测不准确的问题,如何改进模型使其更加容易捕捉互联网货币基金收益率的极端值,仍需进一步的研究。
金融资产的风险表现为收益的不确定性,而这通常可以用收益率的波动性大小来衡量,本文对互联网货币基金的收益率进行了拟合预测,可以作为对互联网货币基金风险分析的基础。互联网货币基金作为新兴货币基金经过了四年发展它自身所存在的特殊风险也逐渐显现,对互联网货币基金的风险特征做一些细致的分析将有助于提高广大的投资者对互联网货币基金的认知程度。为广大投资者提供有效的投资建议,保护投资者的利益。