基于交叉算子和邻域搜索算子的离散粒子群优化算法

A Novel Discrete Particle Swarm Optimization Algorithm Base on Crossover Operator and Neighborhood Search

摘要: 基于交叉算子、邻域搜索算子和粒子群算法信息更新的本质机理，重新定义了粒子的基本运算，包含粒子位置的减法运算，粒子速度的数乘运算、加法运算以及粒子位置与速度的加法运算；提出了一种通用的新型离散粒子群优化算法；最后，以流水车间调度问题中23个标准算例为实验数据进行了仿真实验，实验结果表明了本文所提出算法的有效性。

Abstract: Based on crossover operator, neighborhood search and the essential mechanism of information updating in particle swarm optimization, a novel discrete particle swarm optimization (NDPSO) algorithm is proposed in which some basic operations on particles velocity and location are redefined. The NDPSO is a general-purpose optimizing model for combinatorial optimization problem; It is evaluated with 23 benchmark instances of flowshop scheduling problem and found to be more efficient and effective than existing algorithms.

1. 引言

粒子群优化(Particle Swarm Optimization, PSO)是Eberhard和Kennedy [1] [2] 于1995年提出的一种基于群体智能的新型优化算法，其思想来源于鸟群寻食行为，有依赖参数少、运算简单、易于实现，求解速度快等优点。PSO算法提出后，引起了智能计算等领域的学者们的广泛关注，并在短短的几年时间里涌现出大量的研究成果，已经被广泛的应用到各个领域，如神经网络训练 [3] 、调度问题 [4] 和模糊控制系统 [5] 等，成为智能计算领域的一个研究热点。

最初对PSO算法的研究主要集中在连续空间，即描述粒子状态及其运动规律的量都是连续的，并且在连续空间优化领域取得了巨大成功，因此许多学者试图用它去解决组合优化问题，但由于组合优化问题的离散特性，其求解效果不甚满意。因此对离散粒子群优化(Discrete Particle Swarm Optimization, DPSO)算法进行研究成为新的热点，对PSO算法的离散化研究可分为基于连续空间的DPSO和基于离散空间的DPSO两类 [6] 。1) 前者将实际离散问题映射到粒子连续运动空间后，在连续空间中计算和求解，算法生成的连续解与整数规划问题的目标函数评价值之间存在多对一的映射，导致大量冗余解空间与冗余搜索，从而影响算法的收敛速度。2) 后者则是将PSO算法映射到离散空间，在计算上以离散空间特有的对矢量的位操作取代传统向量计算，符合PSO的基本机理，不存在冗余搜索问题，且对离散问题表达自然。目前基于离散空间DPSO的研究主要有：Clerc等 [7] 提出了离散化PSO算法的框架，针对TSP问题重新定义了PSO的基本运算；Wang等 [8] 引入交换子与交换序列的概念，重新定义了PSO的基本运算；在文献 [8] 的基础上，Shi等 [9] 针对TSP问题引入了置换子与置换序列的概念，重新定义了PSO的基本运算。可是，现有研究主要针对个别类型问题(如，Traveling Salesman Problem, knap sack problem)，没有通用的标准模型 [6] 。

本文在上述研究的基础上，基于交叉算子、领域搜索算子和PSO算法信息更新的本质机理，针对组合优化问题，在PSO算法框架下，重新定义粒子的基本运算，提出了一种通用的新型离散粒子群优化(Novel Discrete Particle Swarm Optimization, NDPSO)标准模型，并利用仿真实验验证本文提出算法的有效性。

2. 标准PSO

Eberhard和Kennedy于1995年提出PSO后，该算法得到各领域学者的广泛研究。为了更好的控制算法寻优能力，1998年Shi等 [10] 进行了具有里程碑意义的研究，提出了惯性权重 $\omega$ ，用 $\omega$ 来控制速度变化，较大的 $\omega$ 可以加强PSO的全局搜索能力，较小的 $\omega$ 则能加强局部搜索能力。Shi等引入惯性权重的PSO被诸多学者称为标准PSO算法，可描述如下：

假设 $f\left(X\right)$ 是一个 $d$ 维的最小化优化问题，对第 $t$ 代的第 $i$ 个粒子在第 $d$ 维上的速度是 $v_{id}\left(t\right)\in \left[V_{\min },V_{\max }\right]$ ，其中 $V_{\min }$ 和 $V_{\max }$ 是依赖于问题的常数；位置为 $x_{id}\left(t\right)\in \left[X_{\min },X_{\max }\right]$ ，其中 $X_{\min }$ 和 $X_{\max }$ 为粒子搜索空间的边界； $p_{id}\left(t\right)$ 表示到目前为止第 $i$ 个粒子所搜索的最优位置； $p_{gd}\left(t\right)$ 表示到目前为止所有粒子所搜索的最优位置。粒子的速度和位置的更新方程如下：

$v_{id}\left(t+1\right)=\omega v_{id}\left(t\right)+c_1\xi \left(p_{id}\left(t\right)-x_{id}\left(t\right)\right)+c_2\eta \left(p_{gd}\left(t\right)-x_{id}\left(t\right)\right)$ (1)

$x_{id}\left(t+1\right)=v_{id}\left(t+1\right)+x_{id}(t),i=1,2,\cdots ,m,$ (2)

其中， $m$ 为粒子个数； $c_1$ 和 $c_2$ 分别为粒子的自学习系数和社会学习系数，统称为加速系数； $\xi$ 和 $\eta$ 为 $\left[0,1\right]$ 之间是随机数， $\xi ,\eta \in U\left(0,1\right)$ 。每一代最优位置的更新如下：

$P_i\left(t+1\right)=\{\begin{array}{l}{X}_i\left(t+1\right),\text{if}f\left(X_i\left(t+1\right)\right)<f\left(P_i\left(t\right)\right)\\ P_i\left(t\right),\text{otherwise}\end{array}$ (3)

The procedure of PSO is given as follows:

Step 1: Initialization

Step 1.1. Initialize iterative counter be $t=0$ , the $m$ random velocities $v_i\left(0\right)$ and the $m$ random positions $x_i\left(0\right)$ of the particles;

Step 1.2. Calculate $p_i\left(0\right)$ and $p_g\left(0\right)$ ;

Step 2: While termination criteria is satisfied do

Step 2.1. for ( $i=1;i<=m;i++$ ) {

Update $v_i\left(t\right)$ using (1);

Update $x_i\left(t\right)$ using (2);

Update $p_i\left(t\right)$ using (3);

If ( $f\left(p_i\left(t\right)\right)<f\left(p_g\left(t\right)\right)$ ) then $p_g\left(t\right)=p_i\left(t\right)$ ;

}//end for

Step 2.2. $t=t+1$ ;

Step 3: output.

3. 新型离散粒子群优化(NDPSO)

离散化粒子群优化算法的关键是如何定义PSO算法的基本运算规则 [7] ：位置的减法运算，即两个位置相减得到一个速度；速度的数乘运算，即一个数乘上一个速度后得到另一个速度；速度的加法运算，即两个速度相加得到另一个速度；粒子的移动，即位置与速度相加后得到一个新的位置。本节基于交叉算子、领域搜索算子和PSO算法信息更新的本质机理深入讨论该问题，提出一种新型的离散粒子群优化算法NDPSO。

3.1. 粒子位置与位置的减法及速度数乘的复合运算

在标准PSO算法的公式(1)中 $c_1\left(p_{id}\left(t\right)-x_{id}\left(t\right)\right)$ 与 $c_2\left(p_{gd}\left(t\right)-x_{id}\left(t\right)\right)$ 分别表示粒子的历史最优位置和群体的最优位置对粒子新位置的影响。粒子位置与粒子位置的减法运算结果为粒子的速度，相当于遗传算法中的交叉算子；然后分别根据粒子的自学习系数 $c_1$ 和社会学习系数 $c_2$ 对速度 $\left(p_{id}\left(t\right)-x_{id}\left(t\right)\right)$ 和速度 $\left(p_{gd}\left(t\right)-x_{id}\left(t\right)\right)$ 进行调节， $\xi$ 与 $\eta$ 相当于遗传算法中的交叉概率。

Murata等 [11] 提了置换流水车间调度问题最好的交叉算子(crossover for permutation flowshop scheduling, CPFS)：按交叉概率随机地从种群中选择两个个体作为父体，对于每个个体选取最先与最后回溯的工件位置作为交叉点，如果回溯工件个数小于(或等于) 1，则随机选择某两个(或一个)工件位置作为交叉点。首先将两个位置之前和之后的基因进行交叉复制，再按照父体中原来工件排列的顺序修补交叉部分中未包含的基因，该交叉操作既可以尽可能多地保留没有发生回溯的工件位置信息，又可以继承父染色体中工件之间的相对位置信息。如图1所示。

因此，定义粒子位置与位置的减法及速度数乘的复合运算 $V=c\times \left(X^a-X^b\right)$ 如下：

设速度 $V=\left(v_1,v_2,\cdots v_i,\cdots ,v_n\right)$ ，位置 $X^a=\left(x_1^a,x_2^a,\cdots x_i^a,\cdots ,x_n^a\right)$ ，位置 $X^b=\left(x_1^b,x_2^b,\cdots x_i^b,\cdots ,x_n^b\right)$ 均是 $n$ 维的行向量，常数 $c\in \left[0,1\right]$ 。 $V$ 的产生过程是生成 $\left[0,1\right]$ 之间的随机数 $rand\left(\right)$ ，若 $rand\left(\right)<c$ ，则以 $X^a$ 和 $X^b$ 为父体，随机选择某两个(或一个)工件位置作为交叉点，首先将两个位置之前和之后的部分进行交叉复制，然后按照父体中原来工件排列的顺序补齐交叉部分中没有包含的基因，再从两个子体中选取目标值较优的为 $V$ ；否则， $V=X^b$ 。

3.2. 常数与速度的乘法

在标准PSO算法中，常数与粒子速度的乘法运算结果为粒子的速度，相当于遗传算法中的变异算子。如，公式(1)中 $\omega v_{id}\left(t\right)$ 表示粒子的历史速度对新速度的影响，即惯性权重 $\omega$ 对速度 $\omega v_{id}\left(t\right)$ 的调节。公式(1)中 $\omega$ 、 $c_1\xi$ 和 $c_2\eta$ 相当于遗传算法中的变异概率。

在遗传算法中变异的目的是保持种群的多样性，邻域搜索是一种有效的求解大规模组合优化问题的优化方法，能够以初始解为基础遍历解空间，即其满足种群多样性的需求；特别地，通过邻域函数产生新解仍然在组合优化问题的解空间。邻域搜索算子主要包括移动Swap(x, y)、插入Insert(x, y)和3-opt等方式 [12] [13] 。如图2和图3所示。

Figure 1. CPFS process diagram

图1. CPFS过程示意图

Figure 2. Insert(x, y) process diagram

图2. Insert(x, y)过程示意图

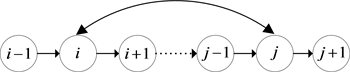
Figure 3. Swap(x, y) process diagram

图3. Swap(x, y)过程示意图

对于3-opt，任选节点 $i,j,k\left(i<j<k\right)$ ，删除边 $\left(i,i+1\right)$ ， $\left(j,j+1\right)$ ， $\left(k,k+1\right)$ ，为了避免将某部分路径反转(方向性变化使这部分路径的长度不可预计)，只能连接新边 $\left(i,j+1\right)$ ， $\left(j,k+1\right)$ $\left(k,i+1\right)$ 形成唯一的新路径，交换过程如图4所示，称这种3-opt为正方向3-opt (positive direction 3-opt, PD3opt)。

因此，定义常数与速度的乘法 $V^{\prime }=c\cdot V$ 如下：

设速度 $V^{\prime }=\left({v^{\prime }}_1,{v^{\prime }}_2,\cdots ,{v^{\prime }}_i,\cdots ,{v^{\prime }}_n\right)$ ，速度 $V=\left(v_1,v_2,\cdots ,v_i,\cdots ,v_n\right)$ 均是 $n$ 维的行向量，常数 $c\in \left[0,1\right]$ ， $1\le i\le n$ 。 $V^{\prime }$ 的产生过程如下：

Step 1：生成 $\left[0,1\right]$ 之间的随机数 $rand\left(\right)$ ， $\left[1,n\right]$ 之间的随机整数 $randInt\left(\right)$ ，令 $t=0$ ， $V^{\prime }=V$ ；

Step 2： $t++$ ; if $t\le randInt\left(\right)$ , then go to Step 3; otherwise, go to Step 4；

Step 3：if $rand\left(\right)\le c$ , then以 $V$ 为初始解，随机选取邻域搜索算子Swap(x, y)、Insert(x, y)和PD3opt进行邻域搜索，并根据目标函数值更新 $V^{\prime }$ ；otherwise, go to Step 4；

Step 4：stop, output.

3.3. 速度与速度加法的复合运算

在标准PSO算法中，粒子速度与粒子速度加法的运算结果为粒子的速度。并依据进化算法中“优胜劣汰”的基本规律。因此，定义 $V^{\prime }=V+V^p+V^g$ 如下：

设某粒子的当前速度 $V=\left(v_1,v_2,\cdots ,v_i,\cdots ,v_n\right)$ ，粒子与自己的历史最优位置运算所得速度 $V^p=\left(v_1^p,v_2^p,\cdots ,v_i^p,\cdots ,v_n^p\right)$ ，粒子与全局最优位置运算所得速度 $V^g=\left(v_1^g,v_2^g,\cdots ,v_i^g,\cdots ,v_n^g\right)$ ，粒子的新速度 $V^{\prime }=\left({v^{\prime }}_1,{v^{\prime }}_2,\cdots ,{v^{\prime }}_i,\cdots ,{v^{\prime }}_n\right)$ ，则以 $V$ 、 $V^p$ 和 $V^g$ 两两之间形成父体，选取CPFS算子以概率1进行优化，选择较优的子体为 $V^{\prime }$ 。

3.4. 速度与位置的加法运算

在标准PSO算法中，粒子速度与粒子位置加法的运算结果为粒子的位置。并依据进化算法中“优胜劣汰”的基本规律。因此，定义 $X^{\prime }=X\oplus V$ 如下：

设某粒子的当前速度 $V=\left(v_1,v_2,\cdots ,v_i,\cdots ,v_n\right)$ ，粒子的新位置 $X^{\prime }=\left({x^{\prime }}_1,{x^{\prime }}_2,\cdots ,{x^{\prime }}_i,\cdots ,{x^{\prime }}_n\right)$ ，则以 $V$ 与 $X$ 形成父体，选取CPFS算子以概率1进行优化，选择较优的子体为 $X^{\prime }$ 。

3.5. NDPSO中粒子速度和位置的更新公式

重新定义粒子的基本运算后，粒子速度和位置的更新公式如下：

Figure 4. PD3opt process diagram

图4. PD3opt过程示意图

$V_t^p=c_1\times \left(X^p-X_t\right)$ (4)

$V_t^g=c_2\times \left(X^g-X_t\right)$ (5)

$V_{t+1}=\left(\omega \cdot V_t\right)+V_t^p+V_t^g$ (6)

$X_{t+1}=X_t\oplus V_{t+1}$ (7)

其中，式(4)表示由粒子的第 $t$ 代位置向量 $X_t$ ，粒子自己的历史最优位置向量 $X^p$ 和粒子对局部最优解的信任概率 $c_1\in \left[0,1\right]$ ，计算第 $t$ 代的局部速度向量 $V_t^p$ ；

式(5)表示由粒子的第 $t$ 代位置向量 $X_t$ ，全局最优位置向量 $X^g$ 和粒子对全局最优解的信任概率 $c_2\in \left[0,1\right]$ ，计算第 $t$ 代的全局速度向量 $V_t^g$ ；

式(6)表示由粒子的第 $t$ 代速度向量 $V_t$ ，惯性权重 $\omega \in \left[0,1\right]$ ，局部速度向量 $V_t^p$ ，全局速度向量 $V_t^g$ ，计算第 $t+1$ 代的速度向量 $V_{t+1}$ ；

式(7)表示由粒子的第 $t$ 代位置向量 $X_t$ ，速度向量 $V_t$ ，局部速度向量 $V_t^p$ ，全局速度向量 $V_t^g$ ，计算第 $t+1$ 代的位置向量 $X_{t+1}$ 。

4. 仿真实验

4.1. 实验设计和参照算法

为了测试本文提出算法的性能，以23个无等待流水车间调度问题 [14] 标准算例为测试数据。采用VC++6.0作为编程语言实现NDPSO算法，实验在配置为Pentium3/CPU3.00GHz/RAM512M的台式机上进行。

NDPSO算法的基本流程与标准PSO算法相同，只是根据公式(4)、(5)、(6)和(7)更新种群。种群大小为100，最大迭代次数为500。每组实验独立运行30次，记录makespan 和CPU的平均值。

基于下降算法和禁忌搜索的DS + M算法和TS + M算法是文献 [11] 提出的五种算法中更有优势的两种算法；变邻域搜索算法VNS和模拟退火与遗传的混合算法GASA是文献 [15] 提出的算法；离散粒子群DPSO是文献 [16] 提出的算法。

4.2. 实验结果与分析

实验结果如表1所示，其中CPU表示算法结束所需的时间。PRD为所用算法与参考算法值相比的偏差， $\text{PRD}\left(\text{A}\right)=100\left(C^{\text{A}}-C^{\text{Ref}}\right)/C^{\text{Ref}}$ ，为了使结果具有可比性，本文借鉴上几种算法，以文献 [17] 中的RAJ作为参考值， $C^{\text{Ref}}$ 的取值为 $C^{\text{RAJ}}$ ，C^A代表算法A的makespan 值， $A\in \left\{VNS,GASA,DS+M,TS+M,IDPSO\right\}$ 。

从表1可知：

Table 1. Comparison of the experiment results obtained by various algorithms

表1. 各种算法实验结果比较

1) 在求解质量方面，本文提出的NDPSO算法明显优于其它算法。这表明本文基于粒子群基本优化机制的NDPSO算法具有良好的求解性能，可用于组合优化问题的求解。

2) 在计算时间方面，本文提出的NDPSO算法略差于DS+M算法、TS + M算法和DPSO算法，但明显优于VNS和GASA算法。

5. 结束语

粒子群算法是近年来发展起来的智能优化算法，因其在连续空间优化领域取得的巨大成功，使许多学者试图用它去解决组合优化问题。本文基于交叉算子、邻域搜索算子和粒子群算法信息更新的本质机理，重新定义了粒子的基本运算，包含粒子位置的减法运算、粒子速度的数乘运算、粒子速度的加法运算和粒子位置与速度的加法运算；给出了一种针对组合优化问题，通用的离散粒子群优化算法。最后，以23个标准算例为实验数据进行了仿真实验，实验结果表明了本文所提出算法的有效性。为了更好地求解组合优化问题，未来可进一步研究NDPSO算法的进化行为，如根据特定问题在基本流程中引入具有针对性的邻域搜索机制。

基金项目

国家社会科学基金西部项目(17XGL016)，宁夏自然科学基金(NZ17083)，宁夏高等学校科学研究项目(NGY2016085)，2017年宁夏医科大学优秀青年后备骨干培育对象(宁医校发【2017】119号)。