1. 引言
近年来,国内在役海底输油(气)管道发生安全事故,不仅影响了油气的正常生产,而且对海洋环境造成污染。研究发现,材料发生破坏或应力脆断时其承受的应力通常远远低于自身所能承载的极限应力,产生这一现象的主要原因是管道原结构存在一些细小裂纹 [1] 。在正常工作过程中,压力管道内壁产生裂纹并不是小概率事件,若其继续工作会导致裂纹进一步扩大,最终造成安全事故频发,甚至出现不可挽回的损失 [2] 。
目前,利用断裂力学理论分析管道安全的技术方法日趋成熟,数值计算方法被广泛应用于各个工程领域。其中,有限元法既不受所研究的裂纹体结构自身几何外形的影响,也不受结构自身承载复杂性的制约,在断裂力学中其有着更为广泛的发展前景 [3] 。本文对含有斜裂纹的压力管道建立有限元模型,通过计算求解出含斜裂纹管道的应力强度因子的有限元解,得到裂纹体结构裂纹尖端附近的应力应变场,以方便工程实际应用。
2. 管道模型参数
在实际工程中,复杂裂纹较为常见,包括斜裂纹、分叉裂纹和平行裂纹。其中,斜裂纹最为常见,指裂纹与轴向夹角θ ≠ 0˚ [4] ,本文仅对该类裂纹进行分析 [5] 。分析过程中,确定含斜裂纹压力管道的诸多边界约束条件,充分考虑裂纹尖端应力强度因子的影响因素,以建立不同参数条件下的管道模型并求解。
综合考虑各种因素后的管道模型参数设置:管道长度L = 1000 mm、壁厚t = 1 mm、管道直径D = 400 mm、半裂纹长度a = 10 mm;裂纹与轴向夹角θ = 45˚;管道材质35号钢;弹性模量E = 2.01E11;泊松比0.3;剪切模量0.794E11;屈服应力315 MPa;管道内压1.5 MPa (内压作用时,两端为轴向约束) [6] 。建立的含斜裂纹压力管道几何模型见图1,两端视为轴向约束,模拟计算时对整个结构进行力学分析。

Figure 1. Geometric model of pressure piping inclined crack
图1. 含斜裂纹压力管道几何模型
3. 有限元建模
利用有限元法分析裂纹在管道轴向贯穿时的应力场,在线弹性条件下,求出内压作用下的裂纹尖端应力场 [7] 和裂纹应力强度因子K,以满足实际工程中对断裂参数的需要。
采用Shell63单元对薄壁管道建模。通常情况下,二维裂纹在划分单元之后可以直接利用KSCON命令对裂纹尖端单元进行奇异化处理,但三维裂纹不能直接利用该命令来生成裂紋前缘处的奇异单元,需要寻求其他方法对三维裂纹建模。工程中主要采用实体建模法,具体思路是将含裂纹管道分为含裂纹的小块模型M和管道主体部分N,并分别建模,然后利用ANSYS中的Boolean运算对两部分进行Glue (黏接运算)操作,先对含裂纹的小块模型M进行细腻的网格划分,再利用自由划分方法对不含裂纹的管道主体部分N划分网格。
由于存在应力集中,裂纹尖端周围区域的应力、应变值的跨度很大,需要适当加密裂纹尖端周围的有限元网格,以获得更准确可靠的应力、应变和位移场。通常情况下,裂纹前缘第一层单元垂直方向的长度不能超过裂纹长度的5%,裂纹体裂纹尖端附近区域单元最大长度与最小长度的比值不能超过5,但在远离裂纹尖端的区域该比值可以控制在20之内。
网格划分之前,需要在裂纹尖端创建奇异点,并设置奇异单元 [8] ,1个平面中只能设置1个奇异点。本文为创建2个奇异点的全裂纹,管道建立坐标系后,通过Glue (黏接运算)命令建立裂纹共享的边界。管道网格划分见图2、图3。
4. 模型载荷施加
根据第四强度理论,管道模型整体应力求解结果见图4,裂纹尖端受力情况见图5。
从图5中可以看出:最大应力值位于两个裂纹尖端附近;裂纹尖端附近的应力值随着其与裂纹尖端距离的增大而减小,但仍然远远大于远离裂纹尖端处的应力值(该变化规律正好对应于裂纹尖端附近接近呈对称分布的蝶形高应力区域);最小应力值位于裂纹两个尖端之间靠近裂纹线的部位(图中深蓝色区域)。

Figure 2. The meshing of tip oblique crack
图2. 斜裂纹尖端网格划分

Figure 3. Overall grid partition of pressure piping inclined crack
图3. 含斜裂纹管道整体网格划分

Figure 4. Overall stress condition of pressure piping
图4. 管道整体应力情况
5. 斜裂纹应力强度因子变化规律
利用平面位移外推法在全模型中求解应力强度因子K。以裂纹与轴向夹角θ = 45˚、管道模型长度L = 1000 mm、管道直径D = 400 mm、半裂纹长度a = 10 mm、管道壁厚t = 10 mm、管道内压P = 1.5 MPa为基本参数创建有限元模型,然后分别以其中一个参数为变量、其余参数为定量,建立不同参数条件下

Figure 5. Stress condition of tip oblique crack
图5. 斜裂纹尖端应力情况
含有斜裂纹(θ ≠ 0)的压力管道有限元模型并计算求解,探求该变量与应力强度因子K的变化规律。
5.1. 管道内压P的影响
分别取θ = 45˚,a = 10 mm,D = 400 mm,L = 1000 mm为定量,管道壁厚分别取t = 10 mm和t = 15 mm,管道内压P作为自变量,分别取作P = 0.5、1、1.5、2、2.5、3、3.5、4 MPa,建模计算出对应的应力强度因子KI和KII值并作出曲线,结果见图6。(KI和KII不同壁厚下的强度因子)
从图6中可以看出:不同壁厚条件下应力强度因子KI和KII的曲线走势基本相同;随着管道内部压力的增大,应力强度因子KI和KII均增大,基本呈线性增长关系,即KI、KII与P值呈增函数关系。
5.2. 管道壁厚t的影响
半裂纹长度分别取a = 10 mm和a = 20 mm,管道壁厚t作为自变量,分别取1 mm、3 mm、5 mm、10 mm、15 mm、20 mm、25 mm、30 mm,其他参数为定量,建模计算应力强度因子KI、KII与不同壁厚t的关系曲线,结果见图7。
从图7中可以看出:半裂纹长度不同,但两种应力强度因子KI、KII的走势基本接近;随着管道壁厚t的增大,应力强度因子KI和KII整体呈减小的趋势,壁厚由1 mm增加到5 mm,KI、KII值迅速减小,壁厚超过5 mm后,KI、KII值减速变缓。
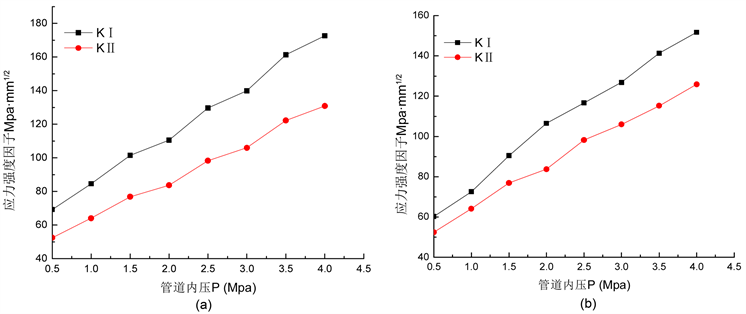
Figure 6. Relationship curves of K and pipeline internal pressure P. (a) t = 10 mm; (b) t = 15 mm
图6. K和管道内压P的关系曲线。(a) t = 10 mm;(b) t = 15 mm
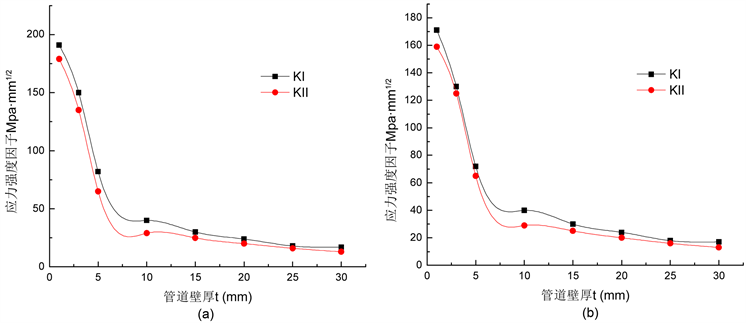
Figure 7. Relationship curves of K and pipe wall thickness t. (a) a = 10 mm; (b) a = 20 mm
图7. K和管道壁厚t的关系曲线。(a) a = 10 mm;(b) a = 20 mm
5.3. 半裂纹长度a的影响
管道壁厚分别取t = 10 mm和t = 15 mm,半裂纹长度a作为变量,分别取12 mm、16 mm、20 mm、24 mm、28 mm、32 mm、36 mm、40 mm,其他参数为定量,建模计算应力强度因子KI、KII与不同半裂纹长度的变化曲线,结果见图8。
从图8中可以看出:不同壁厚条件下,应力强度因子KI和KII值的曲线走势基本相同;随着半裂纹长度a值的增加,应力强度因子KI、KII不断增大,与半裂纹长度近似呈线性增长关系。
5.4. 管道直径D的影响
半裂纹长度分别取a = 10 mm和a = 20 mm,管道直径D作为变量,分别取200 mm、250 mm、300 mm、350 mm、400 mm、450 mm、500 mm、550 mm,其他参数为定量,建模计算应力强度因子KI、KII随不同管道直径的变化曲线,结果见图9。
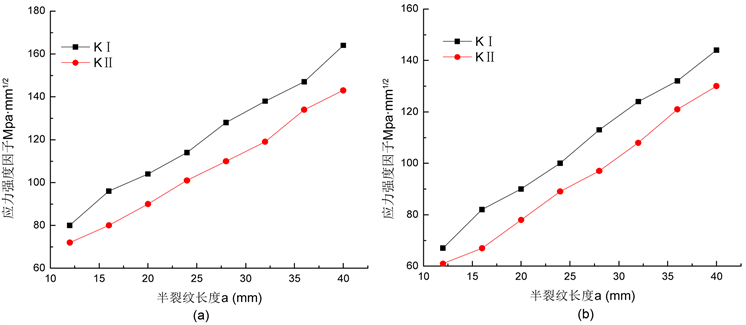
Figure 8. The relationship between K and semi-crack length a. (a) t = 10 mm; (b) t = 15 mm
图8. K和半裂纹长度a的关系曲线。(a) t = 10 mm;(b) t = 15 mm

Figure 9. The relationship between K and semi-crack length D. (a) a = 10 mm; (b) a = 20 mm
图9. K和半裂纹长度D的关系曲线。(a) a = 10 mm;(b) a = 20 mm
从图9中可以看出:两种应力强度因子KI、KII的走势基本接近,总体上随着管道直径的增加而增大;管道半径在300~500 mm时,KI和KII增速较快。
5.5. 裂纹夹角θ的影响
半裂纹长度分别取a = 10 mm和a = 20 mm,裂纹线与管道轴线夹角θ作为变量,分别取0˚、10˚、20˚、30˚、40˚、50˚、60˚、70˚、80˚、90˚,其他参数为定量,建模计算应力强度因子KI、KII随裂纹线与轴向夹角θ的关系曲线,结果见图10。
从图10中可以看出;应力强度因子KI随着裂纹夹角θ的增加而减小;在0˚~45˚,KII随着θ的增加而增大,在45˚~90˚,则随着θ的增大而减小,在θ = 45˚附近KII出现最大值;在0˚~45˚,应力强度因子KI总体上大于KII,且角度越小二者的差值越大;θ = 0˚时(即为轴向裂纹),应力强度因子KI恒大于KII,且角度越大两者之差越小。
5.6. 管道直径与壁厚比值的影响
管道壁厚分别取t = 10 mm和t = 15 mm,管道直径与管道壁厚的比值依次取D/t = 12、16、20、22、24,其他参数为定量,建模计算应力强度因子KI和KII与管道直径与壁厚比值的关系曲线,结果见图11。
从图11中可以看出:不同壁厚条件下,应力强度因子KI和KII的曲线走势基本相同,并随着比值D/t的增加而增大;两种应力强度因子与管径与壁厚比值呈线性增长关系。
6. 结论
1) 在线弹性条件下建立了含有斜裂纹压力管道的有限元模型,在内压载荷条件下求出应力强度因子K,分析了不同因对其影响规律。
2) 在管道直径相同的前提下,管径与壁厚的比值越大(即壁厚越小),应力强度因子KI和KII的值越
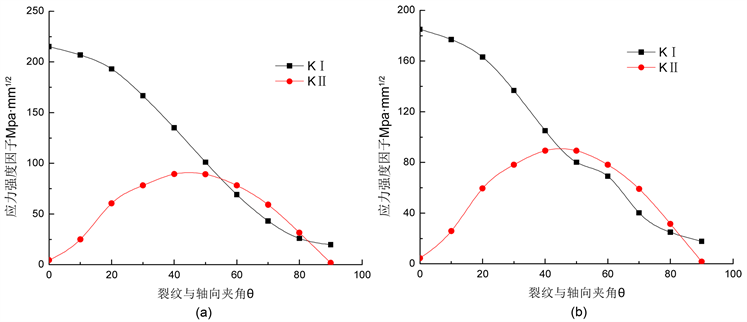
Figure 10. The relation curve of K and crack angle θ. (a) a = 10 mm; (b) a = 20 mm
图10. K和裂纹夹角θ的关系曲线。(a) a = 10 mm;(b) a = 20 mm
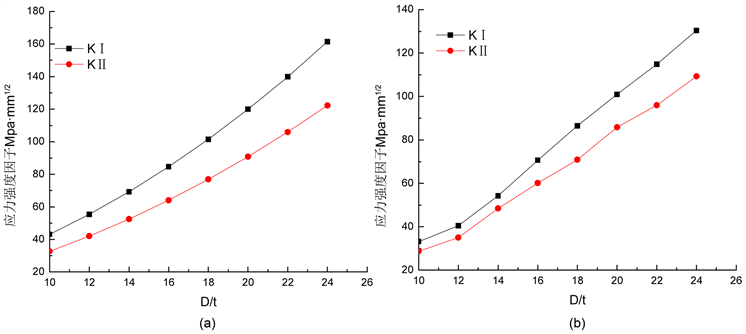
Figure 11. The relationship between K and pipe diameter and wall thickness ratio D/t. (a) t = 10 mm; (b) t = 15 mm
图11. K和管径与壁厚比值D/t的关系曲线。(a) t = 10 mm;(b) t = 15 mm
大,管道的安全性越低,即含裂纹的薄壁管道更容易引发断裂事故。
3) 本文的分析结果填补了应力强度因子KI和KII的计算空缺,增补了部分形状因子FI和FII的数据库,对后续含斜裂纹压力管道的深入研究奠定了一定基础,计算得到的规律和拟合的相关公式在工程实际中有着很强的应用价值。