1. 引言
1978年,Koenker and Bassett [1] 首次提出了用分位数回归方法来描述因变量的条件分位数与自变量之间的关系。分位数回归的提出引起了广泛的关注。分位数回归被广泛应用于农业、基因芯片技术、生存研究、经济学、医疗卫生、环境科学等领域。
在分位数回归估计中,算法的实现起着至关重要的作用。分位数回归模型估计方法中较经典的方法有Yu和Moyeed在2001年提出的单纯形法和内点法。其他的估计方法还有参数化方法和非参数方法。
有序数据在对事物分类的同时给出了各类的顺序,其数据仍表现为“类别”,但各类之间是有序的,可以比较优劣但其数值的大小差值却无意义。
在大多数研究领域中都会用到有序数据。目前已有大量的文献对有序数据进行了研究,但是用贝叶斯方法对有序数据进行分析目前还鲜少有人提及。
2. 贝叶斯分位数回归
对于一个随机变量x,如果它服从参数为
的非对称拉普拉斯分布(Asymmetric Laplace distribution, ALD),那么其密度函数可以写为
(1)
其中
为位置参数,
为尺度参数,
为偏度参数。
引理 如果随机变量
则其方差
。
证明 由于
且
根据函数
其中
,经计算可得
证毕。
如果随机变量
,则其分位数函数(分布函数的逆函数)为
(2)
从上式中可以的到一个很重要的性质:
(3)
即服从非对称拉普拉斯分布的随机变量在概率
处的分位数等于位置参数
。
设
服从如下的线性回归模型,
(4)
式中
是在观测到
的条件下,
在
概率水平下的分位数,
是参数向量,误差项
相互独立且服从非对称拉普拉斯分布,即
。依据非对称拉普拉斯分布的
线性变换性质,式(4)可以等价表示为
故
的密度函数为:
(5)
。样本的似然函数可以表示为
(6)
其中
为损失函数
.
设参数
和
相互独立,其先验密度分别为
和
。根据贝叶斯定理,参数
的联合后验密度为
(7)
在已知的文献中,如Yu等 [2] ,在估计过程中将尺度参数设定为常数1。但在实际应用中,将尺度参数设为常数缺有欠妥当。若尺度参数定为常数1,则随机变量的方差将不小8。在实际的数据研究中这个约束条件的存在并不合理。事实上,尺度参数的存在使得服从非对称拉普拉斯分布的随机变量的方差能取任意正值。尺度参数影响了参数估计的质量,在实际的应用当中,它应该被当为待估参数去处理,而不是主观地被设为某个常数。
对于分位数回归中的参数,它们不存在标准的共轭先验分布。这导致在贝叶斯推理中获取参数的后验分布解析表达式有一定的困难。若选择的参数的先验分布能确保参数的后验分布为真实分布,我们就可以利用MCMC 模拟得到参数的估计。
在Yu的研究中 [2] ,尺度参数为常数时,参数
的先验分布是非真实均匀分布,得到的联合后验分布为真实分布。考虑到尺度参数的参数化,在无信息的前提下,参数的先验分布存在很多种可能,而被选择的先验分布可能会是非真实的分布。在这种情况下,参数
与
满足什么条件会使得后验联合分布为真实分布。这对贝叶斯推理是很重要的一环。而下面的定理就可以保证后验分布是真实分布。
定理 对于任意
,参数的似然函数由式(6)给出,
和
的先验密度分别为
和
。若
服从不真实均匀分布,
满足
则参数的联合后验分布
是一个真实分布,即满足条件
证明 根据式(6)与(7)有
可以推知
于是
非真实先验分布是在贝叶斯推断中在无信息先验情况下常采用的一种先验分布形式,参数
服从非真实先验分布,则其概率密度的积分是无穷大的 [3] ,即
可得
因此
证毕。
3. 有序数据模型
有序数据的分位数回归模型能够用连续的潜变量
来表示
(8)
其中,
是
维的协向量,
是
维的未知参数向量,误差项
。
表示观测值的个数。潜变量与我们观测到的响应变量
存在一定的关系,且响应变量有
个指标。我们用割点向量
来反应
和
的关系:
其中
,
。一般而言
常被设定为0 [4] 。对于给定的数据
,模型的似然函数能够用包含有未知参数
的函数表示
其中
表示非对称拉普拉斯分布的分布函数。
为示性函数。
为了在分位数回归中得到吉布斯算法,关于非对称拉普拉斯分布,Kozumi和Kobayashi在2011年 [5] 给出了一个基于指数分布和正态分布的混合表达式。若
,则有
(9)
其中
和
相互独立,
,
,
表示指数分布。式(9)中的常数项
为
非对称拉普拉斯分布的混合表达式使得在研究过程中,可以直接利用正态分布的性质。而这将对有序数据分位数回归模型的分析起到重大的作用。
贝叶斯方法来估计分位数回归模型运用到了潜变量表达式 (8)与非对称拉普拉斯分布的混合表达式(9),
分位回归模型能够表示为
(10)
上式中可以看出潜变量的条件分布服从正态分布,即
。这使得我们在估计
过程当中,能够利用正态分布的性质来进行研究。
考虑结果拥有三个指标的情况,回归模型能够用下式表示
(11)
其中
是
分位水平下的尺度参数,割点向量
满足条件
,且
为某固定常值。
对于回归模型(11),潜变量
的条件期望包含了尺度参数
,这导致模型不能直接利用吉布斯抽样方法进行估计,但对模型进行简单的变形之后就能消除尺度参数的影响从而能利用吉布斯抽样方法来进行估计。模型(11) 能表示为
(12)
其中
,因此潜变量的条件分布服从正态分布,即
。接下来,
就是要设定参数的先验分布来获得参数的后验分布。设定参数的先验分布为:
其中
和
分别表示逆伽玛分布与指数分布。通过贝叶斯定理,参数
的联合后验密度为:
当切割点与潜变量已知的情况下,观测值
不依赖于
,根据式(12),潜变量
的条件密度
满足
。待估参数的后验密度为
据此,我们就能根据后验密度来导出我们感兴趣的参数的条件后验密度。
的条件后验密度
正比于
设
,
则有
经过简单的变形有
因此
结果表明,
的条件后验分布为正态分布,即
。
尺度参数
的条件后验密度
正比于
其中
,
。
的条件后验分布为逆伽玛分布即
。
的条件后验密度
正比于
且
有如下形式
设
,
则有
的条件后验分布为广义逆伽玛分布,即
。
4. 数据模拟分析
我们从如下模型获得观测值
与
的先验分布为
,尺度参数
的先验分布设定自由度为3的卡方分布。采用Gibbs抽样法共模拟5000次,为消除初值对抽样分布的影响,去掉前2000个抽样值。在应用Gibbs抽样算法对参数进行抽样时,特定参数的Gibbs模拟值是否是真实后验分布的合理近似,这对参数估计值的正确性意义重大,因此在统计推断之前需要对抽样分布进行检验。
图1给出了样本容量为100时,
,
和
在0.5分位点下的MCMC抽样值轨迹和核密度图。图中显示三个参数的3000个抽样值序列在某一个值的上下波动,因此抽样构成的马尔科夫链收敛
图2给出了样本容量为100时,
,
和
在0.5分位点下抽样值的自相关图。从图中可以看出随着滞后期的增加,自相关系数趋向于零。
综上,马尔科夫链收敛且自相关系数趋于零,所以在样本容量为100,各参数的贝叶斯中位数回归估计结果是可靠的。其他样本容量和分位点下的马尔科夫链均收敛,自相关系数也趋于零。表1和表2给出了不同样本容量下得到的MCMC参数估计结果。
在表1和表2中。比较
,
和
参数化与未参数化下的估计结果,可以发现在一定的样本容量,特定的分位点下,当
被参数化时,
和
的抽样标准差均小于
未参数化是各自的标准差。这表明尺度参数的参数化可以提高被估系数的精确度,从而提高待估系数假设检验的准确性。因此在用Gibbs抽样方法进行贝叶斯分位数回归估计是应该将尺度参数参数化,而不是设定为常数。此外,还可以发现,

Figure 1. The MCMC trace plots and the density of
图1.
的MCMC抽样值轨迹和核密度图

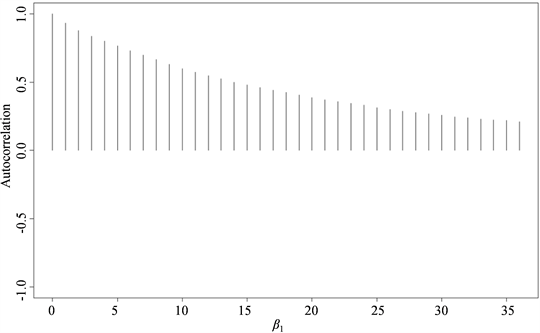

Figure 2. The autocorrelation of
图2.
抽样值的自相关图

Table 1. Estimation of β 0 in different situation
表1.
在不同分位数水平下的估计量

Table 2. Estimation of β 1 in different situation
表2.
在不同分位数水平下的估计量
注:给定样本容量,未参数化和参数化情形下的数字特征中,第一行表示参数的真值,第二行和第三行数值分别表示参数估计量分布的均值和标准差。
在给定样本容量的情况下,无论
是否参数化,
的标准差总是小于同一分位数水平下
的标准差。对于
,无论尺度参数是否被参数化,它的精度都随着样本量的增加而提高。