基于极限载荷与断裂强度的5A06铝合金焊接缺陷安全性评定的数值方法研究

Numerical Method Study on Safety Assessment of Welding Defects of 5A06 Aluminum Alloy Based on Ultimate Load and Fracture Strength

摘要: 本文建立了一种针对5A06铝合金带焊接缺陷平板的安全性评定的数值方法。首先采用极限载荷分析法建立了极限应力和裂纹长度的定量关系，从而获得失效评估曲线(FAC)。对130 mm厚的5A06铝合金对接焊接平板，采用SINTAP标准获得焊接残余应力分布和残余应力强度因子,并用虚拟裂纹闭合技术(VCCT法)计算工作载荷作用下的应力强度因子，建立了5A06铝合金失效评估图(FAD)。论文提出的数值方法能够对给定缺陷条件下的承载能力进行安全性评定；相反，在给定外载荷条件下，对缺陷的容纳限值进行确定。

Abstract: In this paper, a numerical method for assessment the safety of 5A06 aluminum alloy strip with welded defects is established. First, the quantitative relationship between the limit stress and the length of the crack is established by the limit load analysis method, and then the failure assessment curve (FAC) can be obtained. For the 130 mm thick 5A06 Aluminum Alloy butt welding plate, welding residual stress distribution and residual stress intensity factor are obtained by SINTAP, and the stress intensity factor of the working load is calculated by the virtual crack closure tech-nique (VCCT method), then the 5A06 Aluminum Alloy failure assessment diagram (FAD) is estab-lished. The numerical method proposed in this paper can be used to evaluate the safety of the bearing capacity under the condition of a given defect. On the contrary, under the given external load conditions, the limitation of the defect can be determined.

1. 引言

焊接工艺已广泛运用于机械制造中，焊接接头作为结构构件中的薄弱环节，其安全性很大程度上影响到结构整体的安全程度。虽然现在焊接工艺越来越成熟，但焊接结构构件中要获得无缺陷的焊接接头，在技术上是相当困难的，也是不经济的，故焊接构件避免不了存在残余应力与焊接缺陷(孔洞、裂纹)。因此研究焊接结构构件满足使用要求下，将缺陷限制在多大的范围之内，使其对焊接结构构件的运行不致产生危害成为了一个重大课题。

自从Dowling和Townley基于“合于使用原则”提出失效评估图(FAD)技术 [1] 以后，因其同时考虑塑性破坏与脆性断裂而得到了广泛认可并迅速的得到发展，之后围绕着FAD技术的研究工作从未间断。如考虑循坏加载 [2] 和混合加载 [3] 、高温和蠕变 [4] 、概率与可靠性 [5] [6] 、多裂纹 [7] 和韧性断裂 [8] 等的FAD评估。一些知名机构也基于FAD建立起了规范与标准，如API 579，BS 7910，CEGB R6，JEME和SINTAP。并后续有基于规范进行比较验证与改进的研究工作。如基于应变的FAD评估 [9] [10] 、针对三维面裂纹提出的统一约束参数的FAD评估 [11] 。现失效评估图(FAD)技术可应用于管道与压力容器 [12] - [21] 等众多领域的安全性评估当中。

虽然FAD技术应用广泛，然而针对焊接构件的FAD评估还有待进一步深入，当前很多的研究工作都是围绕着规范进行，如潘建宾 [22] 等运用R6规范讨论了裂纹位置对承载能力的影响，王元清 [23] 等人介绍SINTAP的FAD评估步骤，并与断裂判据K_IC进行了对比。Yun-Jae Kim等人 [24] 阐述了欧洲工业结构完整性评定方法(SINTAP)中对于焊接接头强度不匹配的缺陷评定方法，给出了该方法的有限元和实验验证。其众多研究说明了标准的可靠性，然而规范的评价体系是同时满足多数材料的FAD评估，故针对部分材料的安全性评估十分保守，经济性差。故探究一种灵活的、针对各种材料的安全评估方式是十分有意义的。

本文对130 mm厚的5A06铝合金对接焊接平板，采用SINTAP标准获得焊接残余应力分布和残余应力强度因子，并用虚拟裂纹闭合技术(VCCT法)计算工作载荷作用下的应力强度因子，建立了5A06铝合金失效评估图(FAD)。论文提出的数值方法能够对给定缺陷条件下的承载能力进行安全性评定。

2. 失效评估曲线(FAC)的数值确定方法

2.1. 材料5A06铝合金力学性能参数

模型的材料为广泛用于航空航天等重要领域的5A06铝合金，模型为厚130 mm的超厚平板，焊接方式采用多层填丝激光焊(如图2所示)，根据相关研究发现，其焊接接头拉伸强度可达到母材的93%以上，延伸率为基材的58%左右 [25] ，故可在进行有限元分析时，焊缝区域的材料和母材区域材料取同一应力应变曲线。通过有限元商业软件ANSYS计算板件存在不同长度的中央裂纹下应力应变场，并为评估提供数据。

5A06铝合金板的应力应变曲线如图1所示 [26] ，相关的力学性能参数如表1所示。

2.2. 有限元模型

针对图2所示的平板对焊工艺为：首先是激光自熔焊接区，然后是激光填丝焊。设模型中间位置存在穿透型平面裂纹，可将计算模型简化为二维带裂纹模型。

由于模型具有对称性，故可取1/4模型进行计算，使用四边形八节点单元(plane183)，为保证计算精度，对于裂纹前沿做网格的局部细化，模型共39675个单元，划分网格及约束如图3所示。

Figure 1. Real stress-strain curve of 5A06 aluminum alloy

图1. 5A06铝合金真实应力应变曲线

Table 1. Mechanical properties of 5A06 aluminum alloy

表1. 5A06铝合金材料力学性能

Figure 2. 3D model of 5A06 aluminum alloy plate with penetrating crack

图2. 5A06铝合金平板含穿透裂纹三维模型

Figure 3. Meshing of two dimensional model with central crack

图3. 含中央裂纹二维模型网格划分

3. 失效评估曲线(FAC)

3.1. 带裂纹5A06铝合金板确定极限应力σ_NC

采用含中央穿透型裂纹平板确定5A06铝合金极限应力 ${\sigma }_{NC}$ 和FAC，矩形板的尺寸长为200 mm，宽为160 mm，半裂纹长度分别取为4 mm，8 mm，12 mm，16 mm，20 mm。采用有限元方法计算获得的加载端应力(图3中的P)与最大应变的关系曲线如图4所示。极限应力 ${\sigma }_{NC}$ 的确定方式为：求出载荷—应变曲线的弹性斜率，然后作出五倍弹性斜率直线，极限应力 ${\sigma }_{NC}$ 定义为两线相交处的应力值 [27] 。采用以上方法确定的5A06铝合金不同裂纹长度下的极限应力 ${\sigma }_{NC}$ 如表2所示。通过表2的数据，获得无因次极限应力比 ${\sigma }_{NC}/{\sigma }_0$ 与裂纹长度与板宽比 $2c/W$ 的关系曲线如图5所示，通过数据拟合，得到其函数关系式为：

$\frac{{\sigma }_{NC}}{{\sigma }_0}=0.43+0.4e^{20c/W}+0.18e^{66.7c/W}$ (1)

式中： ${\sigma }_0$ 为不带裂纹的极限应力， ${\sigma }_{NC}$ 为带裂纹的极限应力，c为半裂纹长度，W为板的宽度。

3.2. FAC的确定方法

根据上节的公式(1)，由极限载荷分析法得到平板在特定裂纹长度下的极限应力 ${\sigma }_{NC}$ ；通过公式(3)获得有限宽板修正因子，利用公式(2)换算得到无限宽板下的极限载荷 ${\sigma }_{NC}^{\infty }$ 。利用几组不同裂纹下的极限载荷 ${\sigma }_{NC}^{\infty }$ 和无缺陷存在下板的极限载荷 ${\sigma }_0$ ，代入基于固有缺陷模型 [28] 得到的FAC关系式(5)，拟合获得常数 ${\delta }_{aci}$ 和 $K_{IFM}$ ，即可确定出FAC。

Figure 4. Load-end tress and maximum strain curve with different crack lengths

图4. 不同裂纹长度对应的加载端应力与最大应变曲线

Table 2. Ultimate stress σ N C with different cracks

表2. 不同裂纹下的极限应力 ${\sigma }_{NC}$

Figure 5. The relationship between the limit stress ratio and the dimensionless crack length

图5. 极限应力比与无量纲裂纹长度的关系曲线

${\sigma }_{NC}^{\infty }={\sigma }_{NC}Y$ (2)

$Y=\sqrt{\sec \left(\frac{\pi c}{W}\right)}$ (3)

$K_Q\equiv {\sigma }_{NC}^{\infty }\sqrt{\pi c}$ (4)

$K_Q=K_{IFM}\left[1-{\delta }_{aci}\left(\frac{{\sigma }_{NC}^{\infty }}{{\sigma }_0}\right)\right]\sqrt{1-{\left(\frac{{\sigma }_{NC}^{\infty }}{{\sigma }_0}\right)}^2}$ (5)

根据文 [29] ，裂纹长度与板宽之比2c/W > 0.086时，材料的破坏主要由塑性极限载荷控制；当2c/W ≤ 0.086时，材料的破坏主要由断裂准则控制。故本文使用极限载荷分析获得FAC曲线时，将2c/W控制在0.025以下以保证其合理性。通过式(1)得到不同裂纹长度下的极限载荷 ${\sigma }_{NC}$ 后，使用公式(2)与公式(3)转换为无限宽板的极限载荷值 ${\sigma }_{NC}^{\infty }$ ，再通过公式(4)计算得到对应的应力强度因子 $K_Q$ ，最后利用公式(5)拟合曲线可得到断裂参数 $K_{IFM}$ 与 ${\delta }_{aci}$ 如表3所示。获得的FAC曲线的函数关系式为：

$K_Q=47\left[1-0.2102\left(\frac{{\sigma }_{NC}^{\infty }}{{\sigma }_0}\right)\right]\sqrt{1-{\left(\frac{{\sigma }_{NC}^{\infty }}{{\sigma }_0}\right)}^2}$ (6)

根据公式(6)，画出5A06铝合金的失效评估曲线如图6所示。

4. 构建失效评估图(FAD)

由焊接引起的裂纹缺陷的安全性评估使用的失效评估图(FAD)包含两部分，第一部分失效评估曲线(FAC)。第二部分失效评估点(FAP)参数。含中央穿透型裂纹的5A06铝合金板的失效评估曲线已经通过前面计算获得(图6所示)，以下将通过计算获得失效评估点(FAP)参数，以构成失效评估图，对含缺陷构件进行安全性评估。

Table 3. Fitting value of fracture parameters K I F M and δ a c i of 5A06 aluminum alloy

表3. 5A06铝合金断裂参数 $K_{IFM}$ 和 ${\delta }_{aci}$ 的拟合值

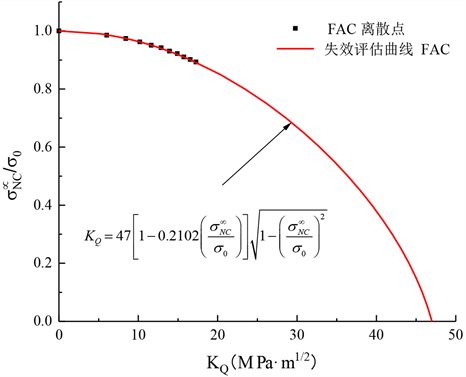
Figure 6. Failure assessment curve (FAC) obtained by fitting data points

图6. 拟合数据点得到失效评估曲线(FAC)

4.1. 失效评估点(FAP)

失效评估点即是对结构含裂纹焊接缺陷时，能否安全地继续工作进行评估。本文考虑焊接残余应力的影响，评价5A06铝合金带不同长度的中央裂纹缺陷板能否在给定载荷下安全工作。失效评估点需要确定两个参数，载荷比和总应力强度因子，载荷比通过式(7)计算，总应力强度因子通过式(8)计算 [28] 。

$\frac{{\sigma }_{NC}^{\infty }}{{\sigma }_0}=\frac{{\sigma }_{app}+{\sigma }_{res}}{{\sigma }_0}$ (7)

$K_{tot}=K_{app}+K_{res}$ (8)

其中： ${\sigma }_{app}$ 为施加的工作应力； ${\sigma }_{res}$ 为残余应力； $K_{app}$ 为工作应力下的应力强度因子； $K_{res}$ 为残余应力强度因子。

4.1.1. 残余应力的分布与K_res的计算方法

根据SINTAP规范 [30] ，对于平板焊接，纵向简化后的残余应力沿焊缝对称分布，简化后构件沿纵向的焊接残余应力分布如图7所示，其中 ${\sigma }_{yw}$ 表示材料屈服强度； ${\sigma }_{res}$ 表示焊接残余应力； $W_1$ 表示焊缝宽度； $y_0$ 表示残余应力沿纵向分布的尺寸：

根据图7的残余应力分布图，可计算直板存在不同长度的中央穿透型裂纹(图8所示)下的焊接残余应力强度因子 $K_{res}$ ，具体公式如下 [30] ：

令 $a=\frac{2c}{2}$ ， $b=\frac{W_1}{2}$ ；

当 $a\le b$ 时，

$K_{res}={\sigma }_{yw}\sqrt{\pi a}$ (9)

当 $b<a\le y_0$ 时，

$K_{res}={\sigma }_{yw}\sqrt{\pi a}\left(2/\pi \right)\left\{\left(2/\pi \right)-\frac{\left[{\left(a^2-b^2\right)}^{1/2}-b\pi /2+b{\sin }^{-1}\left(b/a\right)\right]}{\left(y_0-b\right)}\right\}$ (10)

当 $a>y_0$ 时，

$K_{res}={\sigma }_{yw}\sqrt{\pi a}\left(2/\pi \right)\left\{{\sin }^{-1}\left(b/a\right)-\frac{\left[{\left(a^2-b^2\right)}^{1/2}-{\left(a^2-b^2\right)}^{1/2}-b{\sin }^{-1}\left(y_0/a\right)+b{\sin }^{-1}\left(b/a\right)\right]}{\left(y_0-b\right)}\right\}$ (11)

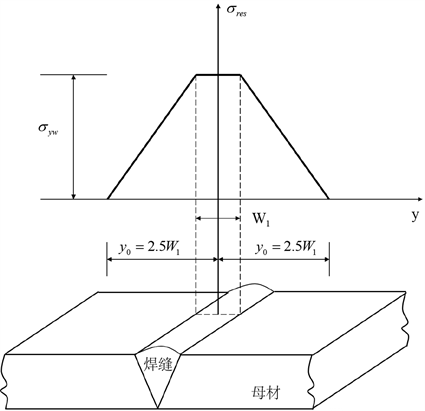
Figure 7. Longitudinal welding residual stress distribution diagram

图7.平板纵向的焊接残余应力分布图

4.1.2. K_app的计算方法

采用数值方法计算评估点裂纹应力强度因子 $K_{app}$ ，首先计算裂纹尖端的应力应变场，相应的有限元模型参见图3所示，对于断裂参数的计算方法选用精度可靠，且对有限元网格尺寸大小不敏感的虚拟裂纹闭合技术(VCCT) [31] [32] 。该方法假定裂纹扩展Δc引起的系统势能改变(减小)等于闭合裂纹至原来长度所作的功，其表达式如下：

$W=\frac{1}{2}{\displaystyle {\int }_0^{\Delta c}u\left(r\right)\sigma \left(r-\Delta c\right)dr}$ (12)

其中u是图10所示的相对位移，σ是应力，r是到裂纹前沿的距离，Δc指裂纹扩展的长度。因此，能量释放率G的表达式如(13)式：

$G=\underset{\Delta c\to o}{\lim }\frac{W}{\Delta c}=\underset{\Delta c\to o}{\lim }\frac{1}{2\Delta c}{\displaystyle {\int }_0^{\Delta c}u\left(r\right)\sigma \left(\Delta c-r\right)\text{d}r}$ (13)

要将图9中的裂纹闭合达到图10所示状态所需的功 $W=Fu/2$ ，其中 $F$ 是图10中 $i$ 的节点力，u是图10中 $i$ 和 $i^{\prime }$ 之间的距离。从而，我们可以根据方程(14)得到应力强度因子 $K_{app}$ 。

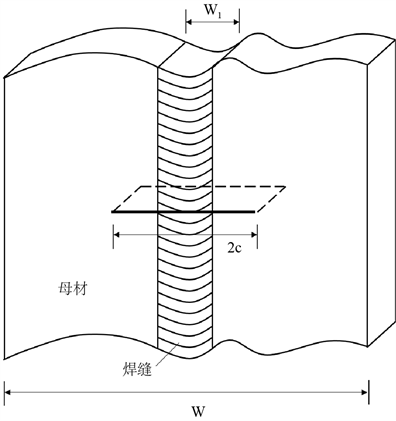
Figure 8. Diagrammatic sketch of a plate with a central crack defect

图8. 平板含中央裂纹缺陷示意图

Figure 9. Virtual crack closure model

图9. 虚拟裂纹闭合模型

$K_{app}\text{=}\sqrt{G\text{E}}$ (14)

式中：G为能量释放率，E为材料的弹性模量

4.1.3. 5A06铝合金板焊接残余应力分布与K_res的计算

已知5A06铝合金材料的屈服强度 ${\sigma }_{yw}$ 为175 MPa，焊缝宽度W₁ = 6 mm，利用图7可获得5A06铝合金材料残余应力场的分布(图11所示)，使用公式(9)，(10)和(11)可算得不同裂纹长度2c下的 $K_{res}$ ，并获得 $K_{res}$ 与裂纹长度c关系曲线(图13所示)。

4.1.4. 5A06铝合金板在不同工况下应力强度因子K_app的计算

采用有限元法计算了5A06铝合金板不同工作应力 ${\sigma }_{app}$ 作用下裂纹前沿的应力与应变场，再使用VCCT法计算裂纹前沿的应力强度因子 $K_{app}$ 。表4列出了不同裂纹长度，不同工作载荷下裂纹前沿应力强度因子。

Figure 10. The model of crack extension is Δc

图10. 裂纹扩展Δc的模型

Figure 11. Residual stress distribution of 5A06 aluminum alloy

图11. 5A06铝合金材料焊接残余应力分布示意图

4.2. 5A06铝合金含中央穿透型裂纹安全性评估(FAD)

利用SINTAP提供的焊接残余应力 ${\sigma }_{res}$ (图11所示)和对应焊接残余应力 ${\sigma }_{res}$ 的应力强度因子 $K_{res}$ (图12所示)，通过表4、式(7)和式(8)可计算得到评估点的参数(如表5和表6所示)，结合图6的失效评估曲线FAC，作出不同长度的穿透型裂纹的焊接平板的FAD如图13所示。

5. 结果与讨论

如图5所示，采用有限元计算和极限载荷分析方法得到的极限应力随着裂纹长度的增加而减小，获得了极限应力与裂纹尺寸的定量关系，采用该方法获得了5A06铝合金的FAC曲线，克服了由实验获得FAC存在的失效状态的检测困难，周期长，成本高，不便于应用等不足。残余应力的分布与焊缝的尺寸和屈服应力直接相关。如图12所示，在残余应力作用下应力强度因子随着裂纹长度的增加而先增加后减

Table 4. Stress intensity factors under different working conditions

表4. 不同工况下应力强度因子

Figure 12. The relationship between the residual stress intensity factor and the half crack length

图12. 残余应力强度因子随半裂纹长度c变化图

Table 5. Fracture parameters of 5A06 aluminum alloy with residual stress and working load (40 MPa)

表5. 残余应力和工作载荷(40 MPa)作用下5A06铝合金的断裂参数

Table 6. Fracture parameters of 5A06 aluminum alloy with residual stress and working load (80 MPa and 120 MPa)

表6. 残余应力和工作载荷(80 MPa和120 MPa)作用下5A06铝合金的断裂参数

Figure 13. Failure assessment diagram of 5A06 aluminum alloy

图13. 5A06铝合金的失效评估图(FAD)

小。故在焊接时应尽量减少焊缝宽度，减少残余应力影响范围，有利于焊接结构的安全。图13所示，当只有残余应力作用时，构件处于安全状态；当工作载荷达到80 MPa，构件的裂纹长度为12 mm时，构件处于临界状态；当工作载荷达到120 MPa，构件在给定的几种裂纹长度下均处于危险状态。残余应力的存在，对构件的安全性评估影响较大。故对结构进行安全评估时，考虑焊接残余应力是十分必要的。

致谢

感谢国家重点研发计划项目(No:2016YFB1102100)经费资助。

NOTES

$$

^*通讯作者。