1. 引言
据文献 [1] [2] 及有关文献中有关于宇宙红移的争议,文献 [1] 文中p. 244图8.46的7315颗类星体红移-视星等关系图,不服从哈勃定律。没有全红移-视星等哈勃图。所有文献中的光度距离都没有统一的方程。超新星延时方程
正确吗?星系当时发出的电磁波长
就是地球上接收的波长
吗?星系的光度分别有全部红移距离图?等等。特别是(下面所有引用文献)现在出现暗物质,暗能量两朵天文学物理学的乌云,无法解析!大部分都是现代学者提出标准宇宙学所存在的重大缺陷,据星系,类星体大量观测的数据,用下面导出新引力宇宙度规,分析验证前述问题后,结合Newton引力论和Einstein引力红移,部分综合分析星系质量计算,暗能量存在与否等问题,必须在考虑全宇宙物质引力效应后,得出新的解析。通过分析得出整体宇宙都是引力控制,黒洞内和宇宙的引力不是中心形,是均勻形的结论。星系质量计算通过Newton中心引力与宇宙均勻引力综合应用得出的。暗能量是纯宇宙均勻引力的应用。
文献中星系质量计算仅与引力定律有关,这还没有完全确定,争论多;现在用Schwarzschild 度规结合新引力宇宙度规初步计算星系质量,得出星系质量与文献中星系质量有较大差别,下文中计算的星系质量还是初步的,还有很多需要改进,其计算的方法不能忽略。在计算宇宙平均物质密度时,用经过大量星系观测的数据理论分析结果与标准宇宙学结果比较,作者系列文献仅用1个宇宙视界常量贯穿全部文章,计算的宇宙平均物质密度与文献计算的值接近;计算的可测物质与暗物质的比值与文献估算的值符合。
2. 基础方程的导出
据文献 [1] [2] 及有关文献中有宇宙红移争议,宇宙红移是否准定是Doppler红移?经长期分析狭义相对论的Doppler红移方程,结合引力定律可以得到星系与地球或太阳系的距离和宇宙红移的新方程,为经典距离。
,或
,
(1)
方程中,
是Schwarzschild非旋转黑洞半径。文献没有这样定义的距离,和开普勒行星运动3定律类似,由方程(1)推出的方程(3)可以互相验证,但不能从任何理论中推出这经典距离。对于宇宙而言是可观测宇宙的引力半径或宇宙视界半径。
,
是唯一待定常数,
是光速,
是经典距离,
是宇宙红移,G是引力恒量,
是黑洞或可观测宇宙质量。
对称法求出Schwarzschild黑洞的经典距离。
,或
,
(2)
方程(2)中
是引力红移,经检验适合于恆星表面的引力红移。Schwarzschild 推导他的度规时已隐函在其中。将方程(2)代入Schwarzschild 度规消去
便得到用
表述的度规,是Schwarzschild 度规现代化,把引力红移嵌进度规中。仔细分析Schwarzschild 度规,结合方程(1)可以得到不旋转黑洞内的度规,又适用于宇宙的度规,为新引力宇宙度规线元
(3)
方程(3)和Schwarzschild度规线元球对称,也是稳态度规。方程(3)为新宇宙学模型。
是Schwarzschild 度规线元和方程(3)的共同奇异性。方程(3)和Kerr度规球对称黑洞内的解都是爱因斯坦引力场方程的解,以上方程(3)的求解完全符合数学方程求解方法。 因此方程(3) 中的宇宙红移是引力红移不同表现,不同于人们熟知的Schwarzschild度规引力红移的数学表述。黑洞外是Newton引力中心势
,黑洞内或宇宙是由无限多个Newton引力中心任意放置,形成基本均匀的引力势
其数学表述恰好是Newton引力中心势的倒数,或者说黑洞内或宇宙引力势和Newton引力中心势球对称。方程(2)引力势与引力红移密切相关。方程(3)笫一个等号是经典度规线元,笫二个等号现代度规线元,后面的推导分别用经典或现代导出相同结论,统一用红移
表述。Schwarzschild度规也有上述情况。广义相对论既是经典理论,又是现代理论。方程(3)消除了
的引力奇性。方程(3)在宇宙任何点都适用。当代学者公认宇宙红移是Doppler红移,这里暂时定为宇宙红移是宇宙均匀的引力红移,读者必否定这种观念,请参阅文献后面4篇文章和下面的讨论是否可信,再作断言。或者说Einstein引力场方程的解方程(3)是引力解,能把宇宙红移嵌进方程(3)度规中,是判断宇宙红移为引力红移的条件之一。方程(3)是Einstein引力场方程的一个解,百年来人们求解Einstein引力场方程的解有几十个解,人们解不出方程(3),没有方程(1)就不知有方程(3)。如同没有开普勒行星运动3定律,Newton就不能推出引力定律相同。中科院理论物理所的玄论研究员李淼曾在科学网上(2008年)说,百年来人们创立百多种宇宙学模型,天文学家分析宇宙观测数据仍是唯象型,直到现在仍如上情况。现在就可以据方程(1)(3)理论分析宇宙观测数据,下面计算可观测宇宙球体积2个应用。
通过宇宙大范围观测事实,宇宙基本均匀分布,在方程(3)基础上,并受到宇宙物质引力效应
(这个因子星系观测的大部分物理量都必须用)减小观测星系数量,那么可观测宇宙体积
(4)
,若
是经典欧氏半径,欧氏体积
,比较前后体积有
。方程(4)中不考虑宇宙物质引力效应
时,计算出不旋转黑洞体积或可观测宇宙实际体积,
(4a)
其中
,不旋转黑洞体积或可观测宇宙实际体积是欧氏体积的3.2倍。还无文献类似用红移准确函数表述球体积,随红移增加对应不同球体积准确值,而且方程(4)(4a)互相叠在一起,分析宇宙物质分布能精确描述。表明球体积准确值不仅只有欧氏球体积。由于宇宙视界是有限值,不能无限大,当红移趋于无穷大时,方程(4)(4a)最大值,是人类观测球体积有限的最大值。欧氏半径可以无限大,其球体积可以无限大,但实际应用时是最小值。
Einstein引力场方程的解,必含有引力,如果解不含引力则解是错误的,百年对Einstein引力场方程求解,都存在这个缺点。同时引力的数学表述不仅是Newton中心引力表述,应该还有均匀的引力表述,正是Einstein引力场方程的精准内函。在1960年Kruskal用坐标变换消除Schwarzschild度规黑洞面奇性的新度规,人们称为Kruskal度规,并出现
Newton引力奇性,直到现在没有天文观测验证和理论分析应用于天文观测数据,亊实上Schwarzschild度规已消除Newton引力奇性
,Schwarzschild黑洞内恰是新引力宇宙度规,Schwarzschild度规黑洞面奇性不能消除,Einstein引力场方程本来自然存在的黑洞面奇性,经过大量理论分析星系观测数据验证新引力宇宙度规,才是Einstein引力场方程的正确理解。Schwarzschild 度规是中心引力度规。前者原点可以有无物质存在无关;后者原点必须在物体质量中心才有效。而且完全把宇宙红移能嵌进方程(3)度规中,引力红移方程(2)也能嵌进Schwarzschild度规中。这两个球对称度规,既可以用Einstein思路数学推导,又可以纯红移推导,结果完全相同,但文中无法分两种方法详述。
3. 星系质量新分析
计算天体质量的Newton引力中心方程是
(5)
方程(5)是教材常规方程。此方程对计算恆星质量很适合,计算星系和星系群(团)质量时,前述新引力宇宙度规的基本均匀分布引力效应,会产生强大的影响效应,或者说文献中计算星系和星系群(团)质量存在过剩。据教材知太阳离银心约8.5 kpc,绕银心速度约220 km/s,由方程(5)计算出银河系质量约是9.567 × 1010Mʘ。
宇宙视界是上世纪定出,约为
(1GІ·y = 109光年,1 Mpc = 106秒差距)(文献 [1] p69书中称为理论值,经验证置信度高,但不精确)。太阳质量是Mʘ = 1.989 × 1030 kg。假设
时,由方程(1)(2)推出,实为
, (6)
方程(6)表示星体引力中心势与宇宙均匀引力势等值条件,因此有
(7)
其中M为星体质量,
为星体中心距离与宇宙均匀引力效应的红移相等半径。把太阳质量和宇宙视界代入方程(7)计算出
,这个距离在柯伊伯星云和奥尓特星云之间,这里没有考虑银河系的引力红移效应。并计算出
处
。据方程(5)或(8)
处,绕太阳公转小行星的速度是
,公转周期T ≈ 35万年。宇宙均匀引力效应的宇宙红移对星系的引力红移又有何贡献?把方程(5)代入方程(7)消去质量M导得
(8)
方程中
速度单位是km/s,是恆星绕星系中心公转速度。
是星系中心到速度
的距离,星系引力红移与宇宙红移相等半径,简称引力双红移半径。为了检验上述方程的正确性,复制文献 [2] 中下列2图分析。如果盲目从两图中找出
和
十分麻烦,仔细分析后,可以用方程(8)直接在下面两图中绘出其拋物线正值曲线,这拋物线对称轴正是横轴,拋物线和星系自转曲线必交于一点,这交点坐标即是
,因两图是唯象图,放大图分析交点坐标时,原图作者绘图不精确,这交点坐标也不精确,但不影响理论分析的置信度(下面图1中没有绘拋物线,在图2的黑点上即(5.457 kpc,200 km/s)处)。
据两图1,图2及文献 [3] - [8] 图中点坐标
结合方程(8)得出表1的2,3列数据,再用2,3列值用方程(5)计算出点坐标
处的星系质量,最后用这星系质量据方程(1)(2)计算出第5列星系中心引力红移和宇宙红移相等值。银河系自转曲线图1,图3和文献 [4] 图A1 (附录1)图的曲线所得值相近,椐文献 [6] 图A2(附录1)银河系自转曲线值较大一些,故另一行值。
为了对表1的深入了解,任选3个星系点坐标
两旁从上面图中曲线量出
列表2,表2中每个星系3行值中间行是表1对应值,上下两行是点坐标
计算所得值。用2、3列值由方程(5)计算星系在该点的质量,为第4列,4列值用方程(7)计算出第5列,3、4列值用方程(2)计算出第6列,2列值用

Figure 1. Distribution model of mass of galaxy. The general curve used in the article is Figure 8.16 of Literature [2]
图1. 银河系质量分布模型,文中计算用总体曲线,是文献 [2] 的图8.16
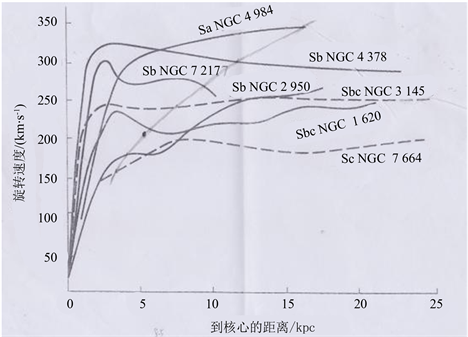
Figure 2. Flat part of seven rotation curves of vortex galaxy stretches from the center to a very far place. It’s Figure 9.17 of Literature [2] . The curve crossing the rotation curve in the Figure is parabola of Equation (8). The dark sport is the intersection of galaxy curves
图2. 7个旋渦星系的自转曲线,平直部分从中心伸展到很远距离。是文献 [2] 的图9.17,图中交自转曲线的曲线是方程(8)拋物线,拋物线上黑点是银河系曲线交点
方程(1)计算出第7列。
现在讨论表2中星系ScNGC7664的情况,点坐标
是中间值,点坐标
在中间值右边(3.98 kpc,165 km/s) (值大),MG = 2.520 × 1010Mʘ (值大),
(值小),说明星系引力中心势与宇宙均匀引力势等值,或引力红移与宇宙红移等值。距离
,并有
,在r处证明星系引力中心势小于宇宙均匀引力势,或者说r处星系引力中心小于宇宙均匀引力。反之星系Sc NGC7664第3行情况有
,
,在r处证明星系引力中心势大于宇宙均匀引力势,或者说r处星系引力中心大于宇宙均匀引力。则点坐标
是星系引力中心等于宇宙均匀引力处。其余旋渦星系引力情况分析相同。
文献 [9] 图3左图中作者在太阳处绘出方程(5)的开普勒运动曲线(虚线),
情况在
(这个值恰在文献 [10] (沈俊太) P. 198图3-1-1(a)中银河系核球)处完全符合,其余点不成立,方程(5)对行星公转正确。银河系的
值恰好在核球处,那么其余星系的
值是否恰好在核球处?还没有资料可查对。据上面分析星系计算质量时,方程(5)必须考虑宇宙均匀引力势效应。据下列文献教材知太阳离银心距离约8.5 kpc,前面计算出银河系质量是
。把8.5 kpc代入方程(8)计算出v ≈ 249.6 km/s,由方程(5)计算银河系质量
。比较二个银河系质量,都不是8.5 kpc內的银河系确定性质量。银河系大于
处,观测的自转速度值及r值据方程(5)计算出银河系不确定信的质量。因为宇宙均匀引力大于Newton中心引力,从5.457 kpc到晕外边界的银河系的质量是逐渐稀簿,其自转速度没有象行星公转速度随
而减小,如Sb NGC2950,Sc NGC7664,Sa NGC4984等,自转速度增加,减少很小自转速度如银河系,M31,Sa NGC4378,NGC6286等。椭圆星系也有相同情况。显然方程(5)不能计算大于
的星系质量。点坐标
计算星系内部分质量,相当于太阳在该点计算质量相同。可将点坐标
用方程(5)计算星系质量等同于恆星质量计算。文献 [2] 表9.6银河系质量约是4 × 1011Mʘ,实际是文献 [11] p63给出
,晕外边界
,据方程(5)计算出银河系前述质量。文献 [11] P. 10表1.2银河系盘质量约6 × 1010Mʘ。下列文献教材还有银河系更大质量约

Table 1. Mass of point of galaxy and z U = z n are figured with 21 vortex galaxies and 8 point coordinates of elliptical galaxy ( r U z n , v )
表1. 21个旋渦星系和8个椭圆星系点坐标
计算出星系该点质量及
表1中右上角[*]数字是文献序号,其中文献 [3] - [8] 的图没有复制在文中。
In Table 1, the numbers in [*] at the top-right corner are the sequence numbers of literature. And figures of Literature [3] - [8] aren’t copied in this article.
2 × 1012Mʘ。可知计算银河系质量很混乱,没有统一的太约值。现在恆星质量计算值比较统一,百年多星系质量没有统一的太约值。原因是标准宇宙学理论无法给出计算星系质量的方程,Newton引力中心理论任意扩大应用所致。这是广义相对论推扩至全宇宙时,经过理论验证,才知上述情况。
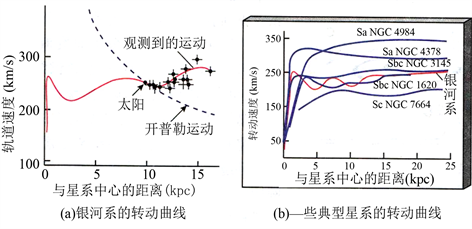
Figure 3. Black spots of Figure 6.10 and Figure 2 in Literature [9] are on the rotation curve (red curve) of galaxy on the right figure above. Dark spots on the parabola in Figure 2 are on the red curve of Figure (b)
图3. 文献 [9] 的图6.10,图2中黑点是上面右图银河系自转曲线(红线)上,图2中拋物线上黑点在(b)图大致在红线上

Table 2. There is the comparison of point coordinates ( r U z n , v ) and ( r , v ) of three vortex galaxies, which explains the existence of point coordinate ( r U z n , v )
表2. 3个旋渦星系点坐标
和
有关值的比较,说明点坐标
存在性
从上面分析可知:
1) 由表1知,似银河系减少很小自转速度的星系在小于
的质量是总质量的50%以上,那么银河系总质量约是1~1.2 × 1011Mʘ,或多一些。据此推知M31的总质量约2.6 × 1011Mʘ。
文献 [2] 表9.6这两个星系总质量分别约4 × 1011Mʘ (上世纪计算值),银河系不可能有2 × 1012Mʘ那么大。由此可知M31大于银河系总质量1倍多。史匹哲太空望远镜在2006年重新估计银河系的质量大约是仙女座星系的50%,M31大约是7.1 × 1011Mʘ (这个值还是超大,维基百科)。此处理论分析银河系的质量大约是仙女座星系的50%,符合直测结论,那么前面的计算是合理的。则NGC6286总质量约1.6 × 1011Mʘ (文献 [8] 以v = 240 km/s,r = 8 kpc,计算出NGC6286质量约1.1 × 1011Mʘ,作者估计总质量约2 × 1011Mʘ)。文献 [12] 表1(英2015年7月),作者改造方程(5)得星系盘质量新方程
,计算出有5个星系质量与本文表1相同星系质量列表3比较。
据文献图和表1结合估计值,原文
对数值已化成具体值,比较知
值比以前文献更接近真实星系质量,
值小些,有其合理的分析。如见表3。

Table 3. Comparison of two equations of calculating galaxy’s mass
表3. 2种方程计算星系质量的比较
2) 从图2看出星系Sb NGC2950在表1中点(4.131 kpc,174 km/s)内质量约2.908 × 1010Mʘ (用方程(5)计算出),图2该星系自转曲线上至速度250 km/s以上,离星系中心20 kpc以上,那么大于4.131 kpc以上质量约是前述质量的1~2倍,那么这星系总质量约6~9 × 1010Mʘ。可推知星系Sc NGC7664总质量约7 × 1010Mʘ。
3) 表1中星系Sa NGC4984在
内的质量约4.5998 × 1011Mʘ,可以估计其总质量约是1012Mʘ(是前计算质量约2倍以上估算),故表1中其余星系总质量都小于1012Mʘ。星系
的质量计算还没有统一规范,只能估算1~3倍。所以上述星系总质量上述方法估算出的。
由上3点分析星系总质量是大致估计值,因为
星系质量必须考虑Newton引力中心和宇宙基本均匀的引力综合效应,所以方程(5)不能在
星系质量计算。可知现有文献用方程(5)计算星系总质量过大,估计实际星系总质量是文献用方程(5)计算的十分之一左右,是人们难于接受的结论,怎样计算?待进一步研究,计算的星系总质量更合理。上述的计算不可忽略的。
上面星系自转曲线与方程(8)交点
的情况分析,矮星系自转曲线与方程(8)交点还没有讨论。假设用现在的宇宙视界138.233亿Ⅰ.y = 1.3078 × 1026 m,那么方程(8)的常量改变后为
(8a)
可适用于矮星系上述讨论,不适用于前面的分析,此处不详讨论。
文献 [11] P. 37有牛顿第三定理:同形体作用于其内腔中任何一质量的引力势之和为零。上面分析可知,黑洞内和整体宇宙牛顿第三定理不成立。
4. 宇宙物质密度新计算和应用
4.1. 宇宙物质密度新计算
经上面讨论知,宇宙视界在新引力宇宙度规应用中可信度高,现在用来计算宇宙物质密度和可观测星系的数量。由
和
(其中
,
分别是宇宙局域观测总质量和宇宙物质密度)导出
(9)
这个宇宙物质密度值比文献 [9] p268的值
小,比文献 [13] [14] 的值
更小。文献 [1] 附表2的值是
。据教材给出R-W度规体积
,任何文献没有应用这个值,且各位作者们计算宇宙物质密度仍用欧氏体积计算上述文献的值。宇宙物质密度无法统一,量级相同。宇宙局域总质量是(宇宙视界值前面给出)
(10)
将方程(9)代入
中计算可观测宇宙局域引力效应总质量(前者缺引力效应)。
个星系 (11)
以每个星系质量约1011Mʘ估算。方程(11)的值符合各文献的值。可知
,恰好是方程(4a)(4) (
)比值。或者说可测的宇宙质量是宇宙局域总质量的1/7 » 14.3%,不可测宇宙质量1/7 » 85.7%,文献 [10] P. 6 (吳岳良,周宇峰)第2段:大部分暗物质约占85%,可测物质约占15%,广义相对论推出的新结论与现有推测完美符合。方程(4)最后等式的恆量不计有
,据很多星系,类星体表统计知
红移数量都小于总量的10% (这个结论是经过统计得出,经得起检验的结论)。再对方程(4)的
不积分,便是的宇宙红移概率曲线方程
(12)
这概率曲线的极大点(0.847,0.5756),图4中点曲线,比较文献 [15] 中(P. 74的Figure 3.15,图在附录2的图A3)的图中(唯象图)的对应红移值略大-些,极大值小很多,类似性很强。教材中说
星系观测数量下降,方程(12)符合观测亊实(注:这概率曲线与视星等无关)。以上分析知方程(4a)计算宇宙物质密度和局域物质总量,方程(4)计算可测物质量并得到观测数据的验证。在
时,有
。如果从宇宙中任一点任意方向以光速运动的观测者,观测者在运动轨迹任意点测的空间球体是
,
(不是初始点球体,这2个值是恆量)。同时他只能测出对应的
,
(对应
,
的恆量),但是
产生的引力效应又控制观测者运行轨迹(是空间类螺线)和距离,观测者永远不能离开初始点
这个空间球体。或者说
的物质永远不可测的量,故现有文献说的暗物质是没有办法可测!图4中下面第1条可测质量曲线据方程(4)是
,上面不可测质量曲线据方程(4a)是
,中间虚线是不可测质量曲线
。点线是概率曲线
。如见图4。
4.2. 宇宙新物质密度应用
为了加深上面结论理解,再对方程(4a) (4)和欧氏体积作具体例子计算分析。当
(这时方程(1)计算出
)时,前述2种黎氏体积和欧氏体积近似相等,假设以这半径银河系为中心的球体,约有3 × 1016Mʘ时,都能计算出这个球体内物质密度大于
。一般
时,前述3种体积都近似相等,物质密度定值时,计算3种体积內质量也近似相等。当
时,3种体积內质量逐渐产生巨大差别。
离银河系的
大约小于0.009时,方程(4a) (4)不适用,这时正处于星系构成的长城內,物质密度大于宇宙物质平均密度千倍以上。
时,方程(4a) (4)计算体积內质量近似相等。当
时,方程(4a)(4)计算体积內质量逐渐产生巨大差别。以方程(9)值计算方程(4a) (4)时,当
时,其中
,
,
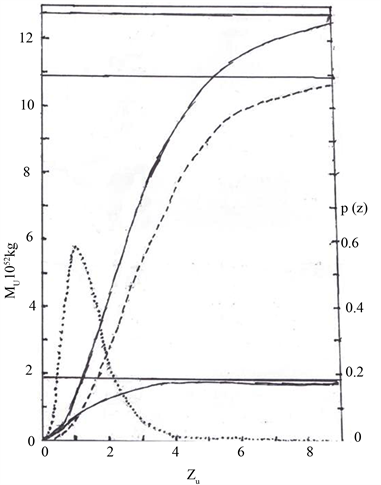
Figure 4. Full curve below is
, dotted curve in the middle is
, full curve above is
. The three parallel lines are asymptotes of the three mass curves and the ratio is 1.8204:10.923:12.743 = 1:6:7. Dotted line is probability curve
.The vertical axis on the left is
and the vertical axis on the right is
. The abscissa axis is redshift. The four curves are perfect, smooth and accurate theoretical curve controlled by homogeneous cosmic gravity
图4. 下面实曲线是
,中间虚曲线是
,上面实曲线是
,3条平行线是3条质量曲线的渐近线 比值是1.8204:10.923:12.743 = 1:6:7。点线是概率曲线
。左边纵轴是
,右边纵轴是
,横轴是宇宙红移。4条曲线都是宇宙均匀引力控制的完美平滑精确理论曲线
则
。
若现在可观测的
时,同法计算,由方程(4a)(4)计算体积內质量
,
,接近6倍。据上世纪80年代文献较少提及暗物质,上世纪90年代文献逐渐提及暗物质,现在对暗物质才加强认知,是宇宙红移观测逐渐到9以上,理论分析时出现的困境产生的。以上分析可知在很小红移时,可以观测98%以上的星系红移,随星系红移值逐渐増加,比较暗的星系或矮星系,如本星系群中矮星系占一半多的IC10,Leo І,Leo A等等,随红移增大会逐渐观测不到,暗物质来源是其中主要原因之一。前面§2星系自转曲线和晕中质量的计算也是暗物质来源次要原因。这2种观测不到星系,星系计算质量超大,星系之间的物质流,星系构成的长城之间巨大空洞内更稀簿物质密度小于
,也是观测不到的物质。这些物质之所以观测不到,是受到宇宙基本均匀极稀簿物质产生极微弱引力累积贡献,电磁波在宇宙中长距离传播受极微弱引力累积最强大的基本均勻效应(参考§1末段)。
上面分析既简单又十分抽象,经理论分析大量宇宙观测数据(不是全部),如果没有理论分析大量星系观测数据,则上述结论是空中楼阁。
以此而言当今观测的宇宙巨大空洞内不能是真空,其空间必存在不可测的质量,物质密度可能小于
(近似于1个光子质量,文献 [1] P. 291),现在还是一个谜。星系构成的长城集群中宇宙质量较多的区域,物质密度可能大于
。新引力宇宙度规看到宇宙有限,这度规适用于宇宙任何一点,故宇宙无限,方程(9)物质密度值可推扩到无限宇宙中。这种宇宙观念完全违背当代主流大爆炸宇宙有限观,但是符合Einstein,Bondi,Gold,Hoyle上世纪50年代前的稳常态无限宇宙,但有本质的区别。据Einstein推导出星体引力中心红移值后,并得到观测和实验的验证。因此,虽然宇宙物质密度
极小,这么小的质量在1 m处引力红移,据Einstein推导
,是极微弱引力中心红移贡献(当代没有人这样考虑,现在必须这样考虑)。当星系发射出电磁波在宇宙中长距离传播过程
极微弱引力中心红移对长距离传播过程的电磁波产生强大的效应,这
引力中心红移贡献累积效应就是宇宙红移
。据方程(1)和Einstein推导,可计算在任意点离1 m处的宇宙红移
,比较
和
大于27个数量级,是
的
叠加成宇宙红移。故宇宙和黑洞内的基本均匀引力势是方程(1),当代公认的宇宙“暗能量”是宇宙基本均匀极微弱引力效应,不能有数量表述(文献 [10] P. 135 (张鹏杰):暗能量是宇宙学常数吗?),是方程(3)的度规表述。
众所周知,整数可分为奇数和偶数,这3种数对应一样多。从图4知,计算出
与
的体积和质量,前者小于后者,后者物质密度是均匀分布体积大,前者物质密度是宇宙红移增加逐渐稀簿体积小。实际上前者的体积和质量都分布在后者整体。由方程(4) (4a)及(9)可以推出,红移
的
球壳层处可观测物质密度(注意
球壳层的物质密度不变,散布在对应
球壳层处物质密度是变量,即
,
(13)
可计算出
,
,
,
值,这4个值清楚看出红移
的
球壳层处可观测物质密度随红移增加而减小。而
和
的各球体物质密度
是不变量,此情况符合宇宙观测亊实,并能精确分析可观测物质密度随红移变化规律。方程(13)的分子值是
球壳层处可观测物质的数量。计算式子繁,介绍计算过程如下:方程(13)分子
,分子小括内用方程(4)计算可观测宇宙
球壳层体积,对
计算式如下
。
分母观测实体宇宙
球壳层体积,用方程(4a)计算,
。
将上述数据代入方程(13)便是
值。余下同法计算。
上面方程(13)计算说明宇宙
球壳层处可观测物质密度随红移增加而减小,正如附录3复制图A4是文献 [16] 的星系、类星体扇形二维红移平面图,星系、类星体点分布随红移增加而由密变稀疏。用可观测物质密度随红移增加而减小解析星系、类星体点分布随红移增加而由密变稀疏的分析是恰当的,密度数值也接近实际,文献还没有类似的解析。理解较抽象。
5. 讨论和结论
综合以上分析。1) 新引力宇宙度规确是Schwarzschild度规球对称解,即是Einstein引力场方程的解,比任何Einstein引力场方程的解更简单,分析应用跟Newton引力定律那么简洁普适。如果标准宇宙学是普适的准确理论,学者们为什么创造出百多种宇宙学模型(Newton引力中心定律已击败许多不同引力论),如文献 [1] 及王永久的《引力论&宇宙论》中介绍很多种宇宙学模型,但都没有精确地理论分析星系观测各种物理量?王永久的文中介绍142个类似Einstein推导的结果,几十年来看不到天文观测验证的公布。2) 新引力宇宙度规导出的体积方程(4) (4a),在黎曼几何中没有用红移表述准确的体积计算(读者若知黎曼几何教材有此表述请指正),这体积在分析宇宙物质密度和可观测星系的数量符合直测事实外,用于星系的宇宙红移数量分布分析符合观测数据等。文献无这样的讨论。新引力宇宙度没有宇宙年龄可分,只涉及星体和星系年龄分析。3) Newton引力中心定律结合宇宙均勻引力可知星系质量的计算只是现有文献值的十分之一左右,并从直测和理论讨论得知银河系质量大约是M31的50%,且银河系的
值恰好在核球处,验证理论和直测令人惊奇的符合,文献没有这方面的验证。因此星系晕中的“暗物质”没有文献中计算的那么多。这一点带给人们极大的疑问,怀疑上述推导是否合理,但不是最后的结论,已在超
星系质量计算上待进一步研究。这样的分析又不能全否定无用,有其合理的分析。宇宙中很多矮星系随宇宙红移逐渐增加而看不见,稀簿的星系际尘埃直测不到等等都属于不可测物质—暗物质。是宇宙均勻引力效应。不可测物质和可测物质分布规律,前面讨论简洁清楚。据文献 [10] (吳岳良、周宇峰),暗物质约占85%,可测物质约占15%。上面理论分析暗物质是可测物质6倍,理论与估算应是互相符合。文献看不到不可测物质和可测物质详细分析分布规律。4) 宇宙“暗能量”是宇宙基本均勻稀簿物质的极弱引力效应,星系发射的电磁波在宇宙中长距离传播时,被极弱引力累积效应的贡献,具体表现为宇宙红移。5).可推知广义相对论可推扩至全宇宙,引力论不能只有Newton引力中心定律—Schwarzschild和Kerr度规,还有广义相对论的均勻引力定律—新引力宇宙度规和Kerr度规球对称度规(另文介绍)。6) 此处分析时只用1个宇宙视界恆量(是宇宙物质密度和引力恆量G的函数),且是学者们早已定出,分析星系观测数据很精确。而标准宇宙学,需6个以上的参量(文献 [10] (陈学雷) P. 22),计算出的值,难得观测的精确验证。文献 [10] P. 135 (张鹏杰):在宇宙学尺度上,广义相对论成立吗?以上验证广义相对论成立!上述的理论分析比任何文献更精确地接近星系观测各种物理量。文献 [10] 中指出Schwarzschild度规黑洞天文观测不到,称为数学黑洞,事实上全宇宙任何点看到的一个对应Schwarzschild度规内部黑洞,一个个这样的Schwarzschild度规内部黑洞叠加成无限宇宙。而R-W度规没法将宇宙红移嵌进度规中。据(Asger G. Gasanalizad 阿塞拜疆http://arxiv.org/1009.4775)文献 [17] 中末表3计算出哈勃望远镜数据较小于宇宙视界4.3 × 1027 m,根本不适用于方程(8),计算出星系质量或透镜星系质量比以前文献更大,且该作者没有应用于任何星系观测数据的检验。综合大量星系各段电磁波光度计算,透镜星系质量,星系质量计算比较得出宇宙视界约是6~6.2 Gpc,相当精确了。7) 近400年引力论的创立发展史知,只有Newton和Einstein在创立发展引力论后,用自己的理论直接分析宇宙观测数据并得出精确验证!而Fricdmann,Robertson,Walker (注:3位创立理论后,他们没有给出理论分析验证)没有像Newton和Einstein后续工作的成果验证!如果标准宇宙学已经似Newton和Einstein理论具有普适性和严密性时,方程(3)若不正确?!就不存在文献 [18] [19] [20] [21] 等及以上分析,层层递进,环环相扣,用引力思想接续了Newton和Einstein的工作。8) 当代所列文献有关前沿性的困难将会大部分得以解决,体现黎曼几何-广义相对论在宇宙观测数据理论分析的最广泛,最简洁精确的应用。此处不能一一列出。
附录1

Figure A1. Is copy of Galaxy’s rotation curves figure in Literature [4] and Literature [8] . After comparing, we can know that values of
of Figure A1 and Figure 1 are the same, and value of
in Figure A2 is greater
图A1. 复制文献 [4] [8] 银河系自转曲线图, 比较图1可知,图A1和图1基本同
值,图A2
值较大
图A1取自文献 [4] 的图7, CO-based rotation curve of the Galaxy, with Clemens (1985) data corrected for R0 = 7.5 kpc and V0 =190 kms−1. The curve is fitted by the expression V = 228 exp(−r/50 − (3.6/r)2) +350 exp(−r/3.25 − 0.1/r)

Figure A2. The Figure 10 of the Literature [8]
图A2. 文献 [8] 的 Figure 10
Above: The rotational speeds of tracer gases in the Galaxy (Milky Way Sb spiral). Measured data from [13] shown in curve 1. Theoretical curve from the Carmelian equation (15) (curve 2) and from the Newtonian equation (8) (curve 3)
附录2

Figure A3. The copy of Figure 3.15 in Literature [15] . It’s probability figure of i apparent magnitude, which has high similarity with Equation (12)
图A3. 复制文献 [15] 图3.15i视星等概率图,与方程(12)类似性很强
The Figure 3.15 of Literature [15] shows the redshift probability distributions for faint galaxies. The dashed curve shows a best fit to the measured and debiased DEEP2 redshift distribution for galaxies with i < 23, and extrapolated to i < 25 (see text).The other two curves show model predictions for galaxies with i < 25 (magenta: the Millennium Simulation; green: an evolving luminosity function; see Figure 3.14).
附录3
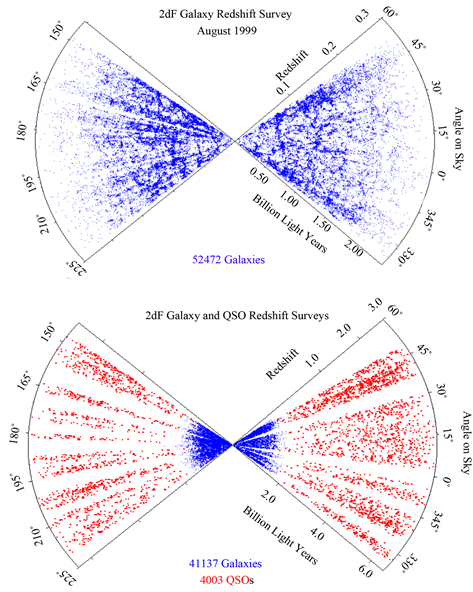
Figure A4. Is the copy of Figure 2 in Literature [17] . It’s the two-dimen- sional figure of redshift’s distribution of galaxy and quasar, which is in accord with the distributing rule of Equation (12) and Equation (13). Quantity of point coordinate decreases as redshift increases, due to that density of observed matter decreases as redshift increases
图A4. 复制文献 [17] 图2。是星系、类星体的红移两维平面分布图,符合方程(12) (13)的分布规律。点坐标随红移增加由密变稀,是观测物质密度随红移增加逐渐减小成形
We can see from this picture, redshift cone diagram showing the distribution of objects from the 2dF galaxy and QSO redshift surveys as of August 1999. The top panel shows the distribution of the galaxies alone, and the bottom panel shows the distributions of both galaxies and QSOs.