时频分析方法：研究与展望

Time-Frequency Analysis Method: Research and Prospect

摘要: 时频分析联合时间频率表示一维时间信号，是非稳态信号处理的重要工具之一。本文综述了时频分析方法的研究进展，在此基础上阐述了各种时频分析方法的原理及其优缺点。通过数值模拟试验，比较了各种时频分析方法的频谱表示特征。最后，对时频分析方法进行了展望。

Abstract: Time-frequency analysis method represents one-dimensional time signal into time and frequency domains, which is an important tool for non-stationary signal analysis. In this paper, the time-frequency analysis methods were reviewed; furthermore, a survey of the principles, the ad-vantages and disadvantages of various time-frequency methods were given. Numerical simulations were carried out for comparisons. Finally, a short prospection about time-frequency analysis was given in this paper.

1. 引言

时频分析研究非平稳信号频谱随时间的变化规律，该方法将一维时间信号分解到时间频率域。如何准确刻画非平稳信号的频谱变化规律一直是人们关注的问题之一 [1] 。近几十年来，时频分析方法有了很大的进展，并成功应用于地球物理 [2] [3] 、环境科学、地质学等领域。常规的时频分析方法大致可以归为线性方法和二次变换两大类。如短时傅里叶变换 [4] (Short-time Fourier Transform, STFT)、连续小波变换 [5] (Continuous Wavelet Transform, CWT)和S变换 [6] (Stockwell Transform, ST)为线性时频分析方法。Wigner-Ville变换 [7] [8] (Wigner-Ville Distribution, WVD)及其衍生的核函数光滑法 [9] [10] [11] 为二次时频分析方法。近些年发展起来的时频分析法主要有基追踪 [12] (Basis Pursuit, BP)、Kalman滤波方法 [13] 、经验模态分解 [14] (Empirical Mode Decomposition, EMD)、压缩小波变换 [15] (Synchrosqueezed Wavelet Transforms, SSWT)等等。

窗口傅里叶变换、连续小波变换和S变换利用窗函数对信号截断进行频谱分析。信号的频谱为信号与核函数的线性相关，不同的方法对应不同窗函数选取法 [1] 。线性时频分析方法具有易于实现的优点，但加窗会带来频谱拖尾等问题。另外，Heisenberg不确定原理揭示了提高时间分辨率是以牺牲频域聚焦为代价的，反之亦然 [16] [17] 。为提高时频分析的精度，Huang等提出了经验模态分解 [14] 。该方法是一种完备的、直接的、后验性的时频分析法，有很好的自适应性，但该方法会产生模态混叠现象。为了消除模态混叠现象，Torres等提出了集合经验模态分解 [18] (Ensemble Empirical Mode Decomposition, EEMD)。该方法是一种噪声辅助数据分析法，具有有效的抗混分解能力。但其分解不再完备，且计算成本高。鉴于以上结论，Torres等人又提出了完备集合经验模态分解 [19] (Complete Ensemble Empirical Mode Decomposition, CEEMD)。该方法在解决了完备性问题的同时，提高了信号的频谱分辨率，但该方法也没有完全解决模态混叠问题。Daubechie等提出的SWT方法 [15] 与EMD具有相近的时频分辨率，其严格的数学证明及其可重构性的优势使其在非平稳信号领域取得了重要的应用。Auger等指出压缩小波变换实质上是一种能量重排的时频分析方法 [20] 。基追踪 [12] 与匹配追踪 [21] 是将信号在字典库中进行分解，它们力图从符合信号特征的过完备原子字典中找到信号的稀疏表示。MP是一种贪婪算法，通过寻找字典原子与信号的最大相关来确定信号分量，通常找到的是次优解，而不是最优解。BP方法通过引入l₁范数，将信号的稀疏表示化为一类有约束的优化问题，进而转化为线性规划问题来求解。该方法由于要在所有的字典向量中极小化一个全局目标函数，其计算量仍然是很大的。短时自回归方法 [22] (Short-Time Autoregressive Method, STAR)相对于其它方法能捕获快速的幅度震荡，但其频率分辨率易受信噪比和自回归阶数的影响，谱图中可能会出现谱峰不明显、假峰、谱线分裂的现象。Kalman滤波方法 [23] 引入信号与噪声的状态空间模型，利用前一刻的估计值和现时刻的观测值来更新对现时刻状态变量的估计。这种方法的公式很简单，结果较精确，但由于算法本身的复杂性以及它对计算处理器的高质量要求，Kalman滤波方法的应用范围并不是很广泛。

时频分析是非平稳信号分析的重要工具之一，它可以帮助人们理解信号的复杂结构，揭示其内在规律。无论是常规方法还是非常规方法，它们的理论基础都是建立在各自的假设之上，没有一个通用的，绝对好的方法。我们要做的工作是：针对信号具体特性，选择合适的时频分析方法，进而更好的揭示信号的频谱随时间的变化规律。提高信号的时频分辨率是一个永恒的主题，近些年不断涌现的新方法，在提高时频分析精度的同时，使人们更好的认识时频分析。本文将分别阐述以上方法的基本原理，并结合实际例子对比分析这些方法的优势和不足之处。

2. 线性时频分析方法

短时傅立叶变换也称窗口傅里叶变换 [24] ，它是由Gabor首先系统使用的。该方法利用窗函数把信号分解成一系列“小片段”。每个“小片段”近似平稳，对每个“小片段”进行傅里叶变换得到信号的频谱。连续函数的STFT表达式为：

$S_F\left(\tau ,f\right)={\displaystyle {\int }_{-\infty }^{+\infty }s\left(t\right)w\left(t-\tau \right){\text{e}}^{-i2\text{π}ft}\text{d}t}$ (1)

其中， $w\left(t\right)$ 是窗函数，STFT也可表示为： $\langle s\left(t\right)\ast w\left(t\right),{\text{e}}^{i2\text{π}ft}\rangle$ 。

窗口傅立叶变换的窗函数是固定不变的，为了增加频谱分析的自适应性，Morlet等人提出了CWT [5] 。CWT是一种可变时窗尺度的线性变换，其分析窗由平移、伸缩后的母小波函数形成。因此CWT具有可

变的时频分辨率和较好的能量聚焦性。在小波函数能量单位化即 ${\displaystyle {\int }_{-\infty }^{+\infty }{\left|{\phi }_{a,\tau }\left(t\right)\right|}^2\text{d}t}={\displaystyle {\int }_{-\infty }^{+\infty }{\left|\phi \left(t\right)\right|}^2\text{d}t}=1$ ，和CWT约束条件即 $C_{\Psi }=2\text{π}{\displaystyle {\int }_0^{+\infty }{\left|\omega \right|}^{-1}{\left|\hat{\Psi }\left(\omega \right)\right|}^2\text{d}\omega }<\infty$ 的前提下，CWT的表达式为：

$W_s\left(a,\tau \right)=\frac{1}{\sqrt{a}}{\displaystyle {\int }_{-\infty }^{+\infty }s\left(t\right){\Psi }^{*}\left(\frac{t-\tau }{a}\right)\text{d}t}$ (2)

其中， ${\Psi }_{a,\tau }\left(t\right)=\frac{1}{\sqrt{a}}\Psi \left(\frac{t-\tau }{a}\right)$ 是母小波函数 $\Psi \left(t\right)$ 经过伸缩平移变换得到的。

小波变换将时间信号分解到时间尺度域，不是时间频率域。一个尺度代表了一个频带。

Stockwell等提出的S变换 [6] ，兼具窗口傅立叶变换和小波变换的优势，具有无损可逆性的特点。其表达式为：

$S_{ST}\left(\tau ,f\right)=\frac{\left|f\right|}{k\sqrt{2\text{π}}}\times {\displaystyle {\int }_{-\infty }^{+\infty }s\left(t\right){\text{e}}^{-\frac{{\left(t-\tau \right)}^2{f}^2}{2k^2}}{\text{e}}^{-i2\text{π}ft}\text{d}t}$ (3)

其中，参数 $k$ 由高斯窗 $\hat{\omega }\left(t,f\right)=\frac{\left|f\right|}{k\sqrt{2\text{π}}}{\text{e}}^{-\frac{t^2{f}^2}{2k^2}}$ 的宽度决定。与(1)和(2)作对比，ST可看作窗口函数为 $\hat{\omega }\left(t,f\right)$

的STFT，或者是与频率有关的变尺度的CWT。

我们选用由两个调频分量合成的信号进行分析，得到如下结果：图1为STFT得到的频谱图；图2和图3分别为CWT和ST得到的频谱图。从图中可以看出，STFT变换的窗函数是固定的，信号的能量均匀分布在“脊”线的周围。CWT和ST中窗函数的形状随着时间与频率的变化而变化。在低频，窗函数较为“矮长”，具有较高的频率分辨力；在高频，窗函数较为“瘦高”，具有较高的时间分辨力。

3. 二次时频分析方法

Wigner-Ville (WVD)分布是二次时频方法。它不涉及窗函数，不受海森堡测不准原理 [17] 的制约，因此，具有高的时频分辨率。其定义如下：

Figure 1. The STFT spectrum of the synthetic signal

图1. 合成信号的STFT频谱

Figure 2. The scalogram of the synthetic signal

图2. 合成信号的CWT频谱

${\text{WVD}}_x\left(t,f\right)={\displaystyle {\int }_{-\infty }^{+\infty }x\left(t+\frac{\tau }{2}\right)\times x^{*}\left(t-\frac{\tau }{2}\right)\exp \left(-j2\text{π}f\tau \right)\text{d}\tau }$ (4)

多分量信号的WVD不等于每个分量的WVD和。例如信号 $x\left(t\right)=x_1\left(t\right)+x_2\left(t\right)$ 的WVD为

${\text{WVD}}_x\left(t,f\right)={\text{WVD}}_{x_1}\left(t,f\right)+2Re\left[{\text{WVD}}_{x_1{x}_2}\left(t,f\right)\right]+{\text{WVD}}_{x_2}\left(t,f\right)$ (5)

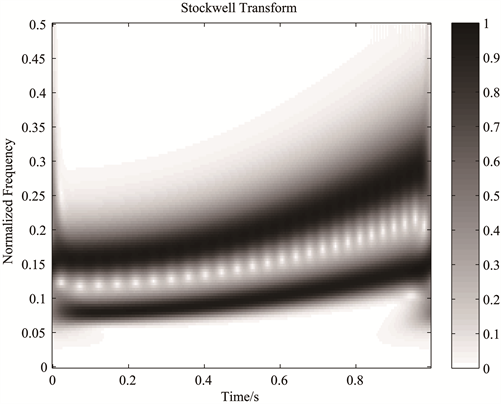
Figure 3. The ST spectrum of the synthetic signal

图3. 合成信号的ST频谱

其中 ${\text{WVD}}_{x_1{x}_2}\left(t,f\right)={\displaystyle {\int }_{-\infty }^{+\infty }{x}_1\left(t+\frac{\tau }{2}\right)x_2^{\ast }\left(t-\frac{\tau }{2}\right)\exp \left(-j2\text{π}f\tau \right)\text{d}\tau }$ 。WVD受交叉项的影响， $n$ 个分量就会产生 $C_n^2=\frac{n\left(n-1\right)}{2}$ 交叉项。这些交叉项在时频面上的振荡，使得频谱图中出现假频、模糊的现象 [25] [26] [27] 。

为了获得更高的时频分辨率，抑制WVD中的交叉项干扰，人们又先后提出了由WVD衍生的核函数光滑法：Cohen类分布 [28] ，仿射类分布 [29] ，自适应最优核方法以及能量再分配方法等 [30] [31] 。前三种方法都是利用相关核函数，如Bessel函数、Born-Jordan函数、a-Wigner-Ville函数、Bertrand函数等对交叉项平滑处理。Cohen类、仿射类分布等核函数方法改善了WVD的交叉项干扰，提高了谱图中信号分量的聚焦性。但是Cohen类与仿射类核函数是固定不变，由于一种核函数只能对一种类型的信号起有效作用，因此自适应核函数法是固定核函数方法的有效改进 [32] 。

图4为本文合成信号的WVD，从图中可以看出，在自项之间存在着交叉项的干扰：

4. 自适应性非参数时频分析方法

4.1. EMD类时频分析方法

除了一些众所周知的英文缩写，如IP、CPU、FDA，所有的英文缩写在文中第一次出现时都应该给出其全称。文章标题中尽量避免使用生僻的英文缩写。Huang等提出的EMD方法能捕捉信号的非平稳特征，是分析非平稳信号的重要方法之一 [14] [33] [34] [35] [36] 。EMD将非平稳信号分解成本征模函数(Intrinsic Mode Functions, IMF)之和的形式，即

$s\left(t\right)=\underset{k=1}{\overset{K}{{\displaystyle \sum }}}{s}_k\left(t\right)$ (6)

其中， $s_k\left(t\right)=A_k\left(t\right)\cos \left({\varphi }_k\left(t\right)\right)$ 为本征模函数。本征模函数的求解是一个“筛选”过程，该过程满足一定筛选次数或残差满足一定范围时结束。通过对各本征模分量的谱分析得到非平稳信号的频谱。由于EMD

Figure 4. The Wigner-Ville distribution of the synthetic signal

图4. 合成信号的WVD频谱

方法能够都对信号实现完全分解，且各分量间是完全正交的，因此频谱不会丢失原信号的信息，能量遗漏也较少。尽管EMD方法简单直观，应用广泛，但是该方法有模态混叠、假频等现象。为了克服以上不足，人们提出了EEMD、CEEMD等方法。

Torres等提出的EEMD [19] 是一种噪声辅助数据分析方法。它对加入不同比例高斯白噪声的信号，即 $s_i\left(t\right)=s\left(t\right)+n_i\left(t\right)$ 进行分解，其中 $n_i\left(t\right),i=1,\cdots ,I$ 是不同标准差的高斯白噪声。对每个 $s_i\left(t\right)$ 进行分解得到相应的IMFs，即

$s_i\left(t\right)=\underset{k=1}{\overset{K}{{\displaystyle \sum }}}{s}_k^i\left(t\right)$ (7)

对全部加噪信号相应的 $s_k^i\left(t\right)$ 分别相加求均值，最终得到总体的平均本征模分量 $\overline{s_k\left(t\right)}=\frac{1}{I}{\displaystyle {\sum }_{i=1}^I{s}_k^i\left(t\right)}$ 。

通过加噪平均的方式，EEMD能得到很好的时频分解结果，纠正EMD中模态混叠、假频等现象。但由于对多组加噪信号的分解处理计算量较大，而且也不能像EMD得到完备的分解。

为取得更有效的时频分解，同时满足信号重构的要求，Torres等人对EEMD进一步完善，并提出了CEEMD [19] 。CEEMD方法分解的第一个IMF求法与EEMD一样，从第二个IMF开始，其求解公式如下：

${\text{IMF}}_{\left(k+1\right)}=\frac{1}{N}\underset{n=1}{\overset{N}{{\displaystyle \sum }}}{E}_1\left[r_k+\xi E_k\left(W_n\right)\right]$ (8)

其中，N表示总的实现次数， $E_k$ 表示EMD过程得到的第k个IMF， $r_k$ 为第k步的分解残差 $r_k=s\left(t\right)-{\displaystyle {\sum }_{i=1}^k{\text{IMF}}_i}$ ， $\xi$ 是高斯白噪声 $W_n$ 的固定参数。CEEMD作为EEMD的扩展，它保留了EMD的完备分解性，在减少计算量的基础上，时频分解效果也比EMD、EEMD好。

图5和图6分别为合成信号的EMD、EEMD频谱图：

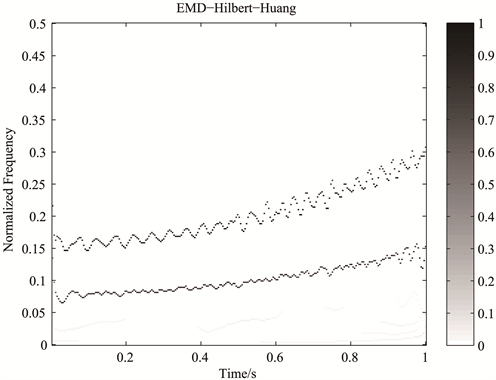
Figure 5. The EMD time-frequency distribution of the synthetic signal

图5. 合成信号的EMD频谱

Figure 6. The EEMD time-frequency distribution of the synthetic signal

图6. 合成信号的EEMD频谱

4.2. Synchrosqueezing类时频分析方法

Daubechies等人提出的SSWT [15] 是一种自适应性方法，该方法将信号分解为独立谐波分量之和形式： $s\left(t\right)={\displaystyle {\sum }_{k=1}^K{A}_k\left(t\right)\times \cos \left({\theta }_k\left(t\right)\right)}+\eta \left(t\right)$ ，其中 $A_k\left(t\right),{\theta }_k\left(t\right)$ 分别为瞬时振幅、瞬时相位， $\eta \left(t\right)$ 为噪声 [37] 。SSWT在CWT的基础上对频谱能量进行再分配，将其集中到瞬时频率上。这种方法可有效抑制拖尾性且可进行信号重构 [38] [39] 。它将CWT的时间尺度域 $\left(a,\tau \right)$ 映射到时间频率域 $\left({\omega }_s\left(a,\tau \right),\tau \right)$ ，其瞬时频率为：

${\omega }_s\left(a,\tau \right)=\frac{-i}{2\text{π}{W}_s\left(a,\tau \right)}\frac{\partial W_s\left(a,\tau \right)}{\partial \tau }$ 。离散SSWT表达式为：

$T_s\left({\omega }_l,\tau \right)=\frac{1}{\Delta \omega }\underset{a_k}{{\displaystyle \sum }}{W}_s\left(a_k,\tau \right)a^{-3/2}\Delta a_k$ (9)

其中， $\text{Δ}{a}_k=a_{k-1}-a_k,\text{Δ}\omega ={\omega }_l-{\omega }_{l-1}$ ，并且 $a_k$ 满足 $\left|\omega \left(a_k,\tau \right)-{\omega }_l\right|\le \Delta \omega /2$ 。SSWT沿着频率(尺度)轴对小波谱进行压缩，使得频谱能量分布更集中。

Zhonglai Huang等人提出的压缩S变换 [40] (SSST)对S变换进行压缩，使能量聚集在瞬时频率。瞬时频率为：

$\tilde{f}\left(f,b\right)=f+{\left[i2\text{π}S{T}_x\left(f,b\right)\right]}^{-1}\times \frac{\partial S{T}_x\left(f,b\right)}{\partial b}$ (10)

其中， $S{T}_x\left(f,b\right)=\frac{\left|f\right|}{\sqrt{2\text{π}}}{\displaystyle {\int }_{-\infty }^{+\infty }x\left(t\right){\text{e}}^{\frac{-{\left(t-b\right)}^2{f}^2}{2}}{\text{e}}^{-i2\text{π}ft}\text{d}t}$ 。由上式得到SSST公式如下：

${\text{SSST}}_x\left({\tilde{f}}_l,b\right)={\left(\Delta \tilde{f}\right)}^{-1}\times \underset{f_k:\left|\tilde{f}\left(f_k,b\right)-{\tilde{f}}_l\right|\le \frac{\Delta \tilde{f}}{2}}{{\displaystyle \sum }}\left|S{T}_x\left(f_k,b\right)\right|f_k\Delta f_k$ (11)

这里 $f_k$ 是计算ST时的离散频率值， $\Delta f_k=f_k-f_{k-1},\Delta \tilde{f}={\tilde{f}}_l-{\tilde{f}}_{l-1}$ 。SSST与SSWT相比，两种方法都能对信号进行重构且有较小误差。图7为合成信号的SSWT的频谱图，从图中可以看出，信号的能量集中在瞬时频率的“脊”线上，具有较高的时频精度。

5. 自适应性参数时频分析方法

自适应性参数时频分析方法是基于原子字典库 $D={\left\{{\Psi }_r\right\}}_{r\in D}$ 寻找信号的稀疏表示 [41] - [46] 。这种方法能消除交叉项干扰，提高时频分辨率。

Figure 7. The SSWT time-frequency distribution of the synthetic signal

图7. 合成信号的SSWT频谱

5.1. 匹配追踪算法(MP)

匹配追踪算法(MP)基于字典 $D={\left\{{\Psi }_r\right\}}_{\Psi \in D}$ 对信号 $s\left(t\right)$ 进行分解 [21] ，其原子形式为：

${\Psi }_r\left(t\right)=\frac{1}{\sqrt{a}}\Psi \left(\frac{t-\tau }{a}\right){\text{e}}^{i\omega \left(t-\tau \right)}$ ，这里 $r=\left(a,\omega ,\tau \right)$ ，信号分解为如下形式：

$s\left(t\right)=\underset{n=0}{\overset{N-1}{{\displaystyle \sum }}}{a}_n{\Psi }_{r_n}\left(t\right)+R^{\left(n\right)}s$ (12)

其中， $N$ 为总迭代次数， $a_n$ 为小波 ${\Psi }_{r_n}\left(t\right)$ 的振幅， $R^{\left(n\right)}s$ 为第n次迭代的残差， $R^{0}s=s$ 。由于寻找最优

信号分解的问题是一个NP问题，MP利用贪婪算法从字典中寻找信号的次优分解，步骤如下：

1) 将信号 $s\left(t\right)$ 近似投影到向量 ${\Psi }_{r_0}\left(t\right)\in D$ 上： $s=\langle s,{\Psi }_{r_0}\rangle {\Psi }_{r_0}+R^{1}s$ ，这里残差 $R^{1}s$ 与原子 ${\Psi }_{r_0}$ 是正交的，且 ${\Psi }_{r_0}$ 满足 $\left|\langle s,{\Psi }_{r_0}\rangle \right|=\underset{r\in D}{\sup }\left|\langle s,{\Psi }_r\rangle \right|$ ， ${\Vert s\Vert }^2=\left|\langle s,{\Psi }_{r_0}\rangle \right|+{\Vert R^{1}s\Vert }^2$ ，使得 $\Vert R^{1}s\Vert$ 达到最小。

2) 进入步骤(1)，迭代至第 $k$ 步，在字典中筛选出与残差 $R^{k}s$ 有最大相关性的原子 ${\Psi }_{r_k}:\left|\langle R^{k}s,{\Psi }_{r_k}\rangle \right|=\underset{r\in D}{\sup }\left|\langle R^{k}s,{\Psi }_r\rangle \right|$ ，残差 $R^{k+1}s:=R^{k}s-\langle R^{k}s,{\Psi }_{r_k}\rangle {\Psi }_{r_k}$ ，即： ${\Vert R^{k+1}s\Vert }^2={\Vert R^{k}s\Vert }^2-\left|\langle R^{k}s,{\text{Ψ}}_{r_k}\rangle \right|$ 。

3) 当迭代至第n步， $s={\displaystyle {\sum }_{k=0}^{n-1}\langle R^{k}s,{\Psi }_{r_k}\rangle {\Psi }_{r_k}}+R^{n}s$ ，且 ${\lim }_{n\to \infty }\Vert R^{n}s\Vert =0$ 时迭代结束，因此可得到： $s={\displaystyle {\sum }_{n=0}^{+\infty }\langle R^{n}s,{\Psi }_{r_n}\rangle {\Psi }_{r_n}}$ ，能量函数为： ${\Vert s\Vert }^2={\displaystyle {\sum }_{n=0}^{+\infty }{\left|\langle R^{n}s,{\Psi }_{r_n}\rangle \right|}^2}$ 。

MP提供的灵活算法自适应地从时频字典中选择出符合信号结构的字典原子，再从这些原子的尺度、频率、时间相位中，得到信号分量的一些明确特性。因此，MP可以很好的应用在信号处理中。

图8为合成信号的MP的时频图：

Figure 8. The MP time-frequency distribution of the synthetic signal

图8. 合成信号的MP频谱

5.2. 基追踪算法(BP)

另一种自适应性参数时频分析方法是基追宗(BP)，它的主要原理与MP类似。信号表示为字典中原子的稀疏表示，即 $s\left(t\right)={\displaystyle {\sum }_{n=1}^N\Psi \left(t,n\right)\ast a\left(t,n\right)}$ ，这里 $N$ 表示原子数， $\Psi \left(t,n\right)$ 为小波原子， $a\left(t,n\right)$ 为相关系数。信号分解的矩阵表示为：

$s=\left({\Psi }_1,{\Psi }_2,\cdots ,{\Psi }_N\right)\left(\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_N\end{array}\right)+\eta =D\alpha +\eta$ (13)

其中， ${\Psi }_n$ 表示 $\Psi \left(t,n\right)$ 的卷积矩阵， $D$ 为小波字典， $\eta$ 为噪音。BP从初始模型开始，从字典中选择出合适的原子，来替换原模型中的分量。通过解决以下两个问题得到了更好的稀疏表示：1) 最小化 ${\Vert \alpha \Vert }_1$ 即 $\alpha$

的 $l_1$ 范数，使得 $D\alpha =s$ ；2) 最小化 $J=\frac{1}{2}{\Vert s-D\alpha \Vert }_2^2+\lambda {\Vert \alpha \Vert }_1$ ，这里函数J的第一项是基于 $l_2$ 范数的误差项，

$\lambda$ 为惩罚参数，用来权衡误差项与非零系数之间的关系，以便找到稀疏表示的最优解，这是BP与MP最大的不同，也是BP比MP更广泛应用的原因。

6. 结论

本文对时频分析方法进行了综述性介绍。主要方法有：线性时频分析、二次时频分析、自适应性非参数时频分析和自适应性参数时频分析。近些年时频分析方法主要有压缩类时频分析，如压缩小波变换，压缩S变换等等。时频分析方法多种多样，不能够武断的说一种方法具有绝对的优势。针对不同类型的信号，需要选择合适的方法来进行分析。