1. 引言
球磨机作为一种重要的物料研磨加工设备,广泛应用于冶金、化工等行业。磨机内部负荷参数是研磨过程的重要工艺指标。球磨机负荷的精准检测对于提高研磨过程效率、改善研磨产品质量至关重要 [1] 。
目前研磨过程中湿式球磨机负荷检测多依赖现场专家经验,或在筒体内安装传感器直接检测,直接检测方法存在传感器易损坏、维修不方便的局限。利用球磨机易测的外部响应信号,预报球磨机负荷内部参数的间接测量方法,由于实施简单,日益受到重视 [2] [3] 。目前广泛采用的磨机负荷间接检测方法多基于振动、振声或电流信号判断球磨机负荷参数或者运行状态 [4] 。文 [5] 采用核主元分析提取振动信号频谱特征,在非线性频谱特征空间内选用学习速度快、泛化性好的ELM建立集成模型个体,有效克服单一ELM个体模型存在的运行结果不稳定问题。
尽管球磨机筒体表面振动加速度信号、振动声响信号和电流信号数据丰富,但信息贫乏,基于数据的建模是一个挑战性的任务。影响磨机负荷测量模型性能的振动、振声频谱变量维数高达成千上万维,尤其是随着数据规模增大,球磨机负荷模型对计算机性能的要求越来越高,计算任务庞大到单台计算机无法完成或是任务完成所需的时间很长,传统集中式机器学习处理大规模数据时,存在通信开销大、算法时间和空间复杂度高等问题。在工业数据规模庞大的背景下,如何利用现有的计算资源实现大规模数据的分布式学习问题有待解决。文 [6] 提出一种训练数据分布在分散信息结构下的随机向量功能链接RVFL网络分布式学习算法,算法学习过程中不需要中心代理协调,目标是建立一个通用的学习模型,用于优化局部全体数据的系统性能。
本文针对传统集中式机器学习算法处理大规模数据计算复杂度高问题,基于交替方向乘子法(ADMM),提出一种球磨机负荷分布式随机权值神经网络建模方法,局部节点采用正则化随机权值功能连接RVFL网络,全局球磨机负荷模型参数采用分布式优化学习ADMM方法交替迭代更新求解。实验结果表明,基于ADMM-RVFL的球磨机负荷模型在计算速度和精度方面具有相对优越性。
2. 预备知识
2.1. 交替方向乘子法ADMM计算框架
交替方向乘子法 [7] (Alternating direction method of multipliers, ADMM)是一种求解有约束最优化问题的计算框架,适用于求解大规模分布式计算系统具有可分离变量的凸优化问题 [8] 。ADMM通过分解协调机制,将大的全局问题分解为多个较小、较容易求解的局部子问题,并通过协调子问题的解而得到大的全局问题的解。
ADMM一般用于求解可分离目标函数的凸优化问题:
(1)
其中
为优化变量。矩阵
。函数
和函数
分别是关于
的凸函数。构造增广拉格朗日罚函数为:
(2)
其中
是对偶变量,常量
。
ADMM算法迭代步骤如下:
(3)
(4)
(5)
ADMM算法类似于增广拉格朗日乘子法,实际上,也可以通过采用增广拉格朗日乘子法进行迭代求解
。如果已知道
时刻
数值大小,则求得:
(6)
(7)
比较方程(3) (4) (5)和(6) (7),前者采用ADMM算法,交替更新
变量,后者采用增广拉格朗日乘子法,同时更新
变量。它们的共同之处是先通过迭代的方法求解变量
,然后再求解出对偶变量
。ADMM的命名也因此而来,这种算法和Gauss-Seidel方法有点类似。相对于增广拉格朗日乘子法,ADMM算法交替迭代更新方式更容易计算求解。因此,ADMM算法在分布式求最优解问题得到广泛应用。
2.2. RVFL神经网络模型
随机向量泛函连接网络(Random Vector Functional Link,简称RVFL)是一种随机权值神经网络 [9] 。假设输出
,RVFL神经网络可以描述为L个隐含层节点输出的加权和:
(8)
第
个变换通过向量
进行参数化,输入是一个d维的实向量
。每一个
称为一个基,隐函数,函数链接。在仿真中使用sigmoid基础函数:
(9)
在学习过程的开始就要选择
,而与训练数据无关。在RVFL神经网络中,隐函数的参数从一个预先定义的概率分布中随机选择。假设基函数是连续的和平稳的,且提供足够多的隐层函数,当L足够大的条件下,RVFLs普遍逼近能力才能够得到保证。通过使用这种方法,方程(8)可以转化为关于系数
的线性回归方程。假如提供N个样本的所需函数,称为一个训练。即
。
记
(10)
通过使用一个标准的正则最小二乘法可以求得最优参数
(11)
令
的梯度为零,即:
(12)
可以计算得到:
(13)
其中
是一个单位矩阵,
矩阵求逆影响RVFL的计算复杂度,但是在
的情况下,可以通过下面方程进行简化,对于任意
,有:
(14)
结合方程(13)和(14),可以得到求得最优权重
的另一个方程:
(15)
3. 基于ADMM-RVFL的神经网络分布式学习算法
基于RVFL的分布式学习模型,这种方法的训练数据在分散信息结构下是均匀分布的。在此模型下采用了交替方向乘子(ADMM)算法。这个算法以一个完全分布式的方式工作,在学习过程中并不需要中央代理的协调。分布式学习的目的是建立一个共同的学习模型,在整个本地数据集中优化整个系统性能。在这项工作中,它是假定所有网络节点都知道输入数据层的初始权值,本地的RVFL网络输出权值仅可以通过相邻节点之间通信信道共享。通过基准数据集对学习算法进行评估。实验结果表明,基于ADMM的学习算法计算虽然复杂,但是精度很高。具体算法推导过程在文 [7] 可见,可以求得:
(16)
更新
和
(17)
(18)
其中已知:
(19)
(20)
假如在一个节点上,
,我们可以利用矩阵求逆引理,以获得更方便矩阵求逆的步骤。
(21)
在第k节点的算法收敛通过计算“初始残差”
和对偶残差
,其定义分别为:
(22)
(23)
停止标准是两个残差应该小于两个阈值:
(24)
(25)
选择阈值的方式:
(26)
(27)
其中
和
分别是特定的绝对和相对误差。表1中给出ADMM-RVFL分布式学习方法伪代码。
4. 实验仿真结果与分析
4.1. 实验对象描述
实验数据来源于XMQL 420 × 450格子型球磨机数据采集系统,如图1所示。其中振动加速度传感器安装在球磨机中部筒体外表面上,采样频率为51,200 Hz,声音传感器安装在距球磨机入口1/3处,采样频率8000 Hz。球磨机最大钢球装载量为80 Kg,磨粉能力为10 Kg/小时,转速为57转/分钟。研磨实验方案是在球磨机筒体内添加不同配比(直径30、20和15 mm)的钢球、铜矿石和水,混合均匀后研磨运

Table 1. Distributed ADMM-RVFL algorithm
表1. 分布式ADMM-RVFL算法
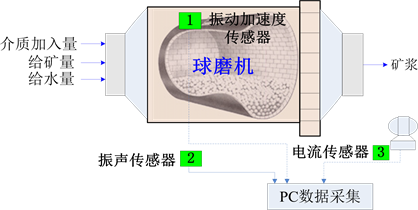
Figure 1. Signal acquisition of experimental ball mill
图1. 实验球磨机信号采集
行1分钟后清洗球磨机。
球磨机负荷模型输入包括振动加速度信号频谱,振声信号频谱,电流信号,输出是料球比、磨矿浓度、填充率三个球磨机负荷参数。其中振动信号频谱维数高达12,500维,振声信号频谱维数4000维。
4.2. MATLAB分布式计算集群配置
实验环境MATLAB分布式计算集群需要分布式计算工具箱和计算引擎MDCE。分布式计算集群配置方法需要开启MDCE,设置客户端(Client)、调度或作业管理器(Scheduler/Jobmanager)和计算节点(Worker)。本文选择一台PC机(Win7系统)作为服务端,一台PC机(Win7系统)和一台笔记本电脑作为客户端(Win7系统),服务器和客户端均安装了一致的MATLAB(2012a)版本。首先将服务器和客户端配置在同一个局域网内并且Ping通,保证服务器和客户端可以相互通信。然后安装mdcs (MATLAB Distributed Computing Server)等服务,配置集群,把计算资源连接在一起,最后调用集群,训练分布式学习模型,并测试分布式模型性能。
4.3. 球磨机实验结果和分析
本实验采用Lynx工具箱。经过测试分析,磨机负荷模型优化的参数
为2−2,
为1.5,
为0.25,
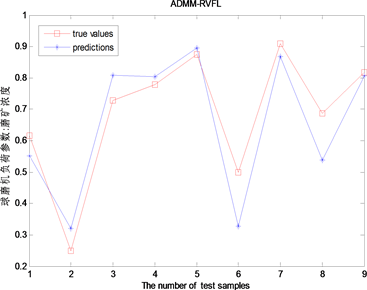
为0.01,C为1,隐含层节点数为200,迭代次数为100,work数为6。采用均方根误差(root mean square error, RMSE)、均方误差(mean square error, MSE)、均绝对值误差(mean absolute error, MAE)对模型性能进行评价。图2(a)~图2(c)为分布式ADMM-RVFL球磨机负荷预报结果,X轴表示测试样本个数,Y轴表示料球比、矿浆质量分数、负荷充填率。表2中分别采用均方根误差(root mean square error, RMSE)、均方误差(mean square error, MSE)、均绝对值误差(mean absolute error, MAE)作为模型性能评价指标,其定义分别如下:
(28)
(29)
(30)
采用测试数据集对所提模型进行验证,为了进一步检验本文所提方法的有效性,分布式ADMM-RVFL与集中式RVFL(Centralized-RVFL)、一致性RVFL(CONS-RVFL)模型进行对比分析。本文以填充率为例,分布式ADMM-RVFL球磨机负荷参数填充率预报结果对比如图2和表2所示。对于集中
 (a)
(a) 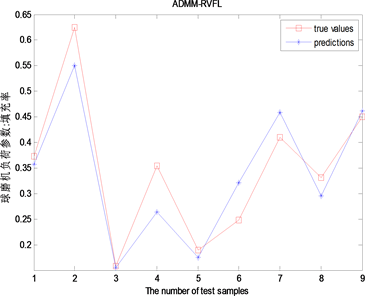 (b)
(b)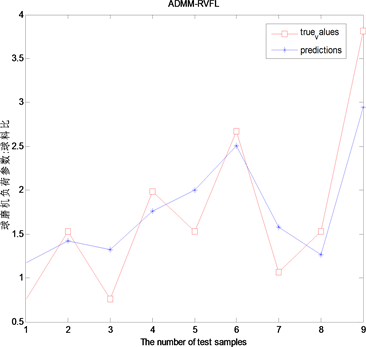 (c)
(c)
Figure 2. Forecast results of mill load with ADMM-RVFL
图2. ADMM-RVFL对球磨机负荷的预报结果

Table 2. Mill load parameter results with ADMM-RVFL models
表2. 球磨机负荷参数ADMM-RVFL建模结果
式RVFL,收集所有可用的训练数据集中存储在一个节点,训练一个RVFL神经网络模型。对于一致性RVFL,数据均匀地分布在整个网络中。基于ADMM-RVFL设置了一个上限400次的迭代,迭代误差阈值
,
。通过以上实验对比及表3可知,集中式C-RVFL以及ADMM-RVFL神经网络模型填充率预报效果较好,误差率较低,具有更高的精度和模型泛化性。

Table 3. Comparison of forecasting results of filling rate with different modeling methods
表3. 不同建模方法填充率预报结果比较
5. 结论
本文基于分布式ADMM-RVFL算法,建立了球磨机负荷参数料球比、磨矿浓度和填充率分布式神经网络模型。仿真实验结果表明分布式ADMM-RVFFL算法与集中式、一致性神经网络模型相比,模型计算与存储的开销大大减少,具有相对较高的精度,克服了传统磨机负荷检测方法存在的测量精度低、性能不稳定等缺陷。
基金项目
国家自然科学基金资助(项目号:61203102)。