累积剩余熵的若干基本性质及其在股票分析中的应用

The Basic Properties of Accumulated Residual Entropy and Its Application in Stock Analysis

摘要: 在信息熵的基础上，我们进一步研究累积剩余熵的一些性质，并将累积剩余熵模型应用于风险度量中。再在实际应用中，选取8支股票，收集每日收盘价格数据，利用SPSS软件绘制累积剩余熵与标准差的关系图，得出累积剩余熵与标准差的线性关系，又因为累积剩余熵的适用范围比方差更广，即在度量风险中，累积剩余熵模型比方差更具有优势。

Abstract: On the basis of information entropy, we further study some properties of the cumulative residual entropy, and the cumulative residual entropy model applied in risk measure. In practical applica-tions, the selection of eight stocks, collect the daily closing price data, using SPSS software to draw the cumulative residual entropy and the standard deviation of the diagram. It is concluded that the cumulative residual entropy and the standard deviation of the linear relationship, and because of the cumulative residual entropy of a broader scope than variance, namely in the risk measurement, the cumulative residual entropy model has more advantages than the variance.

1. 引言

金融市场随着时间的演化，越来越多的因素影响着它的变化，随着金融市场的复杂化，越来越多的人试图运用各种方法探索它的变化规律，以求获得利益。投资者获得的收益可能与期望不一致，因为投资具有很大的风险，通常巨大的利益常伴随着巨大的风险，金融市场中存在的各种各样的风险，这种风险越来越引起人们的重视，只有正确理解什么是金融风险，掌握影响金融风险的因素有哪些，才能恰当的度量金融风险，为金融活动提供有力保障。

风险一般有两种理解：一种强调了风险表现为收益不确定性；另一种则强调风险表现为成本或代价的不确定性。金融风险是指金融资产在未来时期内预期收入遭受损失的可能性，即金融风险与损失的不确定性有关。无论是对损失还是收益，风险都表现出一种不确定性，这种不确定性体现出风险的本质。为了减少损失，扩大收益，人们试图采用各种方法去度量风险，即利用已知数据来分析未来不确定事件的不确定性以及可能带来的损失或收益。

现有的度量风险方法有很多种，例如：波动性方法即方差(均方差)方法 [1] 、 $Var$ 方法 [2] 、灵敏度方法 [3] 、一致性风险度量方法 [4] 和失真函数方法 [5] 等等。每种方法都有它的优点和它的局限性。

20世纪，shannon提出了一个对离散随机变量不确定性的度量，即shannon熵，这与风险的本质相吻合。近年来，越来越引起人们的关注与研究，并将熵应用于金融投资组合、风险度量和数据压缩等领域中。本文中如无特别说明，总假定log是以2为底的对数。对于离散随机变量 $X$ ，其shannon熵 [6] 的定

义为： $H\left(X\right)=-{\displaystyle \underset{x}{\sum }p\left(x\right)}\log p\left(x\right)$ ，其中 $p\left(x\right)$ 是随机变量 $X$ 的概率密度函数， $0\le p\left(x\right)\le 1$ ， ${\displaystyle \underset{x}{\sum }p\left(x\right)}=1$ ，并约定 $0\ln 0=0$ 。当随机变量 $X$ 是连续型时，我们称其不确定性的度量为微分熵，其定义为： $h\left(X\right)=-{\displaystyle \underset{s}{\int }f\left(x\right)}\log f\left(x\right)\text{d}x$ ，其中 $f\left(x\right)$ 是随机变量 $X$ 的概率密度函数， $s$ 是 $X$ 的支撑集(即使 $f\left(x\right)>0$ 的所有 $x$ 构成的集合)。

但shannon熵也存在一些不足，例如：假设 $X$ 和 $Y$ 是两个离散的随机变量， $X$ 的取值空间是

$\left\{1,2,3,4,5,6,7,8\right\}$ ，每一个的取值概率都为 $\frac{1}{8}$ ， $Y$ 的取值空间是 $\left\{1,2,3,4,5,6,7,10000\right\}$ ，每一个的取值概率也都为 $\frac{1}{8}$ ，则 $H\left(X\right)=-{\displaystyle \underset{i=1}{\overset{8}{\sum }}\frac{1}{8}}\log \frac{1}{8}=\frac{27}{8}=H\left(Y\right)$ ，即 $X$ 和 $Y$ 的shannon熵是一样的，但如果 $X$ 和 $Y$ 代表的

是博弈游戏中两个不同的回报方案，显然随机变量 $X$ 和 $Y$ 包含的信息量是不同的，但shannon熵对此并加以区分。为了克服shannon熵的一些不足，Murali Rao等提出了一种新的熵概念，即累积剩余熵(Cumulative Residual Entropy，简记为CRE)。

2. 累积剩余熵的基本性质

定义： [7] 设 $X\in R^N$ 是一个随机向量，则 $X$ 的CRE定义为：

$\epsilon \left(X\right)=-{\displaystyle {\int }_{R_{+}^N}P\left(\left|X\right|>\lambda \right)}\log P\left(\left|X\right|>\lambda \right)\text{d}\lambda$

其中 $X=\left(X_1,X_2,\cdots ,X_N\right)$ ， $\lambda =\left({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_N\right)$ ，并且 $\left|X\right|>\lambda$ 意味着

$\left|X_i\right|>{\lambda }_i,i=1,\cdots ,N,R_{+}^N=\left\{x_i\in R^N;x_i\ge 0\right\}$ .

性质1： 若存在 $p>N$ ，使得对任意的 $i$ ， $E\left({\left|X_i\right|}^p\right)<+\infty$ 恒成立，则 $\epsilon \left(X\right)<+\infty$ 。

性质2： [7] 对于任意的非负且独立的随机变量 $X$ 和 $Y$ ，有 $\max \left(\epsilon \left(X\right),\epsilon \left(Y\right)\right)\le \epsilon \left(X+Y\right)$ 。

性质3：(条件使熵减少) 对任意的 $X,Y\in R^N$ ，有 $E_X\left[\epsilon \left(Y|X\right)\right]\le \epsilon \left(X+Y\right)$ ，当且仅当 $X,Y$ 相互独立时，

等号成立。

此性质说明当已知条件越多时，未来事件的不确定性就下降了，即风险降低了。

此外，累积剩余熵中，由于 $p\left(x>\lambda \right)=1-F\left(\lambda \right)$ ，其中 $F\left(\lambda \right)$ 是其经验分布函数，在实际应用中，经验分布函数更容易得到，若对已知的分布，只需按定义即可计算出其剩余熵，若随机变量的分布形式未知，则可依据下面的定理，用经验 $\mathrm{CRE}\left(\epsilon \left(F_n\right)\right)$ 逼近 $\mathrm{CRE}\left(\epsilon \left(F\right)\right)$ 。

设 $X_1,X_2,\cdots ,X_n$ 是正的且是独立同分布的随机变量， $F$ 是其分布函数，令 $F_n$ 是 $n$ 个样本的经验分布，且每个样本的概率都是，令，则经验分布的CRE为。

性质4： [7] 设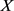，是空间中任意的随机变量，则它的经验CRE收敛于CRE，即

性质5：设是随机变量，若的方差存在，则的累积剩余熵存在。

证明：由于的方差存在，即，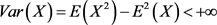

所以

,

由性质1可得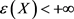，，即的累积剩余熵存在。

由性质5，我们可以看出，只要随机变量的方差存在，则其累积剩余熵必存在，反之，当累积剩余熵存在时，方差是否存在呢？为此我们以Pareto分布为例比较一下。

Pareto分布是一种比较常见的厚尾分布，厚尾分布是金融市场中比较常见的分布。首先，我们了解一下Pareto分布的密度函数，

由此可得，其方差为：

其累积剩余熵为：

由以上方差与累积剩余熵的算式，我们可以看出，当时，其累积剩余熵存在，但其方差不存在，即累积剩余熵的适用范围比方差更广。

下面我们研究一下，当随机变量的方差与累积剩余熵都存在时，方差与累积剩余熵是否有关系。首先，我们比较一下几种常见分布的方差与累积剩余熵。

1) 均匀分布的CRE。

设，则

,

即

2) 指数分布的CRE。

设，则

,

则

3) Pareto分布的CRE。

由上面的分析，当时，

由以上几个例子，可以看出随机变量的累积剩余熵与它的标准差呈线性关系。

3. 实证分析

下面我们举例看一下它的应用。

例现有两个转盘A,B的抽奖游戏，中奖的钱 (单位：元)以及概率如表1，表2所示：

Table 1. The amount and probability of A winning the turntable A

表1. 转盘A中奖的钱数及概率

Table 2. The amount of money and probability of winning the turntable B

表2. 转盘B中奖的钱数及概率

由表1，表2，我们可以计算出它们的均值、方差、熵以及累积剩余熵，比较一下，哪一个更准确。

首先计算出均值：，即从均值的角度看，两个转盘游戏是一样的，风险相同。

其次计算出方差：，即从方差的角度看，转盘2的波动比较大，风险更高。

下面计算熵：

因为，即转盘1的风险更高，但此与实际不符。

最后我们看一下它们的累积剩余熵：

首先，设为它们的分布，，，

,

则

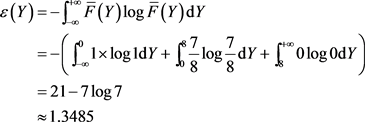
显然，，即转盘2的风险大于转盘1的风险。

对于独立同分布的随机变量，是其分布函数，随机变量的经验分布函数为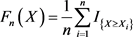，，其中是示性函数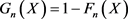，，首先，可以先将个样本按从小到大的顺序重新排列，使得。则

为了分析股票市场中的不确定性，下面选了8支股票(海螺水泥，长城汽车，工商银行中国国航，青岛啤酒股份，马鞍山钢铁股份，大唐发电以及中国石油股份)的每日收盘价格(从2014年1月3日到2017年8月30日)为样本(数据来源：东方财富网)。

根据相应的公式，我们可以计算出8支股票对应的平均值、标准差、偏度(偏态的系数)、峰度(峰态的系数)以及累积剩余熵(CRE)，如表3所示。

由表3可以看出，8支股票都有一定的偏度和峰度，不是标准的正态分布，而且由上表，我们可以看出标准差与累积剩余熵有一定的联系，标准差大的股票，其对应的累积剩余熵也较大；标准差小的股票，其对应的累积剩余熵也较小。

为了进一步观察标准差与累积剩余熵的关系，我们在8支股票中任选一支股票，例如中国石油股份，将其900个数据(从2014年1月3日到2017年8月30日)按时间顺序分成15份，如表4所示。

Table 3. The values of each of the eight stocks

表3. 8支股票对应的各参数值

Table 4. Standard deviation and CRE of petrochina

表4. 中国石油股份的标准差与CRE

由表4我们可以画出标准差与累积剩余熵的图形，如图1~3所示。

由图3，我们可以看出标准差与累积剩余熵呈线性关系。由以上分析，我们可以看出，当方差波动较大时，累积剩余熵 [5] 也变大，反之，则累积剩余熵变小。当经验分布是重尾的时，累积剩余熵比方差更有利。特别是当经验分布服从Levy分布时，其均值与方差不存在，无法利用方差度量时，累积剩余熵仍然可以计算出来。累积剩余熵的计算比较简单，容易实现，由于经验分布趋向于总体分布，而经验分布是比较容易得到的，而且不论是连续型随机变量还是离散型随机变量，都可以利用累积剩余熵计算出来。虽然金融市场的复杂性很大，针对不同的风险源有不同的度量方法，但累积剩余熵在金融投资中有一定的实际意义。

Figure 1. Sequence diagram of CRE

图1. CRE序列图

Figure 2. The standard deviation sequence diagram

图2. 标准差的序列图

Figure 3. The linear correlation between standard deviation and CRE

图3. 标准差与CRE之间的线性相关性

致谢

感谢我的导师对我的悉心教导，感谢我的同学和朋友在学习、生活上的关心和帮助，最后，感谢我的家人，一直以来，无论是学习和生活，都离不开他们的支持、照顾和理解。

基金项目

安徽工业大学研究生创新基金资助(2016137)。