1. 引言
动车司机室是一个相对狭小的空间,长时间后容易让驾驶员产生生理和心理上的不适应感 [1] ,由室内微气候影响的热舒适性是其重要部分。室内微气候是指室内环境的气候条件,包括气温、湿度、空气流速以及室内材料的热辐射,其气候舒适性不仅是司机关注的问题,也是动车设计初期需要考虑的重要内容。室内微气候主要由采暖、通风和空调(Heating、Ventilating and Air Conditioning, HVAC)系统来控制,在设计早期就需要预测HVAC系统对司机气候舒适性的影响( [2] , p. 116)。
UIC 651:2002标准对动车HVAC系统的设计做出了下列规定:1) 对于采暖,要求司机头部附近温度处于18℃~23℃范围内;在司机室内较高处和较低处区域的温度差不应超过10℃;当外部温度很低时,允许降低温度范围但采暖发热能力应保证至少18℃的温度。2) 通风时要求司机头顶上的空气流速不超过0.3 m/s;应保证每人每小时至少30 m3的气流量,每个司机室每小时至少300 m3的空气量。
人体热舒适感觉非常复杂,它与人体所处环境以及人体自身因素有关。多年来建立了不少人体热舒适性模型,如Fanger稳态模型和Gagge等人的二节点瞬态模型,但两种模型只给出了创造热环境的变量组合,没有考虑人体所处的非均匀热环境对人体热舒适性的影响( [2] , p. 104)。对于轿车室内的非均匀热环境下的人体热舒适性,孙一宁提出了修正的加权PMV算法和基于当量温度指标的整体热感觉舒适性偏差AEQT [3] 。靳艳梅利用当量温度指标Teq评价了不同环境下人体的热舒适性,证明了当量温度指标可以很好地评价非均匀热环境下的人体热舒适性 [4] 。对于轨道车辆的室内热舒适性,陈祥利用问卷调查的方式得到高速铁路客车的乘坐舒适度综合评价模型 [5] ,但是问卷的研究方式主观性太大,缺乏实验指导。国际上也有学者利用数值分析研究车辆乘坐空间的热环境 [6] [7] [8] [9] ,但上述研究很多都是针对汽车乘员舱或者轨道车辆的乘客舱进行分析,并且只是计算出了物理量,并未按照切实的评价标准对舒适性进行合理的评价。由于微气候下,人体热舒适性受人和外部环境共同作用的影响,因此有必要同时考虑环境和人体因素来研究司机室的热舒适性,从而综合全面地评价人体的热舒适性。
本文建立了动车司机室几何模型,利用CFD数值仿真的方法对冬季和夏季两种工况下司机室内的空气速度场和温度场进行了仿真,结合UIC 651:2002标准评价司机室内的环境因素,并利用当量温度指标对模拟结果进行了分析,综合评价了司机室的热舒适性。
2. 司机室内传热分析
动车司机室见图1。由于受内外环境影响,室内空气流动和热传递较为复杂。影响司机热舒适性的因素主要包括外界环境参数、司机室几何参数和材料热物理特性参数、HVAC系统参数以及座椅安装、乘员散热等。
司机室内的热交换主要有通过流体的热传递、物体的热传导以及辐射形式的热交换,热传递可以用式(1)表示[1]。
(1)
式中,C为人体对流热损失,单位是W/m2;AD为人体杜波依斯面积,单位是m2;fc1为着衣体表面积与裸体表面积之比;hc为对流换热系数,单位是W/(m2×K);tcl为衣服表面的平均温度,ta为空气温度,单位是℃。

Figure 1. Geometric assembly model of driver compartment and wind hatch positions
图1. 司机室几何装配模型及风口位置示意图
考虑司机室内物体(座椅、地板、仪表板、车窗等)会通过热传导的方式与相邻存在温差的物体进行热交换 [10] ,
(2)
式中,mi为该物体质量;Cpi为该物体定压比热容;Tk为流体温度;hi为该物体面和周围流体间的对流换热系数;Ai为物体及流体间接触面积;Aij为两物体接触面积;Ti为物体温度;Tj为另一物体的温度;li、lj为两物体长度;ki、kj为热传导系数;
为辐射项。可以将车厢内的辐射分为太阳辐射和车厢内环境辐射两部分。假设司机室内空气为透明介质,则
表示为 [10]
(3)
式中,Ai为物体及流体间接触面;
、
分别为该物体对太阳及车内环境辐射吸收率;Gso,i、Gen,i分别为物体表面接收到的太阳辐射强度及环境辐射强度;ε为物体辐射发射率;
为斯蒂芬-波尔兹曼常数;Ti为物体温度。
3. 司机室数值模型
3.1. 物理模型
研究对象选为某动车组司机室(图1),司机室的整体几何尺寸为:长3519 mm,宽2618 mm,高2048 mm;室内一个座椅;空调风道结构见图1;共有七个进风口和一个出风口,风口位置见图1,风口参数见表1,回风口位于司机室顶部。
3.2. 数学模型
司机室内空气的流动满足连续性方程和动量方程,在直角坐标系下,两方程如式(4)和式(5) ( [1] , p. 119):
(4)
(5)
式中:ρ 为流体的密度;t为时间;ui、uj 为流体瞬时速度;xi,xj 为位置坐标;P为压力;
为动力粘性系数;Fi为微元体中的体力。
流体在流动中常存在湍流,其物理参数随时间与空间发生随机的变化,是一种高度复杂的三维非稳态的不规则流动,目前尚未有很成熟的湍流理论,出于工程的需要,常采用数值计算方法来近似模拟,

Table 1. Wind hatch parameters of driver compartment
表1. 司机室风口参数
而标准k-e模型是现在很多流体分析软件的湍流理论基础( [1] ,p. 120)。k-e模型可以用式(6)和式(7)表示。
(6)
(7)
式中:μ为动力粘性系数;μt为涡粘性系数;σk为k的涡流普朗特常数;Gk为由于平均速度梯度产生的湍流动能;Gb为由浮力而产生的湍流动能;Ym为可压缩流体中波动膨胀对于全部耗散率所占的比率;Sk、Sε为用户定义的源项;Cε1、Cε3和Cε3为常数。文献 [11] 推荐值为Cε1 = 1.44,Cε2 = 1.92,Cε3 = 1,σk = 1,σε = 1.3。
因为司机室内存在热交换,所以求解司机室内的温度分布还需要补充能量方程( [1] ,p. 119) (式8)。
(8)
式中:Cp为比热容;T为温度;k为流体的传热系数;ST为流体的内热源和由于粘性作用流体机械能转换为热能的部分。
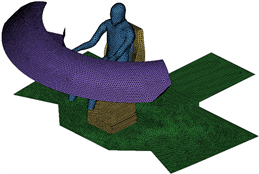
根据求解问题,为突出HVAC系统对司机室内温度场以及空气速度场的影响,对司机室模型做出如下简化:1) 司机室内气流为稳态湍流,流动为各向异性,并且空气不可压缩;2) HVAC系统各风口相互独立,出风温度、速度恒定;3) 忽略仪表台上的按键等部件对室内空气流动的影响,简化仪表台结构,见图2;4) 假设司机室密封良好。根据简化结果,利用非结构网格划分方法建立了司机室的网格模型,对于风口部位的网格进行细化,网格总数为377万得到有限元模型如图2。
3.3. 边界条件设置
边界条件的设置按照企业经验数据选择。
1) 以HVAC系统的进风口作为速度入口边界条件。进风温度夏季为18℃,冬季为28℃。进风速度:顶板进风口为6 m/s,侧窗进风口为3 m/s,腿部进风口为5.5 m/s,前窗进风口为1 m/s。
2) 以HVAC系统的回风口作为出口边界,设为压力出口,P = 101325 Pa。
3) 司机室壁面边界条件:仪表台、地板、座椅视为绝热。车体(车窗、司机室壁面等)传热系数取为
 (a)
(a)  (b)
(b)
Figure 2. Finite-elements models; (a) Finite-elements model of driver compartment; (b) Finite-elements model of driver, instrument panel and floor
图2. 有限元模型;(a) 司机室有限元模型;(b) 司机、仪表板与地板有限元模型
k = 2.l W/(m2×K)。
4) 将人体视为恒温边界条件,作为固定热源 [12] 。夏季人体散热量为99.08 W/m2,冬季为77.34 W/m2。
5) 太阳辐射选为长春(东经125˚19',北纬43˚43')夏季正常天气下的辐射量。夏季车外环境温度设为35℃,冬季车外环境温度设为−15℃。
4. 数值模拟结果分析
由于RNG k-ε湍流模型可以更好地处理高应变率及流线弯曲程度较大的流动,所以在室内流场模拟和气流组织方面有较高的准确性 [13] ,所以本研究选用RNG k-ε湍流模型作为求解模型进行计算。
依据UIC 651:2002动车设计标准,选取距离地板高1500 mm的截面分析夏季、冬季两种工况下的司机头部附近温度和空气流速。选取距地板、顶板各100 mm处的截面分析夏季、冬季两种工况下司机室的整体温度分布。图3为距离地板上方1500 mm处的温度场仿真结果,图4为距离地板上方1500 mm处的速度场仿真结果(图中圆圈所示区域为司机头部对应位置)。图5为夏季工况下距离地板上方100 mm处和距离顶板下方100 mm处的温度场仿真结果,图6为冬季工况下距离地板上方100 mm处和距离顶板下方100 mm处的温度场仿真结果。
由图3可以看出,夏季工况下司机头部附近温度在21.4℃~22.2℃之间,温差只有0.8℃;冬季工况下司机头部附近温度在22.0℃~23.0℃之间,温差小于2℃。两种工况下整个截面内的空气温度分布比较均匀,说明温度场的分布比较合理。
 (a)
(a) 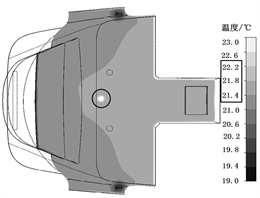 (b)
(b)
Figure 3. Result of temperature simulation 1500 mm above floor; (a) Summer condition; (b) Winter condition
图3. 地板上方1500 mm处的温度场仿真结果;(a) 夏季;(b) 冬季
 (a)
(a)  (b)
(b)
Figure 4. Result of air-flow speed simulation 1500 mm above floor; (a) Summer condition; (b) Winter condition
图4. 地板上方1500 mm处的速度场仿真结果;(a) 夏季;(b) 冬季
 (a)
(a)  (b)
(b)
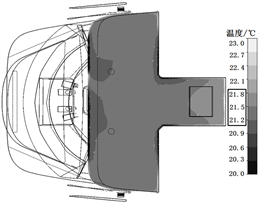
Figure 5. Result of temperature field simulation for summer condition; (a) Temperature distribution near floor; (b) Temperature distribution near roof
图5. 夏季工况下温度场仿真结果;(a) 地板附近温度;(b) 顶板附近温度
 (a)
(a)  (b)
(b)
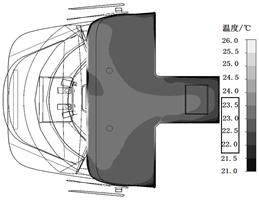
Figure 6. Result of temperature field simulation for winter condition; (a) Temperature distribution near floor; (b) Temperature distribution near roof
图6. 冬季工况下的温度场仿真结果;(a) 地板附近温度;(b) 顶板附近温度
由图4可以看出,夏季工况下头部附近的空气流速在0.10 m/s~0.30 m/s之间,且绝大部分区域都在0.25 m/s之下,司机活动区域的最高风速也没有超过0.50 m/s;冬季工况下,头部附近的空气流速小于0.2 m/s。两种工况下整个截面内的流速分布也比较均匀,说明空气速度场的分布也是比较合理的。
由图5可以看出,夏季工况下地板附近温度在21.5℃~22.1℃之间,顶板附近温度在21.2℃~21.8℃之间,整体温差小于10℃,并且两个截面的温度分布比较均匀。
由图6可以看出,冬季工况下地板附近温度在21.8℃~23.9℃、顶板附近温度分布在22.0℃~23.5℃之间,两个截面的温度分布也比较均匀,温差也小于10℃。由此可见,不管是夏季还是冬季,整个司机室内的温度分布较为均匀,温差最大为1.7℃,符合设计标准要求。
5. 人体热舒适性分析
传统的ASHRAE七点标尺主观评价方法、PMV-PPD评价方法、有效温度评价方法以及标准有效温度(SET)评价指标都是假定人体所处的环境是一个均匀的热环境,适用于建筑室内热舒适的评价。然而汽车车室空间相对狭小、气流速度和梯度较大,太阳辐射不对称,车室内热环境非常不均匀,因此不能当做均匀热环境来看待。因此通常采用当量温度(EQT)和当量均匀温度(EHT)作为评价指标。
上文结合UIC 651:2002标准对司机室的环境变量进行了评价,为全面评价司机的舒适性,需要考虑人体适应因素,本文选择当量温度指标进行分析。计算时,先将人体分段,计算各段与周围环境的热交换,然后利用当量温度指标代替全身热舒适性指标来计算和评价非均匀环境中的人体热舒适性,将计算结果与评价标准进行对比,即可对身体各部位的舒适性进行评价( [1] ,p. 123)。当量温度计算模型为:
(9)
式中:Teq,i为人体第i节段的当量温度;ts,i为人体第i节段皮肤表面温度;vair,i为人体第i节段周围的空气速度;ta,i为人体第i节段周围的空气温度;Si为第i节段的表面积,在CATIA中测量得到;
为斯蒂芬波尔兹曼常数,5.67 × 10-8 W/(m2∙K4);εi为人体第i节段体表的发射率,可取皮肤和服装的平均值0.97;fi,j为人体第i节段对人体j节段的有效辐射区域系数,坐姿情况下可取为0.7;tj为乘员舱内部第j个部件的温度;Qsol为人体得到的太阳辐射;hcal,i为人体第i节段附近空气的对流换热系数,取为8.7 W/(m2∙K)。在Fluent中对模拟计算结果进行测量,其中身体各肢段的环境温度采用取平均值的方法得到。将各参数带入式(9)计算得到夏季、冬季工况下相应部位的当量温度如表2所示。
将计算所得结果与Nilsson舒适模型 [14] 进行对比,绘制成曲线如图7所示,图中的1、2、3和4为四条舒适边界线,边界线之间的区域即为图中对应的热、暖等区域。由图7(a)可以看出,夏季工况下,手部和大

Table 2. Results of equivalent temperatures computation
表2. 当量温度计算结果
 (a)
(a)  (b)
(b)
Figure 7. Valent temperatures calculation results for different body parts; (a) Summer condition; (b) Winter condition
图7. 不同部位的当量温度;(a) 夏季;(b) 冬季
腿的当量温度偏低,其余部分肢体的当量温度在“正常”的舒适区间内。由图7(b)可知,在冬季情况下,大腿部位当量温度稍低,其他肢体部位于“暖”的舒适区间内。对比两图可以看出头部当量温度低于脚部的当量温度,符合“头凉脚暖”的热舒适性准则。综合可知,该司机室的HVAC系统满足人体的热舒适性要求。
6. 结论
1) 由上述分析结果可以看出,在给定送风条件下及夏季和冬季两种工况下,司机头部附近空气温度在21.0℃~23.0℃范围内,空气流速在0.10 m/s~0.30 m/s范围内,整个司机室温差小于1℃,温度和空气流速分布比较均匀,符合UIC 651:2002标准的设计要求。所选动车组司机室HVAC系统的风口尺寸、送风条件以及边界条件设置保证了室内良好的流场分布。
2) 人体热舒适性进行分析的结果表明本HVAC系统满足人体的热舒适性要求。
3) 进风口的布置对司机室的温度场有较大影响,由当量温度的计算结果可以看出,大腿部位较人体其他部位温度低,因此HVAC系统腿部进风口的温度和风速应当适当调节,满足司机整体“头冷脚暖”的舒适性准则。
4) 文中采用的方法能够有效计算动车组司机室的温度场以及速度场,为司机室内部热环境优化提供帮助。
本文从环境变量和人体适应因素角度出发,综合考虑了全身各部位的舒适性,采用当量温度指标对动车组司机室进行了热舒适性分析,有效地弥补了目前相关研究的不足,本文的研究方法以及成果可以为轨道车辆司机室的相关热舒适性分析提供一定的参考。目前的研究在边界条件设定时参考的是已有的研究成果;对于不同企业设计时的相关参数设置,则应根据实际的使用条件设定,这些也有待进一步研究和积累。此外,针对风口参数的影响,未来将对司机室多风口以及不同风口布置位置时的司机室热舒适性进行进一步研究。