1. 引言
当今社会环境问题日益突出,寻求环保可持续能源成为越来越多研究者所关注的重点。质子交换膜(Proton Exchange Membrane, PEM)电解池技术是通过电解水制氢,产生的氢能可以作为清洁能源加以使用。在电解池的阳极和阴极发生的电化学反应方程式如下:
阳极:
阴极:
总反应式:
PEM电解池的反应物和生成物均对环境无污染,同时还具有启动速度快、可再生、电流密度高等优点,使其具有广泛的应用前景 [1] [2] 。此外,电解池与燃料电池组合而成的一体式再生燃料电池因其具有很高的比能量和比功率,在民用、航空航天及偏远地区的储能系统等领域内得到了较为广泛的应用 [3] [4] [5] 。
目前,国内外对PEM电解池两相数值模拟研究的文献相当有限。王昭毅 [6] 建立了三维、两相、等温、瞬态的PEM电解池阳极侧的数学模型,研究了阳极氧气浓度的分布和水浓度的分布规律。同时模型也探究了不同电流密度下、不同液态水进口流速时对氧气和液态水分布的影响。赵金刚 [7] 应用VOF模型对电解池点状流场内气液两相的流动进行了数值模拟。模型的计算区域包括点状流场、多孔介质扩散层。作者利用该模型主要研究了进口形状、电流密度、进口流速等工况下,流场内气液两相流动的规律。Nie等人 [8] 采用混合物模型的方法建立了PEM电解池阳极侧流场板内三维、两相、等温的数学模型。模型主要研究了流场板内气液两相的流动特征,从而为电解池的设计提供有效的指导。Han等人 [9] 基于多孔介质流动理论和电化学之间的关系建立了PEM电解池气体扩散层内两相传输数学模型,研究了气体扩散层内的传输性质及对PEM电解池电压和效率的影响。Aubras等人 [10] 建立了二维、垂直流道方向的PEM电解池稳态模型,模型将催化层考虑为没有厚度的界面,求解了膜电极内的传热、传质和电荷守恒。模拟的结果表明,欧姆阻抗的降低能够提高PEM电解池的效率,且气泡的聚结现象与传质的改善相关。基于上述对电解池两相数值模拟的文献研究发现,电解池两相数值模拟的研究相对较少,研究的内容比较有限,且很少有文献去分析电解池内部的温度分布规律。
本文拟建立沿流道方向的二维、两相、瞬态、传热传质及耦合电化学反应的全电池数学模型,研究PEM电解池内部的气液两相分布规律,温度的变化规律及电化学的瞬态响应规律。
2. 模型描述
2.1. 模型的计算区域及假设
本文针对质子交换膜电解池建立了二维、两相、非等温、瞬态及耦合电化学反应的数学模型。图1显示的是PEM电解池的结构示意图。二维模型的计算区域如图2所示,包括氧电极侧气体流道、气体扩散层、催化层,氢电极侧气体流道、气体扩散层、催化层,及基于PEM的电解质膜。流道左侧均为入口,右侧均为出口。
为了简化上述模型,对模型进行了以下假设:1) 在入口流速范围内,由于雷诺数较小,流动状态为层流 [6] ;2) 各层之间接触热阻忽略不计 [11] ;3) 质子交换膜对气体组分不可渗透 [12] ;4) 多孔介质均为各相同性 [6] ;5) 重力的影响忽略不计 [11] ;6) 所有的气体组分为不可压缩的理想气体 [6] 。
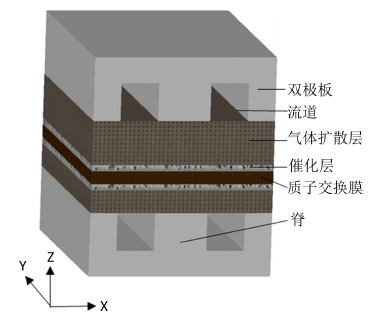
Figure 1. Schematic diagram of a PEM electrolyzer cell
图1. PEM电解池的结构示意图

Figure 2. Computational domain of 2D model
图2. 二维模型的计算区域
2.2. 控制方程
2.2.1. 电荷守恒
基于欧姆定律,多孔电极内电子的传输及质子交换膜内质子的传输方程如下:
(1)
(2)
式中,
和
分别是电子电势和电解质电势,
和
分别是有效的电子电导率和电解质电导率。对于各向同性的多孔介质,
;对于质子交换膜,
。源项
和
是与催化层内体电流密度相关。在阴极催化层内,
和
;在阳极催化层内,
和
;
和
分别是阴极和阳极的体交换电流密度,可以用Bulter-Volmer方程计算如下:
(3)
(4)
式中,
是活化比表面积,
是参考交换电流密度。
和
分别是阴极和阳极的过电势,可用如下公式进行计算:
(5)
(6)
式中,
是平衡电势,可用下式进行计算 [13] :
(7)
2.2.2. 质量和动量的守恒
对于气体组分,描述其质量和动量守恒的方程如下:
(8)
(9)
式中,
是气体混合物的密度,
是气体混合物的速度矢量,
是气体组分有效的孔隙率,其与材料的固有孔隙率和液态水的饱和度有关,可表示为:
(10)
2.2.3. 组分守恒
运用Maxwell-Stefan方程来描述气体组分的对流和扩散,方程如下:
(11)
(12)
 (13)
(13)
式中,
是组分
的质量分数,
是组分
的摩尔分数,
是气体组分有效的扩散系数,可通过Bruggemann’s方程进行修正。
是二元气体组分的扩散系数。
2.2.4. 液态水传输的守恒方程
液态水的连续性方程为:
(14)
式中,
是液态水的密度。由于液态水在电解池内部的传输是靠毛细压力所驱动的,描述电解池内部毛细压力的经验公式 [9] 可被表示为:
(15)
式中,
和
分别是液压和气压,可通过达西定律进行求解,表达式如下:
(16)
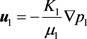 (17)
(17)
(18)
(19)
(20)
联立方程(14)~(17),最终可得求解液态水饱和度的控制方程为:
(21)
式中,
是多孔材料的接触角,
是多孔介质的固有渗透率。
是液态水饱和度,被定义为液态水体积与多孔介质体积之比。
是表示液态水与水蒸气之间相变的源项,用以下公式表示:
(22)
式中,
和
分别是冷凝系数和蒸发系数,
是水蒸气的摩尔分数,
是水蒸气的饱和压力,可用下述公式进行计算:
(23)
2.2.5. 能量守恒方程
通过假设所有的相都处于热平衡,能量守恒方程可被表示如下:
(24)
式中,
和
分别是比热容和有效的导热系数,下标
分别表示气相、液相和固相。在多孔介质内,
和
可用下式进行计算求解,
(25)
(26)
式中,
分别是液态水的导热系数、气体的导热系数和多孔的固体介质的导热系数。阳极气体扩散层的材料为钛网,阴极气体扩散层的材料为碳纸,它们各自的导热系数被列于表1中。
是热源,包括了可逆的电化学反应热,不可逆热,欧姆热和相变潜热。

Table 1. Physical parameters and basic conditions in this model
表1. 模型中的物理参数和基本条件
2.3. 初始条件和边界条件
模型的初始条件为:电池的温度为353.15 K,阳极液态水饱和度为0.2,操作压力为1 atm;阴极侧的电子电势和电解质电势分别为:
和
;阳极侧的电子电势和电解质电势分别是:
和
。边界条件为:阳极流道入口处给定液态水饱和度为0.2,温度为353.15 K;阳极、阴极入口处均给定水蒸气质量分数为1,平均速度为0.3 m/s;阳极、阴极出口处给定压力为1 atm;阳极、阴极流道与气体扩散层界面处给定电势为
。
2.4. 网格划分和模型验证
本文模型采用的是有限元法对前面所描述的控制方程进行离散化求解。模型的收敛条件设置为连续两次迭代之间,所有变量的相对残差均小于10−5。单元的数量对模型的计算结果会产生影响。倘若单元数过小,将会导致模拟计算出来的结果误差较大;单元数过大,又将会增加模拟的计算量。因此,选择一个合适的单元数既能提高模拟计算的精度,又能减少模拟计算量。本文选取电压为1.8 V时,电解池的电流密度作为单元数无关性验证的指标。模型共选取了七组单元数,通过分析,当单元数超过22,000时,单元数的增加对模拟计算的结果几乎没有影响,因此本文模型选取的单元数为22,000。此外,本文还利用文献中的实验数据 [14] 对本文模型进行了验证,验证的结果如图3所示。从图中可以看出,模型验证的结果与实验数据吻合较好。
3. 结果分析与讨论
图4展示的是位于阳极催化层中心点处,液态水饱和度、温度、电流密度、氧气质量分数随时间的瞬态响应。从图中可以看出,电解池模式下,阳极催化层中心点处液态水饱和度随着时间的增加而逐渐的减小,最终到达稳态。因为电解池模式下反应物为液态水,液态水在该过程中不断的被消耗。液态水由瞬态到达稳态这一过程中所需要的时间大约为10 s。而温度则随着时间的增大先急剧的减小,之后又缓慢上升而趋于稳定,电流密度的在该过程中的变化趋势则与温度相同。温度由瞬态到达稳态所需要的
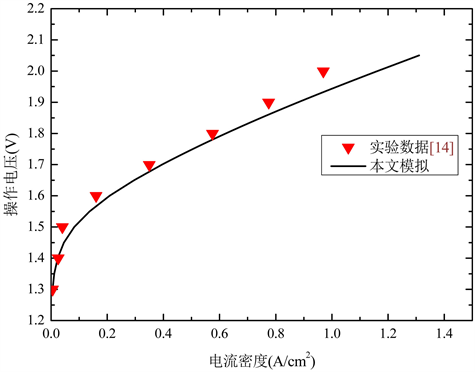
Figure 3. Comparison of the simulated PEM electrolyzer cell performance and the experimental data [14] , T = 363.15 K
图3. 模拟计算的电解池性能与实验数据之间的对比,T = 363.15 K
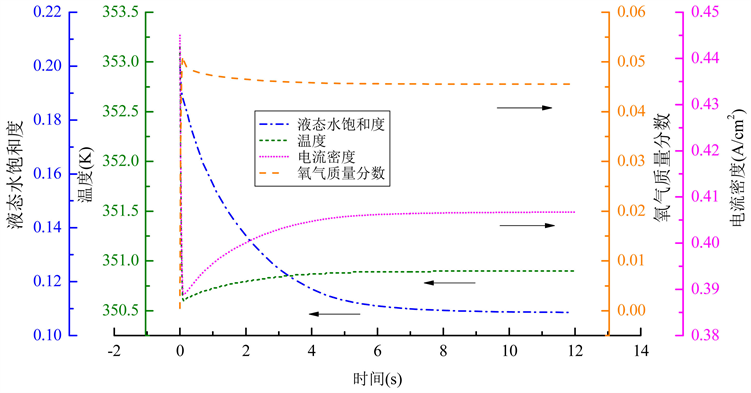
Figure 4. Dynamic responses of relevant parameters in the central point of the anode catalyst layer
图4. 阳极催化层中心点处相关参数的瞬态响应
时间大约为6 s。因为电解池模式刚开始时,电池的工作电流密度较大,电化学反应速率较快。因此,电化学反应所需要吸收的热量就较多,电池的温度出现了急剧的下降。同理,之后由于电流密度的回升,导致温度也出现了缓慢上升的趋势。氧气质量分数则随着时间的增加而迅速的增大,最终也到达稳态。因为在电解池模式下,电解液态水产生氧气,因此氧气的质量分数会增大。电流密度和氧气质量分数从瞬态到达稳态的时间大致与温度相同。液态水饱和度从瞬态到达稳态的时间较温度、电流密度和氧气质量分数到达稳态的时间长。
图5是电解池阳极流道、阳极气体扩散层、阳极催化层内液态水平均饱和度随时间的瞬态响应。从图中可以看出,在电解池模式下,各层液态水平均饱和度均随着时间的增加而逐渐的减小,最终趋于稳态的过程。因为电解池模式下液态水存在阳极侧每一层中,液态水随着时间的增加不断的被电解,导致各层液态水的含量随时间逐渐减小。其中,催化层内液态水平均饱和度随时间的变化梯度最大,而流道内液态水平均饱和度随时间的变化梯度最小。原因是电化学反应发生在催化层内,液态水在该处被消耗,因此催化层内液态水平均饱和度变化梯度是最大的。液态水平均饱和度在沿着阳极流道至催化层方向是逐渐减小的。因为流道内液态水的浓度始终高于气体扩散层和催化层,液态水是沿着流道至气体扩散层方向逐渐递减,加上催化层内的电化学反应,导致催化层内的液态水饱和度值较其他两层而言相对较小。
图6所示是在四个不同时刻下,液态水饱和度沿着A-A截面(距流道进口四分之一的截面)和C-C截面(距流道出口四分之一的截面)的分布。从图中可以看出,沿着A-A截面和C-C截面,液态水饱和度在0.02 s时的变化梯度均较小,在5 s时的变化梯度均较大。因为在0.02 s时电解池的工作电流密度低于5 s时的工作电流密度。电流密度越大,液态水的消耗量就越多,变化的梯度也越大。液态水饱和度沿A-A截面和C-C截面减小的梯度随着时间的增加也在逐渐增大。沿着A-A截面至C-C截面方向,液态水饱和度逐渐减小,且C-C截面液态水饱和度随时间的变化梯度较A-A截面的变化梯度大。原因是在电解池模式下,液态水涌入到流道内,由于浓差驱动,液态水在垂直流道方向通过对流和扩散到达气体扩散层和催化层。液态水在沿着流道方向从进口到出口逐渐减小,出口处的液态水饱和度值较低。
图7则是在不同时刻下,沿着B-B截面(流道的中心截面)的温度分布。从图中可以看出,在上述四
个时刻下,B-B截面各层的温度均低于电池的初始温度,说明在电解池模式下,电池内部总体表现为吸热反应,电池的总体温度是下降的。分析原因为电解池模式下,电解液态水所需要吸收的电化学反应热大于电池所产生的焦耳热。阳极区域内的温度变化梯度较阴极区域内温度的变化梯度大,主要是因为电解液态水的反应区域在阳极的催化层。比较上述四个时刻,在0.1 s时电池的最低温度值要低于其他三个时刻的最低温度值。原因是,在0.1 s时,电池的电流密度相比于其他三个时刻要小,电池所产生的焦耳热较少。电解池模式在上述四个时刻下,电池的最低温度均位于阳极催化层与质子交换膜交界面上。
在0.02 s,0. 1s,0.5 s,1 s四个时刻下,沿着流动方向,催化层中心线上电流密度的值是逐渐减小的(见图8)。
图5. 各层液态水平均饱和度随时间的瞬态响应
图6. 不同时刻,液态水饱和度沿A-A截面和C-C截面的分布
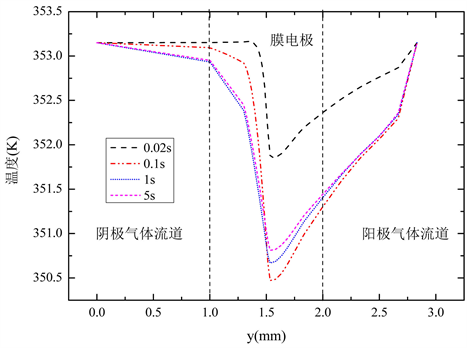
Figure 7. Temperature distribution along line B-B at different times
图7. 不同时刻,沿B-B截面的温度分布

Figure 8. Current density distribution along the catalyst layer central line at different times
图8. 不同时刻下,催化层中心线上电流密度的分布
在0.02 s时,电流密度减小的幅度最小,而在0.1 s时电流密度减小的幅度最大。随着时间的推移,催化层中心线上电流密度降低的幅度由起初的最小,转变为先增大后减小的趋势。分析原因是电解池模式刚开始时,液态水的浓度较高,电流密度的值较高。随着电解反应的进行,液态水逐渐被消耗,浓度降低,使反应速率有所下降,电流密度的值从而减小。
图9所示为在0.02 s,0.1 s,1 s,5 s四个时刻,氢气质量分数沿着A-A截面(距流道进口四分之一的截面)和C-C截面(距流道出口四分之一的截面)的分布。从图中可以看出,随着时间的增加,氢气质量分数沿着A-A截面和C-C截面的变化梯度均在逐渐的减小。沿C-C截面氢气质量分数随时间的变化梯度较A-A截面的变化梯度大。氢气质量分数均沿着A-A截面至C-C截面方向逐渐增大,且沿着气体流道至催
化层方向是逐渐增加的,在催化层内氢气的质量分数最大。原因是在催化层内发生电化学反应产生氢气,所以氢气在该处的浓度最大。
从图10中可以看出,电解池模式开始时,电池总体的反应为吸热反应,各层的平均温度在1 s内迅速下降到最小值。之后随着反应的进行,各层的平均温度又出现略微升高的趋势。这种趋势在催化层内表现的最为明显。温度的变化率由最初的较大转变为逐渐减小。原因是电解池模式开始时,电池电化学反应速率较快,所需要吸收的热量较多,因此电池的温度急剧下降。随着电化学反应速率的下降,电池所需要吸收的热量下降,由于活化极化热和欧姆热的存在,导致电池的温度会有所升高,但仍然低于电池的工作温度。
图9. 不同时刻,氢气质量分数沿A-A截面和C-C截面的分布
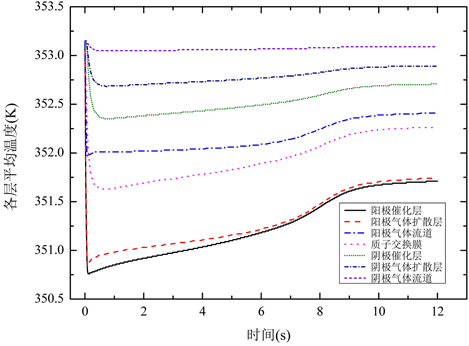
Figure 10. Transient responses of the average temperature in different layers
图10. 各层平均温度随时间的瞬态响应
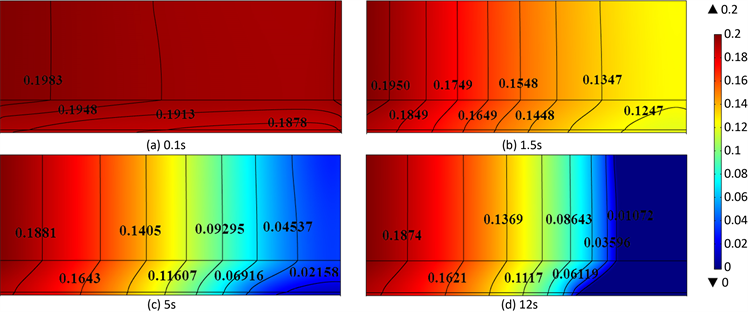
Figure 11. Transient responses of the average temperature in different layers
图11. 各层平均温度随时间的瞬态响应
在四个不同的时刻下,液态水饱和度分布云图(见图11)。从图中可以看出,沿着流道入口到出口方向,液态水饱和度在逐渐减小。液态水饱和度在沿着流道至催化层方向也是逐渐递减的,且在催化层中液态水饱和度值最小。原因是催化层内液态水被电解,导致该处的液态水浓度较低。液态水在多孔的催化层和气体扩散层内的变化梯度较流道内的变化梯度大。原因是多孔介质的渗透率和孔隙率比流道小的多,在多孔介质内的压力变化梯度较大。且随着时间的增加,液态水饱和度在各层中的分布是逐渐减小的。
4. 结论
本文通过建立二维质子交换膜电解池两相、瞬态、传热传质及耦合电化学反应的模型,分析了电解池内部液态水、气体组分、温度、电流密度的瞬态响应规律,从而得到如下结论:
1) 液态水饱和度、温度、电流密度、质量分数的瞬态响应规律是不同的;液态水从瞬态到达稳态的时间较温度、电流密度、质量分数到达稳态的时间长。
2) 液态水在多孔介质内的变化梯度较流道内的变化梯度大;靠近流道入口处截面上,液态水饱和度的变化梯度较出口处截面上的变化梯度小。液态水饱和度在沿流道进口至出口方向和气体流道至催化层方向均逐渐减小,且在催化层内液态水饱和度值最小。
3) 电解池的总体温度是下降的,且电池的最低温度始终出现在阳极催化层中;阳极区域内温度的变化梯度较阴极区域内温度的变化梯度大。电池的最低温度在0.1 s时出现了最小值,此时电池的总体温度降低了3 K左右。
4) 氢气质量分数在靠近流道入口处截面上的变化梯度较出口处截面上的变化梯度小;氢气质量分数沿流道进口至出口方向和气体流道至催化层方向均逐渐增大,且在催化层内氢气质量分数最大。
基金项目
国家自然科学基金项目(51476003)。