1. 引言
PM2.5是指悬浮在空气中粒径小于等于 2.5 μm的细小颗粒物。目前,以PM2.5为代表的大气污染已经成为造成全球疾病负担最重要的环境因素之一[1]。环境中PM2.5的暴露对人群造成的健康风险研究成为流行病学的一大热点研究问题。其中,PM2.5浓度的时空分布模拟是其健康风险效应分析的基础[2]。PM2.5的空间分布方法有基于监测站点的最近距离法,遥感卫星数据反演法,空气质量模型法和土地利用回归法(Land use regression, LUR)等,但都存在一些不足之处导致在模拟过程中存在一些不可避免的偏差和限制[3] [4] [5]。
1997年,Briggs等人在小区域空气质量与健康效应(SAVIAH)的研究中首次提出基于回归算法的LUR模型,并之后广泛应用于城市内部的大气污染物分布模拟[6]。近年来,部分研究结合卫星遥感数据,利用LUR方法成功模拟出国家乃至全球Andrew等人成功用LUR模型模拟出全球尺度的NOx分布[7]。尺度的污染物时空分布,例如Matthew等人总结了21个大区域尺度的LUR模型应用[8];模拟出欧洲,美国,加拿大,澳大利亚等地的大气污染物分布。Luke等人开展独立采样实验证明了国家尺度的LUR模型的有效性[9]。
尽管许多研究表明大气污染物在城市内部之间的差异比城市之间的差异更加显著[10],这也是LUR方法主要应用于小范围模拟的重要原因[6],但这一特点并不适用于具有高背景浓度的中国地区。中国是世界上人口最多的国家,在过去几十年的经济飞速增长中,造成了如雾霾等许多环境问题。[11]Geng等人计算得到中国的人口加权PM2.5浓度为71 μg/m3 [12],远超过WHO的第一阶段目标35 μg/m3。部分经济集中区,如京津冀长三角等地,形成了较为集中的污染区,这一特点使得中国地区之间的差异相对城市内部间的差异更加显著。许多国家的背景浓度较低,造成了城市内部之间的浓度变化显著。并且PM2.5是二次污染物[13],与NOx不同,其空间分布会在更大空间尺度上受到影响,在大范围研究中则更能体现出空间变化。在这种情况下,利用LUR方法对全国的PM2.5浓度分布则更加适合,而相关研究未见报道。
因此,本文基于遥感卫星的反演数据和LUR方法的耦合模型,对2013~2015年中国的PM2.5浓度的时空分布进行模拟,为后续中国的PM2.5健康效应分析提供污染物暴露依据。
2. 数据和方法
2.1. PM2.5监测数据
本研究的PM2.5监测数据来源于环保部环境监测总站空气质量实时发布系统,时间范围为2013年1月到2015年12月,仅保留缺失数据量低于25%的站点,并计算各个站点的年均浓度。表1显示了最终进入模型的PM2.5监测浓度的样本数据。我国的空气质量监测网从2013年开始建立,2013年和2015年的有效样本量为477个和928个,可见在3年时间中,监测站点数量得到了飞快的增长。同时,PM2.5的平均值从2013年的72.917 μg/m3下降到2015年的52.754 μg/m3,可见随着国家对于空气污染问题的治理力度逐渐增大,PM2.5年均浓度呈现较为显著的下降趋势。在后续的研究过程中考虑到所选年份之间的差异,通过引入时间因子作为LUR模型的输入变量,即2013年为−1,2014年为0,2015年为1。
2.2. 预测变量
本研究所用地理要素变量可以分为地理位置、排放清单、遥感卫星数据、道路、社会经济指标、土地利用和气象条件,其中道路和土地利用数据利用各个站点的不同大小的缓冲区提取。根据之前的相关研究,选择的缓冲区半径有100 m, 200 m, 300 m, 400 m, 500 m, 600 m, 700 m, 800 m, 1000 m, 1200 m, 1500 m, 1800 m, 2000 m, 2500 m, 3000 m, 3500 m, 4000 m, 5000 m, 6000 m, 7000 m, 8000 m和10000 m这22个缓冲区。
地理位置数据包括各个监测站点的经纬度和海拔。排放清单数据来源于中国多尺度排放清单模型MEIC (http://www.meicmodel.org/),因为其最高分辨率为0.25度(~25 km),远远大于缓冲区半径,因此对于排放清单数据使用所在位置点提取污染物排放量。遥感卫星数据反演模拟来自Donkelaar等人的全球PM2.5数据库的研究成果[14],根据以前的研究,本文所采用的较为粗糙的0.1˚*0.1˚并且没有经过地面校正的数据,避免站点数据的重复计算[15]。全国道路网来自于;相关社会经济数据来源于中国科学院资源环境科学数据中心(http://www.resdc.cn/),其中全国GDP/人口密度空间分布公里网格数据是在全国分县GDP/人口统计数据的基础上,考虑GDP/人口–自然要素的地理分异规律,通过空间插值生成的1 km*1 km栅格数据;夜间灯光数据通过DMSP极轨卫星项目,通过线性扫描业务系统(OLS)得到,其广泛用于社会经济因子和其他环境能源领域。土地利用数据来源于2015年中国1:10万比例尺土地利用现状遥感监测数据库数据集,基于landsat 8遥感影像,通过人工目视解译生成。本研究选用耕地、林地、草地、水域、居民地,未利用6个一级类型在各个缓冲区内的类型面积的百分比作为模型的输入。气象数据来源于中国气象网发布的实时气象数据(http://data.cma.cn/),提取气象站点的温度、降雨量、风速、相对湿度、日照等数据,仅保留缺失数据量低于25%的站点,最终保留839个站点数据,考虑到气象因素随空间变化的条件较为连续,并且气象站点和空气质量监测站点并不重合,因此本研究通过克里金插值的方法得到全国的气象条件分布图,再通过空气质量监测站点位置进行提取相关气象条件。由于使用不同半径的缓冲区进行处理,最终得到的预测变量有213个。预测变量的具体情况如表2所示。

Table 2. Predictive variable information
表2. 预测变量信息统计
2.3. 模型的建立与检验
Knibbs和Andrew等人[7] [16]在研究大尺度LUR模型中采用了Lasso和逐步多元回归结合的方法。Lasso法首次由Tibshirani Robert 在1996年提出[17],通过构造惩罚函数,使得它一些系数得到压缩,是一种处理具有复共线性数据的有偏估计方法。由于本研究中LUR模型的预测变量达到213个,并且由于大量缓冲区的存在变量之间存在着较强的共线性,因此采用这种有偏估计可以达到很好选择变量的效果。逐步多元回归是LUR模型的经典算法[18],根据相应方式和准则确定最后的模型的变量和参数。另外,由于卫星遥感数据在大尺度LUR模拟中发挥着越来越大的作用,本研究分别探究存在遥感信息和不加入遥感数据两类模型。
其具体步骤如下:首先,因为lasso法不适用处理纵向数据,因此分别对3年的数据lasso法的变量筛选,在任意一年中得到保留的变量则进入下一步。接着用逐步多元回归法进行模型的建立:模型1强制加入卫星数据,模型2不加卫星数据;显著性水平为5%;加入先验条件(例如部分变量需要符合确定的正负效应关系,PM2.5的值最低为0等);当一个变量能够通过显著性t检验,并且能够增加模型的调整R2在1%以上,才能够得到保留。
模型的表现和检验采用十折交叉验证法,将数据分成10份,其中1份作为测试数据,另外9份作为训练数据,重复多次建立模型,从而得到模型的R2,调整R2,绝对偏差和百分比偏差。
在完成模型的建立后,对全国区域建立5 km*5 km网格,并以每个网格的中心点为准,提取其相关地理信息变量,输入模型中计算该点的PM2.5浓度预测值。最后将该点的值赋予整个网格,完成全国连续三年的PM2.5浓度分布图。
3. 结果与讨论
3.1. 模型的建立
本研究分别对带有卫星遥感数据和不具有卫星遥感数据两种情况进行模型的构建,最后模型的参数全部通过显著性检验,并且方差膨胀因子均小于5。最终两类模型的参数和表现可参见表3。
比较两类模型可知,模型1的拟合度R2为0.7,模型2的拟合度R2为0.53,有较为明显的提升,从而证明了卫星遥感数据在模拟大范围PM2.5时空分布的重要意义。Beckerman等人也完成过对于非卫星遥感数据和有遥感数据模型的比较,其中的normR2分别是0.09和0.54,差异更加明显。因此可以看到尽管卫星遥感数据发挥了非常重要的作用,但是模型对于遥感卫星数据的依赖度并不是特别高,从而能够更好地发挥出各种地理要素和LUR方法的优势。
两类模型的形式也有一些相似之处和不同之处。同时进入两类模型的参数有城乡工矿面积占比,降水和年份。可见这三类地理信息要素在LUR模型构建的重要性。并且三个参数在两类模型中的正负作用是相同的。值得注意的有:年份作为时间因子加入模型中,很好地反映出3年中PM2.5浓度较为明显的下降趋势,在模型中产生了较为明显的影响;模型1中存在5个气象变量;模型2中存在2个气象变量,除了气温外的气象变量均有体现,说明在大尺度的PM2.5年均分布中与各地的气象条件存在着较为密切的关系。不过在两类模型中,道路因素、社会经济等变量均没有出现,一方面可能是由于在大尺度区域
1减少R2代表排除出这一变量后模型的R2降低的值。
中PM2.5的分布可能受到具体道路等指标影响较小,另一方面也是由于地理信息数据的可获取度以及精度所致。
后续将选择模型1作为本研究的PM2.5空间分布模型。模型1共有7个变量,上述已经提到,其中气象条件变量占据5个。其中除了气压是正效应外,其他变量如风速、降雨、气压和相对湿度等均是负效应。其中卫星反演数据的减少R2最大,可见其在模型中发挥着非常重要的作用。而6000米缓冲区内的城乡工矿占比也加入到模型,并对PM2.5具有正效应。
3.2. 模型的检验
图1(a)和图1(b)表示了通过十折交叉验证得到的PM2.5的预测值和实际值的结果。
可见图中的所有点均较为集中地分布在Y=X的两侧,说明模型的可靠度。对模型1和模型2进行比较,模型1相对于模型2的点更加集中在直线的两侧,因此其具有更好的可靠度。如果对于不同年份来讲,2014年和2015年表现较好,但大部分离群点主要是2013年,并且这些离群点大部分是观测值大于预测值,即存在低估。这一现象可能有如下几点原因造成:进入模型的2013年监测点位较少,因此在训练模型中可能对于拟合该年的部分相对较弱;另一原因是2013年整体PM2.5浓度偏高,并且存在一些较为极端的高点,由于这一特点反映在全样本中占据很少的一部分,因此无法在模型中得到体现。
3.3. 模型的应用
利用上述模型1在全国区域建立网格,从而绘制出连续三年的PM2.5分布图。如图2、图3、图4。通过纵向比较,随着时间推移,PM2.5的最大浓度值也在逐年降低。但是PM2.5的空间分布随年份的变化并不显著。可见PM2.5的空间分布规律基本类似。
PM2.5的浓度分布从10 μg/m3左右到120 μg/m3均有分布,可见其空间差异度非常明显。从图中可见,京津冀地区,长三角地区,华中城市群和成渝城市群形成PM2.5高浓度区域。说明中国PM2.5问题与飞速发展的经济有十分密切的关系。在这些工业和人口聚集地中,排放大量的污染物,从而造成较为严重的PM2.5问题。WHO对第一阶段达到的PM2.5目标为年均35 μg/m3,而这些地方远远超过了这一标准,可见中国的PM2.5治理还有较远的距离。另外一个PM2.5高浓度聚集地处于新疆地区,这一部分主要是由于大量的沙漠扬尘所致。
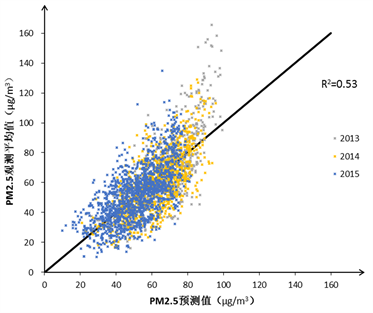
Figure 1. cross-validation prediction of LUR with and without remote sensing
图1. 两类模型交叉验证的结果对比(左图模型1,右图模型2)
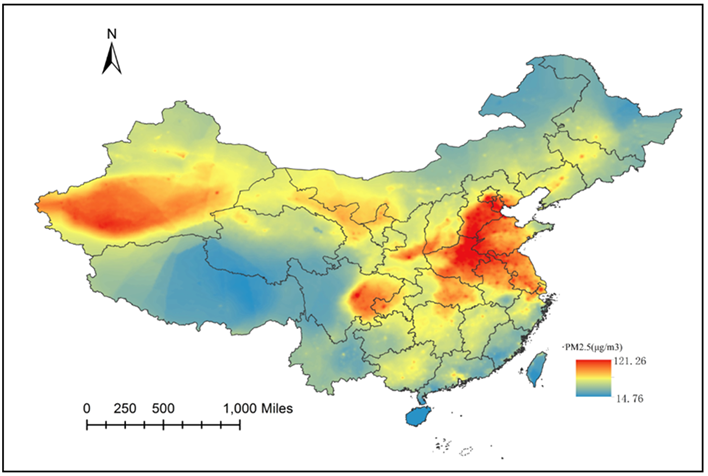
Figure 2. Average PM2.5 concentration predicted in China in 2013
图2. 2013年中国PM2.5分布预测图

Figure 3. Average PM2.5 concentration predicted in China in 2014
图3. 2014年中国PM2.5分布预测图
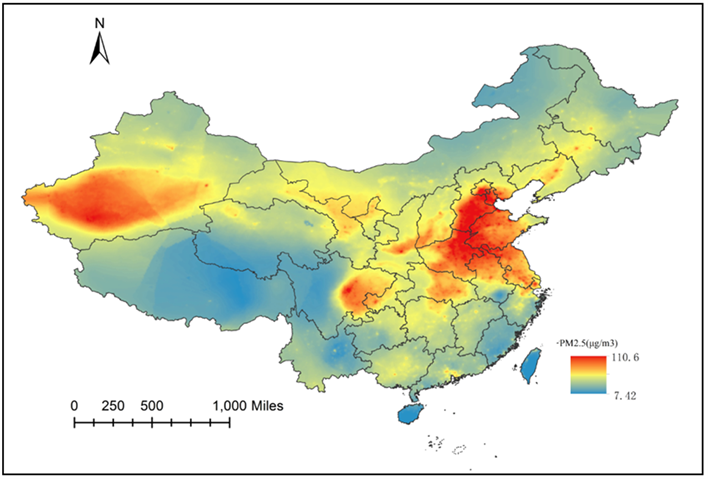
Figure 4. Average PM2.5 concentration predicted in China in 2015
图4. 2015年中国PM2.5分布预测图
3.4. 总结与思考
本研究基于LUR方法的框架,引入卫星遥感数据,模拟出中国2013年到2015年PM2.5浓度空间分布。模型的变量包括5类气象因子及土地利用类型和年份的时间因子,最终模型的R2为0.70。绘制出高精度的中国PM2.5浓度分布图,为后续研究中国PM2.5健康影响提供污染物暴露依据。
NOTES
*通讯作者。