1. 引言
引汉济渭调水工程由“两库、两电、两泵、一洞两段和一网”组成 [1] ,其中“两库”分别为黄金峡水库和三河口水库(简称“黄三”),“两电”分别为黄金峡水电站和三河口水电站,“两泵”分别为黄金峡泵站和三河口泵站,“一洞两段”为秦岭输水隧洞由黄三段和越岭段组成,“一网”为宝鸡至渭南的关中整体调水管网。引汉济渭调水工程正处于建设的重要阶段。截至2017年12月中旬,三河口水利枢纽大坝已浇筑50 m。
关于引汉济渭水资源调配的研究取得了许多成果。曹正浩 [2] 等考虑库区上游规划年用水、坝址下游以及南水北调中线一期工程、汉江中下游的用水要求,引汉济渭工程近期从汉江可引水量为10亿m3,验证了规划可行性。杨晓如 [3] 等基于系统分析方法建立了大系统分解协调模型,以调水区综合效益最大、缺水量最小为全局最优解,得到了2020年和2030年调水量的优化配置方案。苏丹 [4] 等通过建立多目标模型对受水区的水资源进行了优化配置。师小雨 [5] 等对水量分配设置了多种方案进行分析,得到了较为稳定和优越的配水方案。目前,已取得的研究成果大多是关于黄金峡水库和三河口水库联合调度的水资源优化配置,缺乏工程运行初期三河口单一水库调度的研究,主要原因是引汉济渭的设计数据均是在黄金峡水库和三河口水库联合调度的基础上开展的,且黄金峡水库和三河口水库联合调度综合效益显著。然而,随着三河口水库大坝浇筑速度的加快,针对汉济渭初期运行的研究显得愈加重要和紧迫。工程运行初期三河口单一水库如何满足工程初期配水5亿m3的要求,三河口水库的调水潜力如何等问题成为目前亟需解决的关键技术问题。鉴于此,本文建立了三河口单一水库的多目标模型,旨在揭示工程运行初期三河口单一水库的调度规律,探究三河口调水潜力以及发电与调水的转化关系。研究成果对于引汉济渭工程运行初期的水库运行、水资源利用效率和工程效益的发挥具有重要的技术指导意义。
2. 研究区域概况
引汉济渭调水工程作为统筹陕西省三大区域,联通汉江、渭河南北两大水系,构建关中地区大水网的关键性调水工程 [6] ,主要由黄金峡水利枢纽、三河口水利枢纽和秦岭输水隧洞(黄三段和越岭段)三部分组成。其中三河口水利枢纽坝址位于子午河三河口以下约2 km处,控制流域面积2186 km2,占全流域的72.6%。三河口水利枢纽由大坝(坝身设泄洪放空系统)、坝后引水系统、抽水发电厂房和连接洞等组成。水库运行机制为:入口径流经水库调节的泄放流量,首先用于坝后电站发电,随后依次用于满足最小生态基流和供水,当供水能力超过输水能力时,富余的水补充河道用水。工程对应的节点图如图1,三水库多年平均入库径流过程如图2所示。
3. 多目标优化调度模型的建立与求解
3.1. 多目标优化调度模型的建立
三河口水库首要目标是调水,其次是发电。在追求发电量最大时,需要通过存蓄来水抬升水位,导致时段
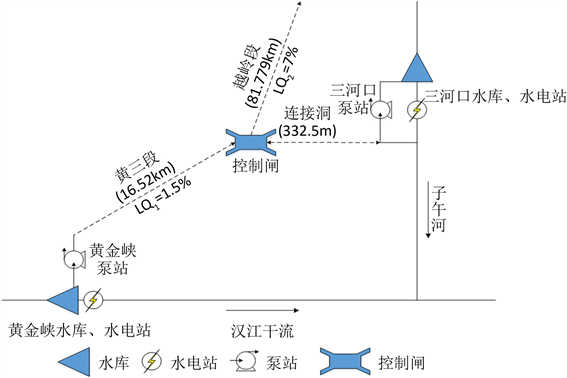
Figure 1. Diversion area node generalization of the project
图1. 工程调水区节点概化

Figure 2. Multi-year average inflow of Sanhekou reservoir
图2. 三河口水库多年平均入库过程
泄放流量减少,引起调水量减少。因此三河口水库发电量和调水量在一定条件下构成竞争关系。本文选取调水量最大和发电量最大作为目标函数,表示如下。
(1)
式中:
表示水库调水量,亿m3;
表示水库发电量,亿kW·h;
表示第
时段调水流量,m3/s;
表示第
调水时段大小,s;
表示第
时段三河口水电站出力,MW;
表示出力系数的大小;
表示第
时段发电流量,m3/s;
表示第
时段发电水头,m;
表示第
时段发电时段大小,s。
3.2. 约束条件
模型的约束条件包括水量平衡约束、水位约束、水电站设备容量约束和流量约束等。
1) 水库水量平衡状态方程
(2)
2) 水库水位约束
(3)
3) 水电站设备容量约束
(4)
4) 流量约束
(5)
式中:
、
分别表示第t时段初和时段末水库库存水量,亿m3;
和
分别表示第
时段水库的入库流量和下泄流量,m3/s;
表示时段水库渗漏和蒸发等损失水量,亿m3;
表示时段大小,s;
和
分别表示第t时段最高和最低限制水位,m;
和
分别表示分水电站t时段的最大和最小出力,MW;
和
表示水电站第m项(水轮机过机、下泄、输水管道等),第t时段允许的最大和最小流量,m3/s。
3.3. NSGA-II求解算法
水库多目标调度研究作为水库调度的热门研究方向,目前形成了许多算法,包括非支配邻域免疫算法、多目标粒子群优化算法、模拟退火算法和非支配排序遗传算法等。其中非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm II, NSGA-II) [7] [8] [9] 因其强大的计算能力和良好的收敛性能而被广泛用于求解水利枢纽的多目标问题,并取得了丰硕的研究成果。因此,本文引入NSGA-II求解模型,计算步骤如下 [10] :
1) 算法参数和变量范围输入,包括选择、交叉和变异概率,种群规模,水库水位边界条件等;
2) 选取水位作为决策变量对个体进行编码,每个个体由三河口水库各时段水位构成,随机产生满足水位,出力和水量平衡等约束的初始种群
;然后对
进行非劣排序并赋秩于每个个体,其中非劣排序以每个个体的调水量和发电量这两个目标函数进行;再对
进行遗传操作,包括选择、交叉和变异,得到新种群
,同时使
;
3) 将父代种群
和子代种群
合并后形成种群
,对
进行非劣操作,以获得非劣前端
;
4) 对所有
按拥挤度距离进行排序,并按锦标赛法选取最好的N(种群规模)个个体生成新的种群
;
5) 对种群
执行遗传操作,形成新种群
,直至达到最大进化代数停止,否则令
并转到(3)。
4. 基于NSGA-II的多目标调度结果与分析
4.1. 数据收集与参数设置
本文收集到三河口水库1954年6月至2010年7月共56年月径流资料和三河口水利枢纽工程的设计资料。经检验,所有资料均满足一致性、可靠性、代表性的要求。NGSA-II模型中决策变量为12个月末水位,程序参数设置 [11] :种群数pop = 50,循环代数gen = 600,交叉和变异概率分别取0.8和0.2,选择概率取0.9。
4.2. 计算结果与分析
根据上述构建的多目标调度模型,本文采取NSGA-II求解。模型的计算条件包括初始条件和约束条件。
模型初始条件包括来水以及水库调度初始条件。典型年选择:丰水年(25%):1982年7月~1983年6月,平水年(50%):1993年7月~1994年6月,枯水年(75%):1994年7月~1995年6月。水库调度的初始条件为:三河口水库典型年起调水位为585 m [12] ,三河口水电站的出力系数取8.5。
模型的约束条件主要为水库运行的边界条件和决策变量约束,边界条件如下:
1) 非汛期水位约束:三河口水库正常蓄水位643 m;死水位558 m。
2) 汛期水位约束:三河口水库汛限水位642 m;死水位558 m。
3) 水库下泄流量约束:三河口最大下泄流量1560 m3/s,河道最小生态流量2.71 m3/s。
4) 水电站出力约束:三河口电站装机容量60 MW,无保证出力约束。
5) 输水管道限制:最大输水流量70 m3/s。
决策变量约束:以水量平衡约束决策变量变化范围,决策变量不满足时通过反馈修正,直至满足约束。
4.2.1. 水库运行指标分析
多目标模型计算得到的初步结果包括入、出库径流变化过程,出力过程,水位变化过程等,从中提取水位、下泄流量和发电量变化过程作为水库运行的评价指标,分析结果如下:
1) 水位。图3为典型年月末水位变化过程。分析得到:① 典型年最高水位618 m,最低水位585 m,满足水位约束。② 典型年水位呈现丰、平、枯依次从高到低的趋势,符合水库入库径流条件。③ 枯水年水位呈现双峰形状,部分月份高于丰、平水年,主要原因为入库径流的不均匀性。④ 典型年水位变化趋势相同,表现为:水位持续上升至最高,后维持在较高水平,直至汛期前降低水位至起调水位。对应原因为:水库存蓄汛期(7月~10月)富余水量,抬高水位,直至汛前降至汛限水位以下。⑤ 典型年水库均未蓄满,主要原因为起调水位选择过低。
2) 下泄流量。图4为典型年月平均下泄流量过程。分析得到:① 下泄流量满足最小生态流量要求。② 典型年下泄流量呈现丰、平、枯依次从大到小的趋势,符合水库入库径流条件。③ 下泄流量只在丰水年5月份超过输水能力,有利于最大程度用于调水。④ 下泄过程集中在汛期和汛期前;下泄变化过程相似,表现为:下泄流量先增大后减少维持在较低水平,直至汛期前增大。对应原因为:汛期入库径流大,下泄流量大,随后下泄流量减少以抬升水位,直至汛前增加下泄降低水位,其变化过程与图2和图3相对应。
3) 发电量。图5为典型年月发电量过程。分析得到:① 典型年发电量分别为1.68亿kW·h、1.40亿kW·h和0.91亿kW·h;平均发电量为1.32亿kW·h,满足发电量合理性要求。② 发电量主要集中在汛期和汛期前,对应原因为:汛期和汛期前下泄流量大,发电流量大,产生发电大;其它时段发电水头差别不大,发电流量偏小,发电量较小。
4.2.2. 水库调度目标分析
三河口水库调度目标应从水库发电量目标和水库调水量目标两方面进行分析,绘制典型年Pareto曲线如图6所示。
分析调水量目标得到:丰、平、枯水年最大调水量分别为8.75亿m3、7.05亿m3和4.57亿m3,最小调水量为枯水年3.75亿m3;典型年多年平均调水量6.48亿m3。分析发电量目标得到:丰、平、枯水年最大发电量分别为1.65亿kW·h、1.48kW·h和1.34亿kW·h;最小发电量为枯水年0.91亿kW·h。典型年多年平均发电量

Figure 3. Water level change in typical years
图3. 典型年水位变化过程

Figure 4. Discharge flow change in typical years
图4. 典型年下泄流量变化过程

Figure 5. Power generation change in typical years
图5. 典型年发电量变化过程
1.34亿kW·h。图6中Pareto曲线呈现出负线性相关关系,对图形斜率k进行计算得到平水年斜率最大。表明平水年最大调水量和最大发电量之间竞争最大,进一步分析原因为:枯水年没有满足需水的情景,优化空间不大;平水年可以满足需水要求,优化空间较大,但没有丰水年来水丰富,因此表现出平水年竞争最大的特征。此外,发电量相比调水量优化空间不大,为具体分析调水量和发电量的转化关系,分别对平、枯水年建立线性关系计算得到:平水年发电量小幅度减少0.57%,调水量显著增加7.1%;枯水年发电量小幅度减少0.54%,调水量显著增加8.2%。
4.2.3. 影响因素分析
上述分析得到起调水位和入库径流影响水库调度。因此,本文选取起调水位和入库径流作为影响因素,进一步分析其对调度目标的影响。
1) 起调水位。取604和624 m作为不同的起调水位 [12] ,采用平水年数据计算结果如图7(a)和图7(b)所示。
图6平水年和图7对比得到:① 随着起调水位增高,调水量变化愈趋于稳定。② 发电量随起调水位增加显著提高。对应原因为:起调水位越高,发电水头,相同流量条件下水库发电量增加。③ 对上述数据拟合得得到:y = 0.159x + 1.351,即在相同入库径流和水位正常区间范围内,三河口水利枢纽起调水位平均每增加1 m,发电量增加159万kW·h。
2) 入库径流。分析图6得到:① 入库径流对调水量影响显著,丰水年优化空间较小,平水年和枯水年优化空间较大。② 入库径流对发电量影响显著,丰水年发电量优化空间较小,平水年和枯水年发电量优化量较大。3、对图6平水年和枯水年建立线性方程分析得到:平水年三河口水库的调水量每增加1000万m3,对应发电量减少80万kW·h;枯水年三河口水库的调水量每增加1000万m3,对应发电量减少54万kW·h。
4.2.4. 优化结果的合理性和优越性分析
采用NSGA-II优化结果同规划值对比,结果如表1所示。其中,因缺乏工程初期发电规划,本文选取“黄三”

Figure 6. Comparison of dynamic planning and NSGA-II
图6. 动态规划和NSGA-II结果对比
 (a)
(a) (b)
(b)
Figure 7. Pareto curves in different initial operation water levels
图7. 不同起调水位对应的Pareto曲线

Table 1. Comparison of design values and NSGA-II
表1. 优化结果与规划值对比

Table 2. Comparison of dynamic planning and NSGA-II
表2. 动态规划和NSGA-II结果对比
联合调度中三河口电站规划值,结果表明优化结果优于联合调度,则其对单库调度效果更显著。采用动态规划计算单目标调度模型作为参照,以平水年数据计算,结果分别如图6和表2所示。通过对比,验证了优化结果的合理性和优越性。
4.2.5. 调水极值分析
引汉济渭调水工程初期三河口水库运行首要目标就是调水,因此需要分析工程在不同情形下调水极值,判断工程最大和最小调水情景,为进一步研究和制定应对措施做一定基础。分析图6得到三河口水库最大调水量情景为丰水年,最大调水量达到8.75亿m3;最不利调水情景为枯水年,最小调水量只有3.75亿m3。
综上,通过对建立的多目标模型优化求解,揭示了三河口水库的发电与调水目标转化规律,探讨起调水位和入库径流对三河口水库多目标关系的影响。作为参考,实际调度中应适当提高起调水位,即在满足初期调水需求和不威胁水库安全的基础上,将水库起调水位提高到590 m左右;其次,在可预报范围内做好应对枯水年的措施,例如前期多蓄水或多水源联合调度以满足枯水年要求;最后,优化调度结果表明小幅度减少发电量可显著增加调水量,因此实际运行应以调水量最大为调度目标,以达到充分利用水资源和增加工程效益的目的。
5. 结论和展望
本文以三河口水库为研究对象,针对其研究不足的问题,通过建立三河口水库多目标调度模型,采用NSGA-II求解模型,分析调度指标、调度目标以及影响因素等,取得了以下成果:
1) 模型优化结果表明水库发电量和调水量呈多目标关系;同时分析多目标转化规律得到,小幅降低发电量可以显著增加调水量。
2) 分析影响因素得到,入库径流对三河口水库影响显著,三河口水库在丰水年、平水年能够满足规划值,但枯水年不能满足规划值;起调水位对发电量影响显著,量化了起调水位对发电量的影响。
3) 模型优化结果与规划值、动态规划结果对比可知,优化结果提高了水库发电量和调水量,增加了水资源利用效率,验证了优化结果的合理性和优越性。
4) 结合三河口水库实际情况,给出了三河口水库运行的建议和指导意见。下一步将深入开展水库长系列优化调度与多水源联合优化调度研究。
基金项目
国家重点研发计划(2017YFC0405900);陕西省水利科技计划(2017slkj-16, 2017slkj-27);中国博士后科学基金资助项目(2017M623332XB);陕西省自然科学基础研究计划项目(2018JQ5145)。