1. 引言
胶接接头由被粘贴构件和胶粘剂所构成,起着传递载荷的作用。实际工程应用的胶接接头类型有对接接头、斜接接头、搭接接头、套接接头等。搭接接头就是平板被粘物涂胶后叠合在另一平板被粘物端部一定长度上,使之成为一体的接头形式。搭接接头有单搭接、平接、双搭接等形式。搭接接头存在载荷传递不均匀的缺点,即胶层切应力分布不均匀。有关的理论分析模型不止一种。最早的是Volkersen在1938年提出的胶接接头单面搭接模型分析理论 [1] 。1944年Goland和Reissner考虑加载作用线偏心引起的弯曲效应,建立了包括胶层剥离正应力在内的一维梁模型理论 [2] 。1978年Ojalvo假定胶层很薄时,胶层位移沿厚度线性变化, 考虑胶层剪应变完整的几何方程,得到了胶层剪应力沿厚度线性变化的应力表达式 [3] 。但如何测量接头内部胶层的切应力分布,至今没有很好的试验方法进行验证。由于胶层很薄,一般在0.2 mm左右,直接测量胶层的切应力难度很大。L. Goglio等只对局部进行了应变测量,没有对接头整体进行测试,并且试验中只测试了搭接盖板正应力,没有测试胶层的切应力 [4] 。M.-P. Moutrille,等人用光学的方式对铝板和复合物之间的胶结区的切应力和位移场进行了测量,但是测试结果离散程度较大 [5] 。
本文提出了一种测量双面搭接接头胶层切应力的测试方法。通过测量盖板正应力,利用胶层位置盖板正应力与胶层切应力的对应关系,间接求出胶层切应力。在双面搭接接头试样的搭接盖板上粘贴多个应变计,对接头施加拉力。根据盖板材料的应力–应变关系,计算出盖板各测点的正应力,应用最小二乘法将各测点正应力按照双曲函数形式拟合,得到正应力分布函数,再根据接头内部的平衡微分方程求出胶层切应力分布函数,进而求得任意位置的胶层切应力。
2. 测试方法
2.1. 测试原理
胶接接头通常采用单面搭接形式,如果不考虑荷载偏心的影响,可以简化为两块搭接盖板用胶连接而形成,两端作用一个大小相等方向相反的力的受力模型,如图1所示。
这一理论模型首先由Volkersen提出的,假设胶接接头盖板只发生纵向的形变,而且胶层的切应力是连续的。根据搭接盖板的平衡微分方程和边界条件 [1] 联立求解得:
(1)
(2)
式中:
为厚度为t1盖板中正应力,t为胶层切应力:
根据上述理论分析的结果,盖板上的正应力与胶层中的切应力存在平衡微分关系如下式。
(3)
式中:σ(x)——盖板上的正应力分布函数;
t1——盖板的厚度;
τ(x)——胶层中的切应力分布函数。
从公式(3)的关系中不难发现,如果能测出盖板上的正应力分布函数,就可以通过公式(3)推出胶层中的切应力分布函数,从而计算出胶层中的切应力。如果在模型盖板的胶结区域多个测点上粘贴应变计,对试样施加拉力,测出各测点的应变,再根据盖板材料的应力–应变关系,测出各点的正应力,用最小二乘法将测点正应力按照双曲函数形式进行曲线拟合,得到正应力分布函数,那么便可以根据公式(3)求出胶层切应力分布函数,进而求得胶层各点的切应力。
2.2. 测试方案
接头模型的一半,因此测试可以采用双面搭接接头试样,如图2所示。接头盖板采用铝合金材料,胶层材料为合众高性能结构AB胶。
试样尺寸和材料参数如表1所示。
2.3. 测试过程
首先制作试样,按照表1的尺寸制作两个接头试样(试样一、试样二)。其次确定测点位置,粘贴应变
计。测点位置见图3。电阻应变计选用BX120-2AA,敏感栅尺寸为1 × 2 mm,电阻阻值为120 Ω,灵敏系数为2.08。应变计在上下盖板呈等间距对称布置,如图3所示。
采用Instron 3367电子万能试验机加载,按单向拉伸加载。应变测试采用4501 A应变仪。预加载1 kN,最大荷载为6 kN,分级加载,每隔1 kN记录一次数据,重复3次。试验加载见图4。
3. 测试结果
3.1. 盖板正应力测试结果
按测试方案要求,分别在1、2、3、4、5、6 kN读取相应的应变值。取各测点的应变增量的平均值,根据盖板材料应力-应变关系计算各测点的正应力。测试结果如表2和表3所示,表3中的正应力理论值依据式(1)与表1中的参数计算得到:
对盖板正应力实测数据与理论数据进行比较,如图5所示。两者在中点处基本吻合,误差很小,不到1%;两个端点的数据也较为接近。

Figure 3. Position of the strain gage
图3. 贴片位置及坐标示意图

Table 2. The strain of the test position
表2. 测点应变

Table 3. Normal stress of the test position and its theoretical result
表3. 测点正应力试验值与理论值对比
3.2. 胶层切应力测试结果
根据公式(1)可知,参数
为接头材料固有属性,与作用的荷载无关,故不参与拟合计算。而公式(1)中的参数A、B、C均与荷载有关,因此用可各测点实测结果拟合出正应力分布函数,也是荷载作用的客观反映。
将表3中各测点的正应力按照公式(1)所示双曲函数形式利用MATLAB软件进行最小二乘法拟合,得到参数A、B、C,如表4所示。
再根据接头微段平衡方程,通过拟合的正应力分布函数求得胶层切应力分布函数:
(4)
公式(4)中的A、B就是表4中拟合结果,代入公式(4)不难求出各测点的切应力,如表5所示。
通过表5的数据可知,两个试样的测试结果与理论分析结果的趋势完全一致。试样1在两端数据的最大相对误差为9.6%,试样2在两端数据的最大相对误差为26.3%。胶层切应力实测数据与理论结果对比见图6。从图中看实测结果与理论分析趋势完全一致,切应力分布是不均匀的,在两个端点切应力最
大,存在切应力集中现象。若将两端切应力最大值
与假设胶层切应力均匀分布的结果
相比较,定义两端应力集中系数:
(5)
则左端集中系数
可达1.8,右端集中系数
可达3.2。

Table 4. The fitting result of normal stress distribution coefficients
表4. 测点正应力分布参数拟合结果

Table 5. Test of the shear stress distribution and its theoretical result
表5. 胶层切应力实测值与理论值的比较
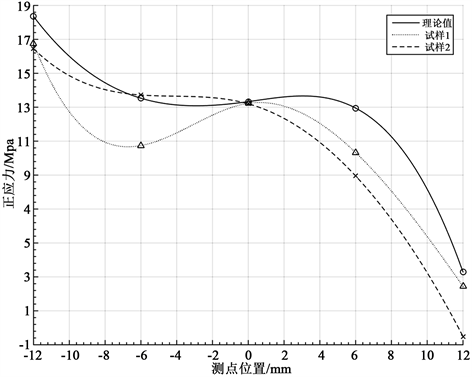
Figure 5. Normal stress of the test position and its theoretical result
图5. 正应力理论值与试验值对比
4. 结论
两个试样的试验数据基本一致,离散性不大,试验结果较为可靠。接头盖板正应力的测试结果与理论计算结果接近,在中间点处与理论值相差最小,相对误差不到1%,故测试结果较有可信度,而且与推算得到的胶层切应力分布与理论分析吻合,在胶层两端的切应力最大,说明胶层中的切应力分布是不均匀的,表现出切应力两端大中间小的应力集中现象,说明该试验方法是有效的。
测试区域两端有一定的误差,可能是由于应力集中现象造成的,还有可能是端部效应影响造成,这

Figure 6. Shear stress of the test position and its theoretical result
图6. 切应力理论值与试验值对比
在后续的研究需要进一步完善。另外结果的偏差还有可能来自于胶层的不均匀性与缺陷的影响,这些因素在后续的试验研究中应予以考虑。