1. 引言
随着材料学、电磁学、电力电子器件和现代控制技术的发展,无线电能传输(wireless power transfer, WPT)已经步入人们的生活。传统电能是通过插孔、导线、插头等接触器的连接进行传输,由于导线的磨损、损坏、老化、外漏与摩擦,很容易产生电击、电火花现象,不仅导致供电可靠性、安全性下降,而且大大降低电气设备的使用寿命。在油田开采、矿井等特殊领域,不良的导线连接会增大接触电阻,导致线路温度升高,导线因摩擦极易产生电火花,从而引起爆炸,造成严重的损失 [1] 。
无线电能传输没有导线相互连接,即用电设备以非接触方式从固定电网获取电能,是一种安全、可靠的能量传输形式 [2] 。无线电能传输不仅能避免导线插拔、断路等弊处;还能在保证电能稳定可靠的基础上,解决房屋导线杂乱、插孔破坏装饰等问题,使得人们生活更加美观便利高效。因此无线电能传输技术被列为“10大引领未来的科学技术”之一。无线电能传输是实现能源方便便捷、高效利用的重要途径,在电动汽车充电 [3] 、航空航天器供能、便携式移动设备充电、医疗器械设备供电和煤矿油田开采、能源化工、水下作业等特殊领域具有广阔的应用前景,对磁耦合理论的发展和充电技术具有重要的应用和研究价值 [4] 。
2007年美国麻省理工学院(MIT)的Marin Soljacic教授课题组提出了磁耦合谐振式无线电能传输理论,并在传输距离为2 m时点亮60 W的灯泡 [5] 。磁耦合谐振式无线电能传输具有传输效率高、传输距离远、传输功率大以及对介质依赖性小等优点 [6] ,为无线电能中等传输距离的研究指明了方向,因此磁耦合谐振式无线电能传输技术的研究立即受到世界各国科研学者的关注。
该项技术的深入研究分析可以为其扩大在多个领域内的实际应用范围提供理论基础的支持。随着该技术越来越深入的研究,其实用价值日益增加,人们已将该技术应用到了各种便携式的移动设备装置中。相信在不久以后,无线电能传输技术必将广泛应用到工业、民用和医疗等各类场所,且具有极大的市场应用价值。
2. 系统模型和理论分析
2.1. 系统模型
本文所研究的磁耦合谐振式无线电能传输的系统结构简化电路模型如图1所示。系统由两个具有相同谐振频率的LC串联谐振回路组成,考虑到逆变电路的开关损耗,电源具有内阻R0;由于具有相同的谐振频率,设发射线圈和接收线圈具有相同的电容、电感和电阻,即CS = CD,LS = LD,RS = RD;设接收线圈所接负载为RL。
2.2. 理论分析
本节利用电路理论对所研究的磁耦合谐振式无线电能传输系统的功率传输特性和效率特性进行分析,分析线圈半径对磁耦合谐振式无线电能传输的影响 [7] 。
2.2.1. 系统功率传输特性
利用KVL定律,得到发射线圈和接收线圈中的电流分别为
(1)
式中,
,
,
且:
,
,
,
,
M为发射和接收线圈之间的互感。
(2)
对于同轴平行放置的两线圈,线圈半径分别为r1和r2,匝数分别为n1和n2,轴向距离为D,它们之间的互感为

Figure 1. Magnetic coupling resonant radio transmission system simplified model
图1. 磁耦合谐振无线电能传输系统简化模型
(3)
式中,
。
由该式可知,对于两同轴放置的线圈,互感M与两线圈之间的轴向距离D、线圈匝数n1、n2以及线圈半径r1、r2有关。
对于具有对称结构,即电路参数相同的发射和接受线圈,系统满足
,
,即可将互感M的表达式简化为
(4)
由图1所示的等效电路模型可知,当RL = RS,即满足阻抗匹配时,该二端口网络实现最大功率传输。所研究的两种线圈半径情况下,输出功率PLoad关于电源角频率ω和谐振线圈轴向距离D的关系曲面分别如图2(a)和图2(b)所示。
由图2可以看出,磁耦合谐振式无线电能传输系统的输出功率在强耦合区,即临界耦合距离内发生频率分裂现象。且在强耦合区内任一传输距离处,系统均在分裂谐振频率处达到最大传输功率,且当系统阻抗匹配,即RS = RL时,所能达到的最大输出功率保持不变。由于线圈电阻存在少许差异,系统所能达到的最大输出功率分别为59 W和56 W [8] 。系统在临界耦合距离处满足条件
(5)
结合式(4)可以得到临界耦合距离D0由线圈半径r,线圈匝数n,线圈导线截面圆半径a和电源频率f共同决定。
2.2.2. 系统效率特性
系统效率为
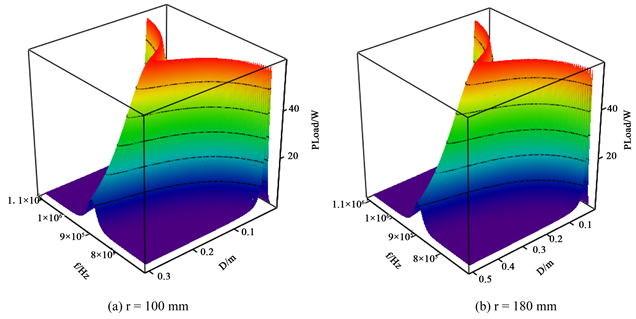
Figure 2. Relational surface diagram of PLoad, ω, D
图2. PLoad、ω、D关系曲面图
(6)
式中,
由式(6)可以看出η是关于X和D的表达式,其所对应两种线圈半径情况下的曲面图如图3所示。
由图3可以看出,磁耦合谐振式系统效率在固有谐振频率处达到最大值。考虑到两线圈电阻的差异,系统所能达到的最大效率分别达93%和90%。
3. 线圈半径对磁耦合谐振式无线电能传输特性的影响
本文对100 mm和180 mm两种线圈半径情况下的磁耦合谐振式无线电能传输特性进行分析,通过改变其匝数以保持它们的感量相当。利用有限元软件计算得它们在相同电感情况下的线圈匝数分别为9匝和6匝。分析线圈半径对输出功率的频率特性和系统效率的距离特性的影响 [9] 。
3.1. 线圈半径r对传输系统两线圈间互感M的影响
利用有限元软件计算得到两同轴平行线圈间的互感随距离的变化曲线大致如图4所示。
由图4可以看出:
1) 线圈半径r对两线圈间的互感影响很大。在距离不变的情况下,线圈间的互感随线圈半径的增大而增大;
2) 随着距离的增大,线圈间的互感均单调减小。从而得到线圈半径r和传输距离D是影响系统互感的主要因素,这亦可从式(4)中看出。
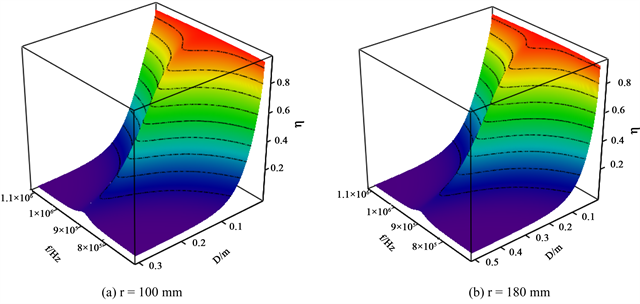
Figure 3. Relational surface diagram of PLoad, ω, D
图3. PLoad、ω、D关系曲面图
 (a) r = 100 mm
(a) r = 100 mm  (b) r = 180 mm
(b) r = 180 mm
Figure 4. The relationship of mutual inductance and distance between two coils
图4. 两线圈间互感随距离的关系
3.2. 线圈半径r对系统输出功率的频率特性的影响
由式(2)可得,当电源频率固定为线圈自然谐振频率时,归一化的输出功率随距离的变化规律如图5所示。此外,还可由式(2)得出,在不同传输距离时,所研究两种线圈半径情况下的谐振线圈所对应的归一化输出功率随频率的变化曲线如图6所示。
由图5可知,对于所研究的磁耦合谐振系统,系统分别在0.16 m和0.255 m处达到临界耦合状态。结合式(5)可知,在发射和接收线圈参数已经确定的情况下,系统的有效传输距离主要由线圈半径r决定。对照图4可知,当电源频率为905 kHz时,100 mm和180 mm两种线圈半径情况下系统的临界耦合距离所对应的互感均在1.8~1.9 μH左右,与式(5)所得结果一致。结合式(4),当谐振系统已经确定,即线圈匝数n和临界耦合状态时的互感M一定的情况下,随着线圈半径r的增大,为了维持等式两边相等,最大功率的有效传输距离也将不断增大,即谐振系统的有效传输距离随线圈半径的增大而增大。
由图6(a)和图6(b)可知:1、当谐振系统处于强耦合区,即传输距离小于临界耦合距离时,系统将发生频率分裂现象;2、系统的分裂频率均在临界耦合点汇合,此时的系统谐振频率为线圈自然谐振频率,且输出功率最大不变;3、当系统处于弱耦合区时,系统不发生频率分裂现象,系统输出功率在自然谐振频率处达到最大值,且随传输距离的最大而急剧下降;4、谐振系统的临界耦合距离,即有效传输距离随线圈半径的增大而增大。
由图7可知,半径分别为100 mm和180 mm的线圈分别相距140 mm和250 mm时的发射和接收线圈周围所感应磁场分布利用有限元软件计算得到100 mm和180 mm两种线圈半径情况下,系统处于临界耦合状态时,发射线圈和接收线圈周围所感应磁场的分布情况分别如图7(s)和(b)所示。从而得到理论分析结果与有限元计算结果的一致性。
3.3. 线圈半径r对系统效率的距离特性的影响
固定电源频率为线圈自然谐振频率,改变系统传输距离D,得到不同线圈半径情况下,系统效率的理论计算结果和有限元仿真结果随传输距离的变化曲线如图8所示。
由图8可以看出:
1) 理论计算结果与有限元瞬态仿真结果具有完全一致性,从而验证了理论分析的正确性;
2) 随着传输距离的最大,系统效率均单z减小,且在同等传输距离的情况下,线圈半径较大的传输系统具有较大的效率;
3) 在同等传输效率情况下,线圈半径较大的传输具有更远传输距离的能力。

Figure 5. The normalized output power varies with the distance
图5. 归一化的输出功率随距离的变化规律
 (a) r = 100 mm
(a) r = 100 mm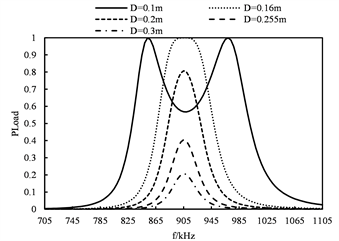 (b) r = 180 mm
(b) r = 180 mm
Figure 6. The normalized output power varies with the distance
图6. 归一化的输出功率随距离的变化规律
 (a) 线圈半径100 mm,距离为160 mm
(a) 线圈半径100 mm,距离为160 mm  (b) 线圈半径180 mm,距离为255 mm
(b) 线圈半径180 mm,距离为255 mm
Figure 7. Induced field distribution
图7. 感应磁场分布
4. 实验分析
基于本文的研究方向,即在谐振线圈电感不变的情况下,线圈半径不同的谐振线圈对有效传输距离的影响,搭建了如图9所示的实验装置。
得到了如图10所示的实验波形。
5. 结论
由图10可知:线圈半径分别在5 cm、10 cm、15 cm、20 cm四种情况下,负载上接收到的电压在20 cm、
 (a) r = 100 mm
(a) r = 100 mm  (b) r = 180 mm
(b) r = 180 mm
Figure 8. The system efficiency varies with the transmission distance
图8. 系统效率随传输距离的变化曲线
45 cm、60 cm、75 cm的距离处开始显著下降;在20 cm、45 cm、60 cm、75 cm的距离处负载上接收到的电压分别为最大值的 85%、85%、90%、85%。图中存在一定的误差主要是线圈手工绕制和忽略辐射损耗造成的,因此可以证明有效传输距离与线圈半径成正比。