关于特殊矩阵求特征值的新方法

doi:10.12677/AAM.2018.74037

期刊菜单

关于特殊矩阵求特征值的新方法
A New Method to Find Eigenvalues of Special Matrices

DOI: 10.12677/AAM.2018.74037, PDF, HTML, XML, 下载: 1,814 浏览: 3,053
作者: 谭尊林, 赵春娥, 程志远：中国石油大学(华东)，理学院，山东青岛
关键词: 分块矩阵；行列式计算；特殊矩阵；Partitioned Matrix； Determinant Calculation； Special Matrix

摘要: 求矩阵的特征值在众多领域中有重要的作用，但实际操作起来比较繁琐。本文利用行列式计算的相关性质并结合分块矩阵的乘法，提供两种计算特殊矩阵求特征值的通用简便方法。简化计算步骤，提高计算效率。

Abstract: The eigenvalues of the matrix have an important role in many fields, but they are very complicated in practice. In this paper, we use the correlation property of determinant calculation and the multiplication of partitioned matrix to provide two general and simple methods for calculating eigenvalues of special matrices, simplifying calculation steps to improve computational efficiency.

文章引用：谭尊林, 赵春娥, 程志远. 关于特殊矩阵求特征值的新方法[J]. 应用数学进展, 2018, 7(4): 310-315. https://doi.org/10.12677/AAM.2018.74037

1. 引言

在线性代数领域中，矩阵的特征值在高等代数中占据着较为重要的地位。求矩阵A的一般方法为：通过一系列行列式的初等变换将 $| A - λ E |$ 化为特征多项式，然后求得特征值。对于此方法，计算量大，易于出错。本文给出的两种计算特殊矩阵的特征值的方法：其一，利用分块矩阵及行列式的计算性质，将2n阶的方阵降阶为n阶；其二，利用矩阵的乘法，将n阶方阵降阶为向量的乘积。两种方法均简化计算，减轻了计算的工作量。

2. 特殊矩阵的分块求特征值

定理1：设 $A_{2 n} = [\begin{matrix} A & B \\ C & D \end{matrix}]$ ，其中 $A_{2 n}$ 为2n阶方阵，A、B、C、D均为n阶方阵，若A可逆，且 $A C = C A$ ，

则：

$| A_{2 n} - λ E | = | (A - λ E) (D - λ E) - C B |$

证明：∵A，B，C，D均为方阵，且A可逆， $A C = C A$ [1] 。

∴ $| \begin{matrix} A & B \\ C & D \end{matrix} | = | A D - C B |$

∴ $| A_{2 n} - λ E | = | \begin{matrix} A - λ E & B \\ C & D - λ E \end{matrix} |$

∵ $(A - λ E) C = A C - λ E C = A C - λ C = C A - C λ E$

∴ $(A - λ E) C = C (A - λ E)$ 且矩阵 $A - λ E$ 可逆；

∴ $| A_{2 n} - λ E | = | (A - λ E) (D - λ E) - C B |$

例1. 已知 $A_{4} = (\begin{matrix} 1 & - 1 & - 1 & 1 \\ - 1 & 1 & 1 & - 1 \\ - 1 & 1 & 1 & - 1 \\ 1 & - 1 & - 1 & 1 \end{matrix})$ ，求该矩阵的特征值。

解：1) 对于一般求解法：

$\begin{matrix} | A_{4} - λ E | = | \begin{matrix} 1 - λ & - 1 & - 1 & 1 \\ - 1 & 1 - λ & 1 & - 1 \\ - 1 & 1 & 1 - λ & - 1 \\ 1 & - 1 & - 1 & 1 - λ \end{matrix} | = | \begin{matrix} 1 - λ & - 1 & - 1 & 1 \\ - 1 & 1 - λ & 1 & - 1 \\ 0 & λ & - λ & 0 \\ 0 & 0 & - λ & - λ \end{matrix} | \\ = (1 - λ) | \begin{matrix} 1 - λ & 1 & - 1 \\ λ & - λ & 0 \\ 0 & - λ & - λ \end{matrix} | + | \begin{matrix} - 1 & - 1 & 1 \\ λ & - λ & 0 \\ 0 & - λ & - λ \end{matrix} | \\ = (1 - λ) [(1 - λ) | \begin{matrix} - λ & 0 \\ - λ & - λ \end{matrix} | - λ | \begin{matrix} 1 & - 1 \\ - λ & - λ \end{matrix} |] + | \begin{matrix} - 1 & - 1 & 1 \\ 0 & - 2 λ & λ \\ 0 & - λ & - λ \end{matrix} | \\ = λ^{3} (λ - 4) \end{matrix}$

求得矩阵 $A_{4}$ 的特征值为： $λ_{1} = 0$ (三重根)， $λ_{2} = 4$ 。

2) 对于简便求解法：

将矩阵 $A_{4}$ 分块为： $A_{4} = (\begin{matrix} A & B \\ C & D \end{matrix})$ ；
其中 $A = (\begin{matrix} 1 & - 1 \\ - 1 & 1 \end{matrix})$ ，， $C = (\begin{matrix} - 1 & 1 \\ 1 & - 1 \end{matrix})$ ， $D = (\begin{matrix} 1 & - 1 \\ - 1 & 1 \end{matrix}) = A$ 。

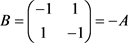显然：矩阵A可逆；

又因为 $A C = - A A = C A$

故由定理1得： $\begin{matrix} | A_{4} - λ E | = | {(A - λ E)}^{2} - A^{2} | = | (A - λ E - A) (A - λ E + A) | \\ = | \begin{matrix} λ (λ - 2) & 2 λ \\ 2 λ & λ (λ - 2) \end{matrix} | = λ^{3} (λ - 4) \end{matrix}$

求得矩阵 $A_{4}$ 的特征值为： $λ_{1} = 0$ (三重根)， $λ_{2} = 4$ 。

推论1: 设 $A_{2 n} = [\begin{matrix} A & B \\ C & D \end{matrix}]$ ，其中 $A_{2 n}$ 为2n阶方阵，A、B、C、D均为n阶方阵，若D可逆，且 $C D = D C$ ，

则： $| A_{2 n} - λ E | = | (A - λ E) (D - λ E) - B C |$

证明：∵A，B，C，D均为方阵，且D可逆， $C D = D C$ ；

∵ $| \begin{matrix} A & B \\ C & D \end{matrix} | = | A - B D^{- 1} C | | D | = | A D - B D^{- 1} C D | = | A D - B C |$

∴ $| A_{2 n} - λ E | = | (A - λ E) (D - λ E) - B C |$

例2. 已知 $A_{4} = (\begin{matrix} 2 & 0 & 0.5 & 0 \\ 1 & 1 & - 0.5 & 1 \\ 0.5 & 0 & 2 & 0 \\ - 0.5 & 1 & 1 & 1 \end{matrix})$ ，求该矩阵的特征值。

解：用推论1可将矩阵 $A_{4}$ 分块为 $(\begin{matrix} A & B \\ C & D \end{matrix})$ ，其中 $A = (\begin{matrix} 2 & 0 \\ 1 & 1 \end{matrix})$ ， $B = (\begin{matrix} 0.5 & 0 \\ - 0.5 & 1 \end{matrix})$ ， $C = (\begin{matrix} 0.5 & 0 \\ - 0.5 & 1 \end{matrix})$ ， $D = (\begin{matrix} 2 & 0 \\ 1 & 1 \end{matrix})$ 。

因为矩阵D可逆，且满足 $C D = D C$ 。

所以

$\begin{matrix} | A_{4} - λ E | = | A_{2 n} - λ E | = | (A - λ E) (D - λ E) - B C | \\ = | [\begin{matrix} {(2 - λ)}^{2} & 0 \\ 3 - 2 λ & {(2 - λ)}^{2} \end{matrix}] + [\begin{matrix} 1 & - 0.75 \\ 0 & 0.25 \end{matrix}] | \\ = \frac{1}{4} λ (2 λ - 3) (2 λ - 5) (λ - 2) \end{matrix}$

解得特征值分别为： $λ_{1} = 0$ ， $λ_{2} = 1.5$ ， $λ_{3} = 2.5$ ， $λ_{4} = 2$ 。

3. 特殊矩阵的分解求特征值

定理2：已知n阶方阵 $M_{n} = A^{T} A$ ，其中 $A = (a_{1} a_{2} a_{3} \dots a_{n})$ ，其中 $a_{i} (i = 1, 2, \dots, n)$ 不全为0。则 $M_{n}$ 的特征值为： $λ_{1} = 0$ ( $n - 1$ 重根)， $λ_{2} = A A^{T}$

$M_{n}$ 的特征向量为：

当 $λ = 0$ 时：

$η_{1} = (\begin{matrix} a_{2} \\ \begin{matrix} - a_{1} \\ 0 \\ ⋮ \\ 0 \end{matrix} \end{matrix})$ ， $η_{2} = (\begin{matrix} a_{3} \\ \begin{matrix} 0 \\ - a_{1} \\ ⋮ \\ 0 \end{matrix} \end{matrix})$ ， $η_{n - 1} = (\begin{matrix} a_{n} \\ \begin{matrix} 0 \\ 0 \\ ⋮ \\ - a_{1} \end{matrix} \end{matrix})$

当 $λ = a_{1}^{2} + a_{2}^{2} + \dots + a_{n - 1}^{2} + a_{n}^{2}$ 时：

$η_{n} = (\begin{matrix} a_{1} \\ \begin{matrix} a_{2} \\ a_{3} \\ ⋮ \\ a_{n} \end{matrix} \end{matrix})$

证明：1) 对于一般解法：

$\begin{matrix} A_{n} = | λ E - A^{T} A | = | \begin{matrix} λ - a_{1}^{2} & - a_{1} a_{2} & \dots & - a_{1} a_{n} \\ - a_{2} a_{1} & λ - a_{2}^{2} & \dots & - a_{2} a_{n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ - a_{n} a_{1} & - a_{n} a_{2} & \dots & λ - a_{n}^{2} \end{matrix} | \\ = | \begin{matrix} λ & 0 & \dots & 0 \\ - a_{2} a_{1} & λ - a_{2}^{2} & \dots & - a_{2} a_{n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ - a_{n} a_{1} & - a_{n} a_{2} & \dots & λ - a_{n}^{2} \end{matrix} | + | \begin{matrix} - a_{1}^{2} & - a_{1} a_{2} & \dots & - a_{1} a_{n} \\ - a_{2} a_{1} & λ - a_{2}^{2} & \dots & - a_{2} a_{n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ - a_{n} a_{1} & - a_{n} a_{2} & \dots & λ - a_{n}^{2} \end{matrix} | \\ = λ | \begin{matrix} λ - a_{2}^{2} & 0 & \dots & 0 \\ - a_{3} a_{2} & λ - a_{3}^{2} & \dots & - a_{3} a_{n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ - a_{n} a_{2} & - a_{n} a_{3} & \dots & λ - a_{n}^{2} \end{matrix} | + a_{1} | \begin{matrix} a_{1} & a_{2} & \dots & a_{n} \\ 0 & λ & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & \dots & λ \end{matrix} | \\ = λ A_{n - 1} - a_{1}^{2} λ^{n - 1} \end{matrix}$

由于递推公式：

${\begin{cases} A_{n} = λ A_{n - 1} - a_{1}^{2} λ^{n - 1} \\ A_{n - 1} = λ A_{n - 2} - a_{2}^{2} λ^{n - 2} \\ ⋮ \\ A_{2} = λ A_{1} - a_{n - 1}^{2} λ \end{cases}$

可得：

$A_{n} = λ^{n - 1} A_{1} - (a_{1}^{2} + a_{2}^{2} + \dots + a_{n - 1}^{2}) λ^{n - 1} = λ^{n} - (a_{1}^{2} + a_{2}^{2} + \dots + a_{n - 1}^{2} + a_{n}^{2}) λ^{n - 1}$

显然， $A_{n} = 0$ ，即可求的特征值：

$λ_{1} = 0$ ( $n - 1$ 重)， $λ_{2} = a_{1}^{2} + a_{2}^{2} + \dots + a_{n - 1}^{2} + a_{n}^{2}$

根据特征值可求的特征向量分别为：

当 $λ = 0$ 时：

$ξ_{1} = (\begin{matrix} a_{2} \\ \begin{matrix} - a_{1} \\ 0 \\ ⋮ \\ 0 \end{matrix} \end{matrix})$ , $ξ_{2} = (\begin{matrix} a_{3} \\ \begin{matrix} 0 \\ - a_{1} \\ ⋮ \\ 0 \end{matrix} \end{matrix})$ , $ξ_{n - 1} = (\begin{matrix} a_{n} \\ \begin{matrix} 0 \\ 0 \\ ⋮ \\ - a_{1} \end{matrix} \end{matrix})$

当 $λ = a_{1}^{2} + a_{2}^{2} + \dots + a_{n - 1}^{2} + a_{n}^{2}$ 时：

$ξ_{n} = (\begin{matrix} a_{1} \\ \begin{matrix} a_{2} \\ a_{3} \\ ⋮ \\ a_{n} \end{matrix} \end{matrix})$

2) 对于简便解答方法：

运用特征值、特征向量的定义可求：

设λ是 $A^{T} A$ 的特征值，ξ是属于λ的特征向量，则： $A^{T} A ξ = λ ξ$

若取 $ξ = (\begin{matrix} a_{1} \\ \begin{matrix} a_{2} \\ a_{3} \\ ⋮ \\ a_{n} \end{matrix} \end{matrix})$

则有 $(\begin{matrix} a_{1} \\ \begin{matrix} a_{2} \\ a_{3} \\ ⋮ \\ a_{n} \end{matrix} \end{matrix}) (a_{1} a_{2} a_{3} \dots a_{n}) (\begin{matrix} a_{1} \\ \begin{matrix} a_{2} \\ a_{3} \\ ⋮ \\ a_{n} \end{matrix} \end{matrix}) = λ (\begin{matrix} a_{1} \\ \begin{matrix} a_{2} \\ a_{3} \\ ⋮ \\ a_{n} \end{matrix} \end{matrix})$

1) 若 $(a_{1} a_{2} a_{3} \dots a_{n}) (\begin{matrix} a_{1} \\ \begin{matrix} a_{2} \\ a_{3} \\ ⋮ \\ a_{n} \end{matrix} \end{matrix}) = 0$ ，则 $λ = 0$ ， $ξ_{1} = (\begin{matrix} a_{2} \\ \begin{matrix} - a_{1} \\ 0 \\ ⋮ \\ 0 \end{matrix} \end{matrix})$ ， $ξ_{2} = (\begin{matrix} a_{3} \\ \begin{matrix} 0 \\ - a_{1} \\ ⋮ \\ 0 \end{matrix} \end{matrix})$ ， $ξ_{n - 1} = (\begin{matrix} a_{n} \\ \begin{matrix} 0 \\ 0 \\ ⋮ \\ - a_{1} \end{matrix} \end{matrix})$ 。

2) 若 $(a_{1} a_{2} a_{3} \dots a_{n}) (\begin{matrix} a_{1} \\ \begin{matrix} a_{2} \\ a_{3} \\ ⋮ \\ a_{n} \end{matrix} \end{matrix}) \neq 0$ ，则 $λ = a_{1}^{2} + a_{2}^{2} + \dots + a_{n - 1}^{2} + a_{n}^{2}$ ，

$ξ_{n} = (\begin{matrix} a_{1} \\ \begin{matrix} a_{2} \\ a_{3} \\ ⋮ \\ a_{n} \end{matrix} \end{matrix})$

例3. 已知 $A = (\begin{matrix} 1 & 3 & 5 & 7 \\ 3 & 9 & 15 & 21 \\ 5 & 15 & 25 & 35 \\ 7 & 21 & 35 & 49 \end{matrix})$ ，求此矩阵的特征值与特征向量。

解：矩阵A可分解为： $A = (\begin{matrix} 1 \\ 3 \\ 5 \\ 7 \end{matrix}) (1 3 5 7)$

当特征值 $λ_{1} = 0$ ：

$ξ_{1} = (\begin{matrix} 3 \\ - 1 \\ 0 \\ 0 \end{matrix})$ ， $ξ_{2} = (\begin{matrix} 5 \\ 0 \\ - 1 \\ 0 \end{matrix})$ ， $ξ_{3} = (\begin{matrix} 7 \\ 0 \\ 0 \\ - 1 \end{matrix})$

当特征值 $λ_{1} = 84$ ：

$ξ_{4} = (\begin{matrix} 1 \\ 3 \\ 5 \\ 7 \end{matrix})$

4. 结论

对于定理1和定理2以及推论1，均可以发现一般的求解方法在计算上较复杂，计算过程中也较容易出错，不方便检查正确与否；文中所给出的简便方法不仅简化了计算，而且便于检查。

致谢

感谢老师给予的无私的指导与鼓励。

参考文献

参考文献

[1]	陈志杰. 高等代数与解析几何(上) [M]. 北京: 高等教育出版社, 2008: 330-340.

为你推荐

友情链接