1. 引言
半金属材料因具有100%的自旋极化率被认为是理想的半导体自旋电子注入源之一。在半金属材料的两个自旋能带中,一个自旋方向的能带呈现金属性,而另一个自旋方向的能带在费米能级处存在能隙,从而导致在费米面附近传导电子的自旋极化率为100% [1] 。
在过去的理论与实验研究中,很多全Heusler合金被预测出具有半金属特性,如Co2基、Mn2基、Ti2基的三元全Heusler合金Co2MnZ (Z = Si, Ge, Sn) [2] ,Mn2CoZ (Z = Al, Si, Ge, Sn, Sb) [3] 、Ti2YZ (Y = Fe, Co, Ni和Z = Al, Ga, In) [4] 等等。最近的第一性原理研究表明,大量的四元全Heusler合金XX’YZ也具有半金属特性,其中X、X’、Y原子为过渡金属元素,Z原子为III到V族元素。四元全Heusler合金XX’YZ按照原子的不同排列方式可形成如图1所示的三种结构。在结构I中X、X’、Y、Z原子分别占据(0, 0, 0)、(1/2, 1/2, 1/2)、(3/4, 3/4, 3/4)、(1/4, 1/4, 1/4)等Wyckoff坐标位置。在结构I中调换X’和Y原子的位置,则形成结构II;当调换X’和Z原子的位置,则形成的是结构III。Gao等人从第一性原理计算预测了四元全Heusler合金CoFeCrZ (Z = Al, Si, Ga, Ge)具有半金属特性,并它们的总磁矩(Mtot)满足Slater-Pauling规律,即Mtot = Ztot − 24,其中Ztot为原胞中总的价电子数目 [5] 。Xu等人利用平面波方法预测到CoFeMnSi,CoFeCrAl,CoMnCrSi,CoFeVSi和FeMnCrSb等四元全Heusler合金具有半金属特性 [6] 。
目前,对四元全Heusler合金的相关文献报道较少。本论文系统研究了四元全Heusler合金FeMnCrAl的晶体结构、电子结构、磁性及半金属特性,为探索适用于自旋电子学器件的半金属材料提供一定的理论基础。
2. 计算方法
Kohn-Sham方程的求解是基于密度泛函理论的全势线性缀加平面波(FLAPW)方法 [7] (采用FLEUR程序包 [8] )以自洽循环来完成。因为四元full-Heusler合金是由多种不同电子结构的元素组合而成,即有局域的d电子轨道又有非局域的s、p电子轨道,所以引入粒子数密度梯度修正的广义梯度近似 [9] 与局域密度近似相比更适合处理具有非均匀密度的电子体系。计算中采用了广义梯度近似。我们把Fe,Mn,Cr
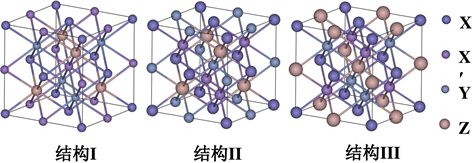
Figure 1. Crystal structure of quaternary full-Heusler XX´YZ alloy
图1. 四元全Heusler XX´YZ合金的晶胞结构图
原子的3d4s态电子取为价电子,而对于Al原子3s3p态电子取为价电子。对Fe,Mn,Cr原子的Muffin-tin半径(RMT)取为1.164 Å,而Al的RMT取为1.217 Å,RMT × Kmax取为8.8,平面波展开过程中的能量截断值取为14 Ry。采用Monkost-Pack方案将布里渊区中的k点进行21 × 21× 21的分割。当输入与输出电荷(自旋)密度之差小于1.0 × 10−5 electrons/(a.u.)3时为收敛标准。
3. 结果与讨论
3.1. 晶体结构
图2是三种结构下四元全Heusler合金FeMnCrAl的总能量随晶格常数的变化关系。三种结构的最优化晶格常数分别为5.662,5.821,5.821 Å。在三种结构中,结构I的能量最低,是四元全Heusler合金FeMnCrAl的基态;结构I的最优化晶格常数与文献 [10] 的值5.67 Å一致。结构II的能量次之,是亚稳态;结构III具有最高的能量。此结果与其它四元全Heusler合金的文献报道相一致 [5] [6] 。
为了了解四元全Heusler合金FeMnCrAl形成的难易程度和结构的稳定性,我们采用公式(1) [11] 和(2) [11] 计算了合金的形成能(ΔH)与结合能(ΔE),并在表1给出了相关结果。
(1)
(2)
其中,EFeMnCrAl、EFe、EMn、ECr、EAl分别表示FeMnCrAl、Fe、Mn、Cr、Al在各自体相下的总能量,
、
、
、
分别表示Fe原子、Mn原子、Cr原子、Al原子的总能量。
由表1可知,FeMnCrAl合金在结构I和II下具有负的形成能,而结构III下具有正的形成能;表明可容易制备具有结构I和II的FeMnCrAl合金,而不容易制备具有结构III的FeMnCrAl合金。FeMnCrAl合金在三种结构下都具有正的结合能,表明三种结构的FeMnCrAl合金一旦制备,都可以稳定的存在。
3.2. 磁性
在表1,给出了四元全Heusler合金FeMnCrAl在三种结构下的原胞总磁矩、各个原子的磁矩。在结构I中,原胞总磁矩、各个原子的磁矩都为零;表明结构I下,FeMnCrAl合金是顺磁体。当FeMnCrAl合金具有结构II时,Fe、Mn、Cr、Al原子的磁矩分别为0.251、−2.636、2.170、0.033 μB,Mn原子的磁矩与最近邻的Fe原子、Cr原子的磁矩反平行;表明结构II下,FeMnCrAl合金具有反铁磁性。结构II-FeMnCrAl合金的原胞总磁矩为−0.002 μB,很好的符合Slater-Pauling规律,从而可能具有半金属特性。结构III-FeMnCrAl合金的原胞总磁矩为0.026 μB,明显的偏离Slater-Pauling规律;Fe、Mn、Cr、Al原子的磁矩分别为2.566、−0.762、−1.615、0.018 μB,Fe原子的磁矩与最近邻的Mn原子、Cr原子的磁矩
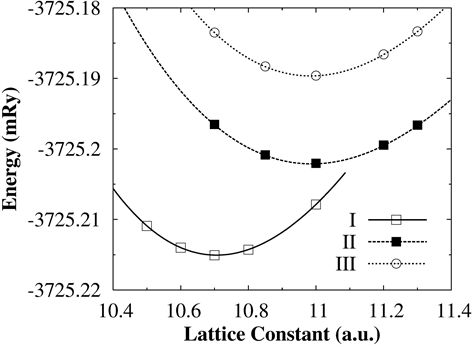
Figure 2. Variations of total energies with respect to lattice parameters
图2. 总能量随晶格常数的变化曲线

Table 1. Optimized lattice constant (Å), total magnetic moments per unitcell and atomic magnetic moments (μB), formation energy and cohesive energy (eV)
表1. FeMnCrAl在不同结构下最优化晶格常数(Å)、原胞总磁矩与各个原子磁矩(μB)、形成能ΔH(eV)与结合能ΔE(eV)
反平行;表明类似于结构II下,结构III--FeMnCrAl合金也表现出反铁磁性。
3.3. 电子结构与半金属特性
图3中给出了四元全Heusler合金FeMnCrAl的态密度(DOS)。对于自旋向下的态密度乘了−1,Fermi能级(EF)取为0。
从图3可以看出,结构I-FeMnCrAl态密度在自旋向上和自旋向下对称分布,表明此结构中自旋向上的电子数与自旋向下的电子数相等,即合金的净磁矩为零,为顺磁性合金,此结果与磁性的讨论一致。结构II-FeMnCrAl的自旋向上的能带在EF附近具有带隙,此时EF位于能隙的边缘,表现出类似于半导体特性;而自旋向下能带在EF处具有有限态密度,即呈现出金属性。因此,结构II-FeMnCrAl具有准半金属特性,具有很高的自旋极化率P(91%),P = (N↑ − N↓)/ (N↑ + N↓),其中N↑和N↓分别表示EF处自旋向上和自旋向下能带的态密度。与此相反结构III − FeMnCrAl具有传统铁磁体的态密度曲线,即EF处自旋向上和向下能带非对称分布,具有不同的态密度值,它的自旋极化率为78%。
借助能带结构图,可以理论上解释Slater-Pauling规律,即Mtot = Ztot − 24,其中Ztot为原胞中总的价电子数目。图4给出了结构II下FeMnCrAl的自旋向上能带结构。从图4可以看到,填充自旋向上能带的电子数(n↑)为12,其中有1个s电子、4个p电子和8个d电子,因此有n↓ = Ztot − 12个电子将填充自旋向下能带,所以总自旋磁矩Mtot = | n↑ − n↓| = Ztot − 24,即为Slater-Pauling规律,此规律给出了一种探索半金属材料的有效途径。
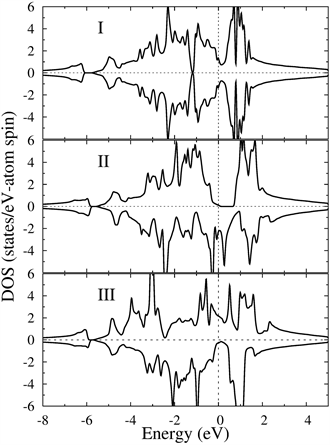
Figure 3. Total density of states of FeMnCrAl for I, II, III-structures
图3. 结构I、II、III下FeMnCrAl的总态密度
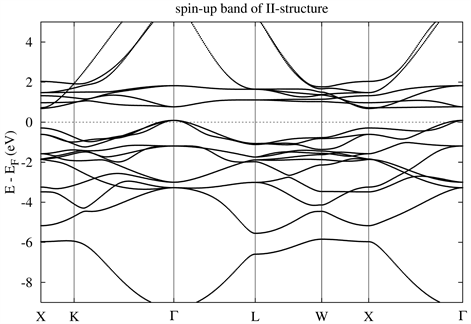
Figure 4. Spin-up band of FeMnCrAl with II-structure
图4. 结构II下FeMnCrAl的自旋向上能带结构
4. 结论
利用全势线性缀加平面波方法,结合广义梯度近似,研究了全Heusler合金FeMnCrAl的电子结构、磁性及半金属特性。按照原子的不同排列方式,采用了I,II,III等三种可能的晶格结构。计算结果表明:结构I-FeMnCrAl合金的能量最低,表现出顺磁性;结构II属于亚稳态,原胞的总磁矩为−0.002 μB,很好的符合Slater-Pauling规律,Mn原子的磁矩与最近邻的Fe原子、Cr原子的磁矩反平行,具有准半金属特性,它的自旋极化率为91%;结构III的能量最高,原胞总磁矩为0.026 μB,明显的偏离Slater-Pauling规律,Fe原子的磁矩与最近邻的Mn原子、Cr原子的磁矩反平行,表现出传统的亚铁磁性,具有较低的自旋极化率(78%)。
基金项目
感谢国家自然科学基金(11264041)的支持。