1. 引言
“十一五”期间,我国环境保护取得了令人可喜的成绩,特别是空气污染物这项指标超额完成规划目标。但是我国环境形势任然很严峻,根据耶鲁大学公布的全球环境绩效指数(EPI)报告显示,中国GDP总量从2006年的第四名上升到目前第二名并稳居第二名,然而环境绩效指数却从2006年的第94名(参评133个国家)下降到2016年的倒数第2名,其中空气质量是拖后中国排名的最主要的原因 [1] [2] 。中国用40年的时间基本上完成了发达国家100多年的城市化进程,却也只用30多年的时间“集聚”和“爆发”了发达国家100多年的环境问题。如果中国解决不好当前我国的环境问题,不但会严重影响社会经济的可持续发展,还可能影响到政府执政的公信力。
在国家环保局发布的文件《国家环境保护“十三五”规划基本思路》中就初步提出了2020年及2030年两个阶段性目标——到2020年,PM2.5超标30%以内城市必须实现PM2.5年均浓度达标。到2030年,要实现全国城市环境空气质量基本达标,生态环境质量全面改善,生态文明水平全面提高 [2] 。
因此,了解并掌握空气污染物背后的成因,计算出每种污染物对于空气质量的贡献以及分析各污染物背后成因,不仅方便城市进行针对性整治,也能促进每座城市的生态文明建设。进一步,计算出每座城市能否完成以及该如何调整发展模式才能完成“十三五”规划的目标,不仅能方便各座城市及时调整城市规划的目标,还能加快中国环境治理和改善的进程,具有重大的现实指导意义。
2. 各大城市大气污染物浓度及其趋势预测
2.1. 各大城市大气污染物浓度值
因为大气污染浓度与工业产值,经济发展具有很重要的关系,因此本文主要以一线城市包括北京,上海,广州,深圳,以及新一线城市成都,杭州,武汉,天津,南京,重庆,西安,长沙,青岛,沈阳,大连,厦门,苏州,宁波和无锡共十九个城市为代表进行研究。
首先从中国空气质量在线平台(https://www.aqistudy.cn/)搜集各大城市历史空气质量指数AQI以及各大空气污染物的每月数据。但为了把保证预测精度,我们以每季度的平均值进行分析,因为每年相同季度的各污染物的值的波动范围大致是相同的。每季度的数据如表1所示(以北京市为例,其余见附件一):

Table 1. The concentration of air pollutants in Beijing in recent years (excerpt)
表1. 北京市近年来各季度大气污染物浓度值(节选)
2.2. 各大城市按照其污染程度分类
AQI (Air Quality Index)是空气质量指数定量描述空气质量状况的无量纲指数。其数值越大、级别和类别越高,说明空气污染状况越严重,对人体的健康危害也就越大。
AQI的计算公式如下:
其中IAQI——空气质量分指数,n——污染物项目。且
IAQIP——污染物项目P的空气质量分指数;
CP——污染物项目P的质量浓度值;
BPHi——相应地区的空气质量分指数及对应的污染物项目浓度指数表中与CP相近的污染物浓度限值的高位值;
BPLo——相应地区的空气质量分指数及对应的污染物项目浓度指数表中与CP相近的污染物浓度限值的低位值;
IAQIHi——相应地区的空气质量分指数及对应的污染物项目浓度指数表中与BPHi对应的空气质量分指数;
IAQILo——相应地区的空气质量分指数及对应的污染物项目浓度指数表中与BPLo对应的空气质量分指数。
其数值与空气质量分类的关系如表2所示。
因此我们基于各大城市近年来各月份AQI的平均值,先大致对城市归为如下两类:
第一类:AQI位于50~100 (二级良)的城市:
上海 广州 深圳 杭州 南京 重庆 长沙 青岛 大连 厦门 苏州 宁波 无锡
第二类:AQI位于101~150 (三级轻度污染)的城市:
北京 武汉 成都 天津 沈阳 西安
从分类结果来看,这19个城市大都处于二级,三级之中。
2.3. 各大城市空气质量指数以及各大气污染物浓度的预测
2.3.1. 灰色预测
以下运用灰度预测的方法分别对各大城市空气质量指数和各大气污染物PM2.5,PM10,SO2,CO,NO2,O3进行预测(以北京市AQI预测为例,其余见附录附件二链接) [3] [4] [5] 。

Table 2. AQI’s relation to the classification of air quality
表2. AQI的数值与空气质量分类的关系
从图1可以看出,北京市的AQI有下降的趋势。但是,从预测曲线来看,灰色预测后的趋势近乎是线性的,不太符合实际,因此接下来我们采取BP神经网络再进行一次预测,并最后将这两种方法进行误差分析选取最佳的一种的预测方法。
2.3.2. BP神经网络预测
以下运用BP神经网络预测的方法分别对各大城市空气质量指数和各大气污染物PM2.5,PM10,SO2,CO,NO2,O3进行预测(以北京市AQI预测为例,其余见附录附件二链接) [6] ,预测结果如图2所示。
从图2可以看出,BP神经网络预测结果是有一定的波动似乎是比较符合实际的。不过从AQI的预测结果可以看出。到2030年,两个方法预测值仅相差6个浓度值左右,因此有必要对这两种方法进行误差比较分析。
2.3.3. 灰色预测与BP神经网络预测误差比较分析
我们以前10个季度为样本,以后四个数据作为检测。得到两种方法预测结果和误差如图3,图4所示。
从图3和图4可以看出,虽然两者预测值相差不大,但BP神经网络预测趋势与原数据大致相同,而灰色预测则有点出入。
进一步计算出预测的平均残差可得:灰色预测:13.22,BP神经网络:6.34。
显然BP神经网络更加优于灰色预测。因此我们选用BP神经网络对城市的空气质量指数和各污染物进行预测。
2.3.4. 至2030年未能达标的城市
依据BP神经网络,我们预测出到2030年AQI仍超出100的城市有以下6个北京,武汉,天津,重庆,西安,长沙。以下我们将针对这6座城市分析其主要污染物及污染物成因。
2.4. 未达标城市的污染物与空气质量指数的灰色关联度分析
从2.3.4中我们已经得出了未达标的6座城市,以下就6座城市的空气质量指数与各污染物的数据对其进行灰色关联度分析。
2.4.1. 灰色关联度模型
STEP1:选取参考序列,这里以AQI的数据为参考序列。
(k表示时刻,
) (1)
(m为比较数列的个数) (2)
STEP2:比较各污染物的数据对AQI在各时刻的关联系数
(3)
其中
为分辨系数,一般为0.5,
,
为两级最小差和最大差。
STEP3:计算各污染物的数据对AQI的关联度。
(4)
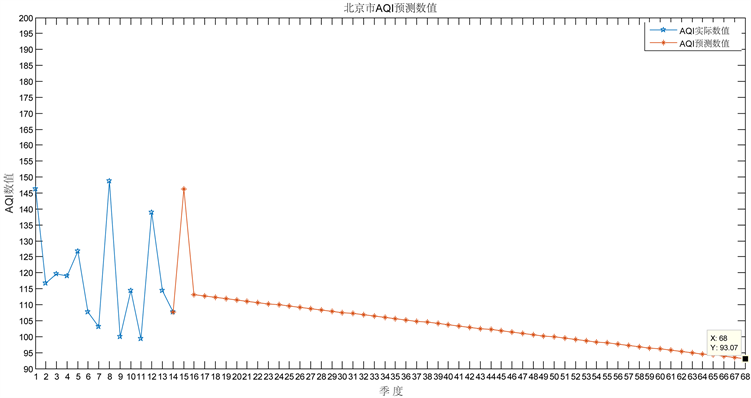
Figure 1. AQI grey prediction results of Beijing
图1. 北京市AQI灰色预测结果
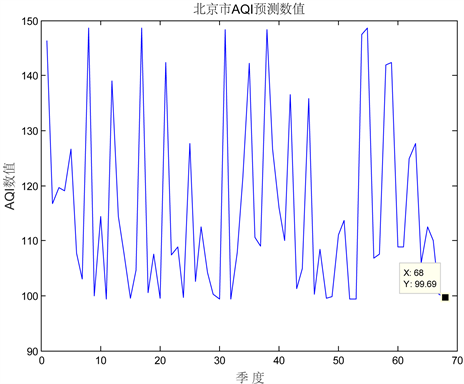
Figure 2. BP neural network prediction results of AQI in Beijing
图2. 北京市AQI的BP神经网络预测结果

Figure 3. The error test of grey prediction
图3. 灰色预测的误差检验
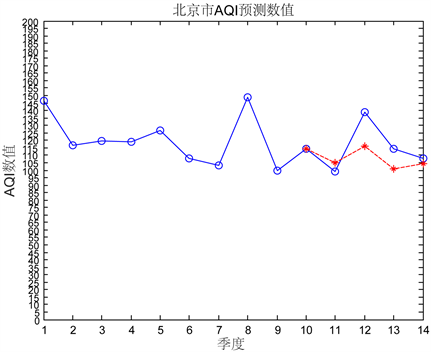
Figure 4. Error test of BP neural network
图4. BP神经网络的误差检验
2.4.2. 未达标6座城市各污染物浓度与AQI的关联度
通过MATLAB2014a编程得到,未达标6座城市各污染物浓度与AQI的关联度的表格如表3。
从表3可以看出,北京,天津,重庆,西安主要污染物是PM10,而武汉主要污染物浓度是CO,长沙主要污染物浓度是SO2。
3. 未达标城市的主要污染物的成因分析
3.1. 污染物成因的指标的确定
为了研究不能达标的六座城市的主要污染物的成因,以便针对主要成因对点治理,现对空气污染物

Table 3. Correlation between the concentration of pollutants and AQI in 6 cities
表3. 未达标6座城市各污染物浓度与AQI的关联度
提取一个总的成因指标。查阅文献 [7] 知,影响空气污染物原因主要可分为如下几种:规模以上能源消费总量(万吨);各城市的GDP(亿元);各城市的机动车保有量(辆);绿化城市的覆盖率(公顷/立方千米);工业废气排放量(亿立方米);烟粉尘排放量(万吨);查阅各城市的统计年鉴,便能得到上述指标的值,见附录附件3。
3.2. 各城市主要污染物的主要成因分析
以北京为例,对北京市的主要PM10进行成因分析。查阅文献 [8] 知,可以采用最小二乘回归和主成分分析两种方法进行分析,下文便分别采用这两种方法进行分析,并最后通过误差检验来比较两种方法的优劣。
3.2.1. 最小二乘回归
最小二乘回归法又称最小平方法,它是通过调整回归系数使得回归方程与实际数据之间误差的平方达到最小 [9] [10] 。其模型如下:
其中
为回归预测值,
为回归系数,a为回归方程的常数项。
采用最小二乘回归对北京主要污染物PM10进行成因分析得到回归方程如下:
从系数的绝对值的大小可以看出,北京市主要污染物PM10的主要成因是城市绿化面积覆盖率和烟粉尘排放量。可见城市绿化面积覆盖率会降低北京市主要污染物PM10的浓度,而工业烟粉尘排放量则会升高北京市主要污染物PM10的浓度。进一步求出均方误差如下:
3.2.2. 主成分分析
主成分分析也称主分量分析,旨在利用降维的思想,把多指标转化为少数几个综合指标(即主成分)。降维后的主成分能涵盖原信息的大部分信息 [11] [12] 。其步骤的程序框图如图5所示;
采用主成分分析法对北京主要污染物PM10进行成因分析得到回归方程如下:
其中选取的主成分个数为4,从系数的绝对值大小可以看出,主要成因仍是北京市主要污染物PM10的
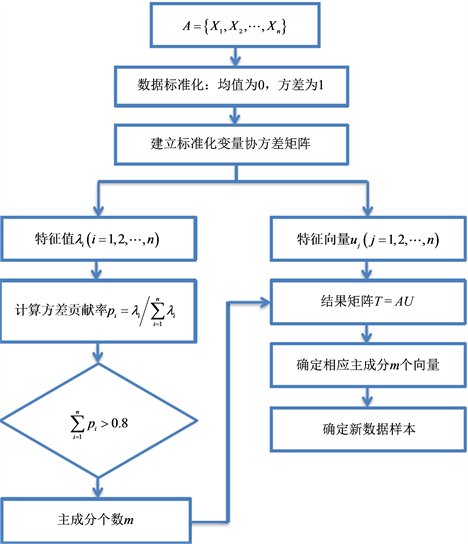
Figure 5. Flow diagram of principal component analysis
图5. 主成分分析程序框图
主要成因是城市绿化面积覆盖率和烟粉尘排放量。进一步算出均方误差如下:
3.2.3. 综合分析
从均方误差可以看出。主成分分析的结果更加准确。因此对北京市的PM10的成因分析采用主成分分析法,得出北京市主要污染物PM10的主要成因是城市绿化面积覆盖率和烟粉尘排放量。相似的,对于其他城市,可以得出:
天津市主要污染物PM10的成因分析采用最小二乘法回归更好,其中回归方程为:
因此天津主要污染物PM10最主要的影响因素是城市的绿化面积覆盖率。
重庆市主要污染物PM10的成因分析采用主成分分析法更好,其中得到的回归方程:
其中可看出重庆市主要污染物的主要因素是城市绿化面积覆盖率和烟粉尘排放量。
西安市主要污染物PM10的成因分析采用最小二乘法回归更好,其中得到的回归方程:
其中可看出西安市主要污染物最主要的影响因素有三个:机动车保有量,城市绿化面积覆盖率和烟粉尘排放量,其中机动车保有量和烟粉尘排放量有助于PM10的增长,而城市绿化面积覆盖率则能降低PM10。
武汉市的主要污染物CO的成因分析采用最小二乘法回归更好,其中得到的回归方程:
注:
代表的是固废综合利用率,因武汉市统计年鉴新增了该数据,因而多加了一个自变量。
通过回归方程可以看出影响武汉市的CO浓度最主要因素是城市绿化面积覆盖率,烟粉尘排放量和固废综合利用率,其中城市绿化面积覆盖率和固废综合利用率的提高都能显著降低CO的浓度,而烟粉尘的排放量的增高则有助于提高CO浓度。
长沙市的主要污染物SO2的成因分析采用主成分分析法更好,其中得到的回归方程:
其中可以看出长沙市主要污染物SO2最主要的影响因素城市绿化面积覆盖率,烟粉尘排放量和固废综合利用率,其中城市绿化面积覆盖率和固废综合利用率的提高都能显著降低SO2的浓度,而烟粉尘的排放量的增高则有助于提高SO2浓度。
从这上述七座城市可以看出城市绿化面积覆盖率都是影响各城市主要污染物浓度的最主要的因素,这说明这七座城市绿化面积覆盖率的提高远不能和他们所排放的污染物浓度相匹配,这七座城市应还在城市绿化面积上继续下功夫。
4. 结语
本文综合运用灰色预测,BP神经网络的方法对全国的一线城市和新一线的城市的的空气质量状况到2030年进行了一个预测,并依照至2030年不能达到国家规定的标准挑选出了六座城市,并对这六座城市运用灰色关联度的方法挑选出了其最主要的污染物,并就其主要污染物运用主成分分析和最小二乘回归的方法找出了主要污染的主要成因和其中的量化表达式,这将对每座城市的环境治理起重要的参考作用。本文所用的方法多样且进行了相互对比确保了所得结果和结论的准确性,另外本文的一个最大的不足之处便是没有对污染物的主要成因落实到具体的行业或具体的公司、工厂上去,这也将是今后一个主要的研究方向。
基金项目
1) 华中师范大学2017年度大学生创新创业训练计划B类项目;
2) 上海市青锐环境数据有限公司科研立项资助。
附录
1、附件1:各一线城市和新一线城市各季度空气污染物数据统计表: https://pan.baidu.com/s/1oDAsS3t2YM0xT2nDQAQjTA
2、附件2:各城市空气质量状况预测结果汇总(图像需用MATLAB打开):
https://pan.baidu.com/s/1kAs2o4NEgtG7D7hOLTcXVQ
3、附件3:6座未达标城市的城市环境统计年鉴网址:
北京:http://www.bjstats.gov.cn/nj/main/2016-tjnj/zk/indexch.htm
天津:http://www.stats-tj.gov.cn/Article/List/List_29.html
西安:http://tjj.xa.gov.cn/ptl/def/def/index_923_6528.jsp
长沙:http://www.cstj.gov.cn/tjnj/index.jhtml
重庆:http://www.cqtj.gov.cn/tjsj/shuju/tjnj/
武汉:http://www.whtj.gov.cn/downlist.aspx