1. 引言
纳米颗粒增强复合材料由分散颗粒和基体构成,这类材料的弹性模量、疲劳强度以及抗磨损能力等都有了较大的提高,是极具应用前景的工程材料,它被广泛应用于高端科学与工程领域中。复合材料形变初期会引起颗粒与基体之间界面的脱粘损伤,这些损伤会严重影响材料的总体性能,复合材料的细观结构损伤机理决定了它的总体力学性能。为了确立材料的细观结构与力学性能之间的联系,需要建立合理的细观力学模型来分析其有效性能和损伤过程,在材料模型中,预测材料的热机械反应规律是一个极重要的问题。
目前主要研究了由两种成分组成的复合材料,当一个增强体发生损坏时,它的承载能力会减少。Cho [1] 研究了椭圆形增强颗粒嵌入于无限体中时,增强颗粒的初始完整状态及发生损坏时的弹性应力分布情况。Thogo [2] 提出了一种增值损坏理论用来描述增强颗粒的破坏损裂情况。Asakawa [3] 主要研究了在不同荷载下增强颗粒在复合材料中发生脱粘情况时的弹性应力分析。一些方法理论例如均匀化法就是来评估以上情况发生时的复合材料的力学性能,Zhao和Weng [4] 计算了两相横观各向同性复合材料中球形增强颗粒在发生部分脱粘和完全脱粘这两种情况时的有效弹性模量系数。
然而,关于包含多相增强颗粒的复合材料研究理论少之又少。Hu [5] 建立了包含了两种类型球形夹杂的完整复合材料的模型,并研究了增强颗粒发生断裂时的作用,研究中没有分析复合材料中基体与颗粒的微观动态,因此,此模型不适用于研究热荷载下的复合材料细观研究问题。为了分析界面相的影响,Christensen和Lo [6] 研究了两种类型复合材料有效剪切模量的模型,第一种模型是宏观各向同性包含球形颗粒夹杂,且此模型是三相的:球形夹杂、基体、界面相。
Bian和Wang [7] 主要研究了颗粒复合材料的细微观组织结构力学性能,描述基体与增强颗粒界面脱粘损伤、颗粒体积分数以及颗粒尺寸对材料损伤行为的影响。Bian和Cheng等 [8] 建立了包含基体、夹杂颗粒和界面的三相复合材料模型,此界面相具有不同于基体和颗粒的刚度模量,推导出复合材料各组分材料的平均应力应变关系。目前,关于复合材料在热机械荷载作用下发生逐步脱粘时,研究材料的细观本构关系的研究不多。本文根据细观力学相关理论,在考虑温度变化因素的前提下,推导纳米颗粒复合材料中增强颗粒在外部荷载作用下发生脱粘过程中的力学本构关系。在研究过程中本文不考虑界面相的因素,只考虑基体与颗粒间的受力关系。材料在热机械荷载作用下,复合材料中的增强颗粒会处于三种状态:完整、部分脱粘、完全脱粘。文中主要研究在这三种状态下的复合材料基体与颗粒的细观力学本构关系,根据所推导的表达式,带入材料系数得到相关计算图表,并与实验数据相比较,分析讨论新理论可行性。
2. 复合材料的本构关系
在外荷载作用以及温度变化情况下,随着复合材料发生形变,由于增强颗粒脱粘损伤及基体内部孔洞的出现,材料的弹性性能会因此减弱。因此损伤后复合材料的弹性模量、体积模量和剪切模量将不能再用未损伤的材料模量表示,需采用“有效弹性模量”这一概念描述复合材料损伤后的力学性能。
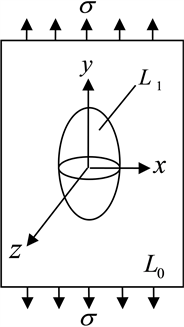
调查研究显示单向对齐颗粒的显微结构(例如形状以及体积分数)和损坏方式产生对复合材料的有效热响应以及力学响应的影响 [9] [10] [11] [12] 。如图1所示,纵横比l的增强颗粒,在一定的负载限度内,增强颗粒受高应力的作用产生破裂或者脱粘情况。因此,增强颗粒的平均应力在发生破裂和脱粘的时候将会完全释放出来。诚然,增强颗粒的承载能力随着其平均应力释放而减少。图1表示,在无限大弹性体内的椭圆形增强颗粒受外部应力s的情况,根据Eshelby’s等效夹杂方法,椭圆形的增强颗粒承载应力是均匀的并且表达式为 [13] [14]
(1)
式中L0——基体弹性刚度张量;L1——增强颗粒弹性刚度张量;S——Eshelby’s张量,为颗粒形状与基体材料泊松比的函数;I——单位刚度矩阵。
Cho [1] 用有限元方法研究了一个椭圆形颗粒沿着xy-平面发生断裂时的应力分布以及平均应力,如图1(b)所示。然而,损坏颗粒的应力分布是非常复杂的,它的平均应力表达式可以如下表示 [13] [14]
(2)
式中σp——完整颗粒的承载应力;k——损坏颗粒平均应力与完整颗粒承载应力之间的关系系数。
σcp——损坏颗粒的平均应力,若应力写成如下的矩阵形式,
(3)
 (a)
(a) (b)
(b)
Figure 1. (a) Loading case of intact particle; (b) Loading case of debonding particle
图1. (a) 基体中完整颗粒受力情况;(b) 基体中脱粘颗粒受力情况
则椭圆形颗粒的有效系数k以矩阵形式表达 [13] [14] ,
(4)
矩阵中三个系数h13,h33,h44是包含夹杂颗粒纵横比以及夹杂颗粒与基体弹性模量的函数。这里的颗粒可以是扁平形状或者扁长形状,也可以是球形的。
在复合材料中,基体发生的应变是弹塑性的,而增强颗粒一般是发生弹性应变。根据胡克定律,可以得出基体和增强颗粒的应力应变关系 [9] ,
(5)
当i为0时表示基体,1时表示增强颗粒。
式(5)中
——弹性刚度张量;Ei——杨氏模量;νi——泊松比;T——温度;Ni——温度膨胀系数。
其中,
(6)
式中δij——克罗内克函数。对于正应力关系式
,对于剪切应力
。
对于基体的弹塑性变形,可以用普朗德尔罗斯方程写成接近于弹性变形的形式 [9]
(7)
式中
是由式(5)中
的E0和ν0分别换成
和
得出的。
和
是弹塑性变形下的杨氏模量和泊松比 [9] ,
(8)
其中
——基体的变形硬化比。
(9)
式中σe——冯’米塞斯等效应力;ξe——冯’米塞斯等效应变。公式(7)只能应用于单调比例荷载的情况。
在本文的分析研究中,复合材料中基体相和颗粒相的体积含量分别为C0和Cp,有
。在损伤过程中,完整颗粒、部分脱粘颗粒与完全脱粘颗粒的体积含量分别记作C1,C2和C3。根据Eshelby的等效变换理论和Mori-Tanaka的均匀化方法,可以得出复合材料中基体、完整颗粒、部分脱粘颗粒以及完全脱粘颗粒的应力表达式,基体的平均应力应变关系式 [9] ,
(10)
式中
——基体的平均弹性应力;
——复合材料的应力;
——扰动应力(基体与纯基体材料的应力差);
——基体平均弹性应变;
——复合材料的平均应变;
——扰动应变(基体与纯基体材料的应变差)。
完整颗粒的平均应力应变关系表达式,
(11)
式中
——完整颗粒平均应力;
——基体与完整颗粒在荷载作用下产生的扰动应力;
——基体与完整颗粒在荷载作用下产生的扰动应变。
部分脱粘颗粒的平均应力应变表达式 [13] [14] ,
(12)
式中
——基体与部分脱粘颗粒产生的扰动应力;
——基体与部分脱粘颗粒产生的扰动应变。其中
,
同理可得出完全脱粘颗粒的应力应变表达式 [13] [14] ,
(13)
式中
——基体与脱粘颗粒产生的扰动应力;
——基体与脱粘颗粒产生的扰动应变。其中
。
在公式(11),(12)和(13)中,
是Eshelby等效转换应变,且有
(14)
(15)
同时扰动应变
可以转换成Eshelby等效转换应变
,
(16)
其中r = 1,2,3,S——Eshelby张量。因此,
(17)
这里可以写出复合材料的平均应力
,以及扰动应力
的表达式
(18)
(19)
I是四阶单位矩阵。把式(15)和(17)代入到式(19)中可得出扰动应变
的表达式,
(20)
综上,式(16)和(20)代入到式(11),(12)及(13)中,则可以求出Eshelby等效转换应变
的表达式,
(21)
(22)
(23)
以上公式中:
复合材料的平均应力
可以写成如下形式,
(24)
复合材料平均应变
也可以求出,
(25)
把式(16)和(20)代入上面式(25)中,可得出
与
的关系式,
(26)
其中
(27)
(28)
式中
——因外部荷载引起的应变;
——颗粒脱粘引起的应变;
——温度变化引起的应变。
由式(10)可以得出基体的平均应力,
(29)
进一步,可以由得出完整颗粒与脱粘颗粒的平均应力,
(30)
3. 数值分析与实验对比
首先,为了证明所得的本构关系合理性,与其他一些研究结果进行比较。如图2所示,ROM [9] 方法得出的热膨胀系数与本文中得出的热膨胀系数作比较,其中复合材料基体与增强夹杂分别是环氧基树脂和玻璃。
从图2可以看出,复合材料的热膨胀系数上限是从ROM [9] 方法得出,下限是从Reuss [9] 方法中得出的,而用Kerner [9] 方法得出的结果比Reuss的结果更接近于本文方法得出的热膨胀系数。本文方法得

Figure 2. Relationship between the thermal coefficient and particle volume fraction of composites
图2. 复合材料热膨胀系数与增强颗粒体积分数的函数关系
出的热膨胀系数是介于Reuss方法与ROM方法结果中间。相比于ROM的结果,Kerner方法得出的结果更接近于本文方法得出的结果。
举例说明本文得出的本构关系表达式,基体材料选择铝(Al),增强颗粒材料选择陶瓷(PSZ),其在不同温度下的温度膨胀系数以及力学性能参数如表1所示。
对于弹塑性分析,基体的等效应力与等效塑性应变关系有以下关系,
(31)
式中:σ0——基体屈服强度。
图3表示用基体材料标准化的有效热膨胀系数与不同纵横比λ增强颗粒体积分数的函数关系。在这里研究的复合材料是增强颗粒比基体材料更硬的情况。这时,复合材料标准化的热膨胀系数会随着增强

Table 1. Thermal coefficient and mechanical properties of materials under different temperatures
表1. 不同温度下材料的温度膨胀系数以及力学性能参数

Figure 3. Relationship between the thermal coefficient α/α0 and particle volume fraction Cp
图3. 标准化热膨胀系数α/α0与增强颗粒体积分数Cp的函数关系
颗粒纵横比与体积分数减小而更大。
图4表示在不同的增强颗粒体积分数及λ=1的条件下,损坏演变过程与标准化热膨胀系数的函数关系。图5表示标准化热膨胀系数与不同纵横比颗粒损坏演变的曲线关系。这些图显示出了增强颗粒体积

Figure 4. Relationship between the damage process and standard thermal coefficient
图4. 损坏演变过程与标准化热膨胀系数的函数关系
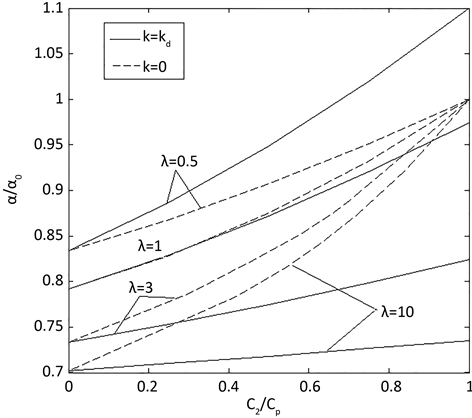
Figure 5. Relationship between the standard thermal coefficient and particle damage process
图5. 标准化热膨胀系数与不同纵横比颗粒损坏演变的曲线关系
分数与颗粒的纵横比对标准化热膨胀系数的影响,当所有增强颗粒发生脱粘损坏时,复合材料的热膨胀系数接近于基体的热膨胀系数,而且颗粒的体积分数越低复合材料热膨胀系数接近度越高。这是因为当增强颗粒发生脱粘时,它的承载能力会减小,直到增强颗粒完全脱粘变成空洞,它的承载能力会消失,因而复合材料中几乎只有基体的影响。同时,当增强颗粒的热膨胀系数小于基体时,复合材料标准化热膨胀系数会随着增强颗粒体积分数增大而减小,此外,标准化热膨胀系数随着增强颗粒纵横比的增大而减小。
图6表示在不同k-矩阵情况下温度对α0/α与颗粒损坏演变的影响曲线(λ = 1)。从图6中可以发现温度因素对完整、部分脱粘及完全脱粘这三种不同状态下的增强颗粒发生损坏时与复合材料标准化热膨胀系数的曲线关系,其中初始颗粒体积分数0.4,增强颗粒的纵横比1。由图6发现,标准化热膨胀系数随着温度的升高而减小。对于完整颗粒复合材料,由于复合材料中增强颗粒一直是完整的,所以标准化热膨胀系数取恒定值,不会随着温度改变而产生变化。而在颗粒最终完全脱粘情况中,复合材料热膨胀系数会随着颗粒发生完全脱粘逐步趋向于基体热膨胀系数值。对于部分脱粘情况,因为增强颗粒最后都会部分脱粘,曲线总体趋势是与完全脱粘时是差不多的,这时的曲线位于完全脱粘与完整情况之间。由图6看出,温度对复合材料热膨胀系数的影响,所以要想得到关于复合材料力学性能更准确的结果,温度因素是必需要考虑的。
为了验证本文推导的复合材料热膨胀系数关系式的合理性,在这里我们用如下性能的各向同性复合材料做模拟计算。
体积模量K1 = 15.6 GPa、K0 = 4.7 GPa,
剪切模量G1 = 11.7 GPa,
热膨胀系数α0 = 0.1 × 10−6/k。
假设材料是各向同性,增强颗粒是定向分布以及颗粒的纵横比取50,以上前提下所得出的材料温度膨胀系数曲线如图7所示。图7表明本文所预测的复合材料的体积模量和剪切模量以及其温度膨胀系数

Figure 6. Curves of the temperature versus α0/α and particle damage process under different k-matrices
图6. 在不同k-矩阵情况下温度对α0/α与颗粒损坏演变的影响曲线
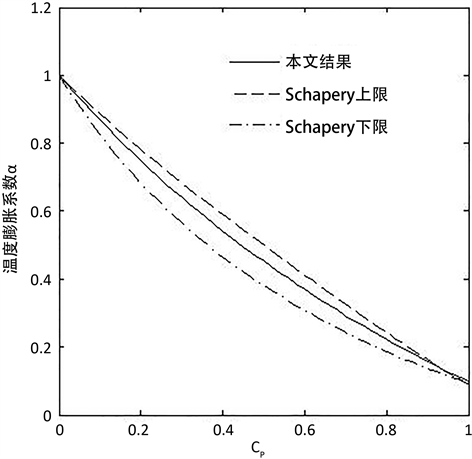
Figure 7. A comparison of temperature expansion coefficients of composites
图7. 复合材料预测温度膨胀系数的比较
都在前人 [9] 实验测量范围内浮动。由此可见本文结果具有一定的合理性,同时图7表示温度膨胀系数α与增强颗粒体积分数CP之间的变化关系。
4. 结论
本文以细观力学的方法,建立了纳米颗粒增强复合材料细观损伤破坏模型,推导出了纳米颗粒复合材料在外部应力作用下各组分材料的本构关系表达式。以此为基础,分析讨论了温度变化与材料本身以及相关参数之间的关系。从计算结果可知,复合材料中颗粒发生脱粘情况时,它的热膨胀系数受增强颗粒体积分数、颗粒的纵横比以及温度变化的影响。标准化热膨胀系数与颗粒体积分数及纵横比形成鲜明的反比关系,而标准化热膨胀系数随着温度升高而减小。对于整体复合材料中颗粒发生脱粘损坏的情况,材料的热膨胀系数上下限由完整颗粒以及完全脱粘颗粒状态下给出。
基金项目
河北省高等学校科学研究重点项目基金,编号:ZD2017075。