1. 引言
随着我国综合国力的提升,现代化建设进程不断加速,超高墩、柱的桥梁急速增多,从而导致桥梁坍塌事故近年来频繁爆发,如2012年,江西广昌一大桥发生垮塌,四名伤者因抢救无效死亡;2012年哈尔滨机场高速主桥最后一段被四辆重货车压塌,坍塌事故造成数人死亡;2007年美国苏达州跨河大桥突然倒塌,导致5人死亡,30多人失踪。针对桥梁的变形进行有效监测,能够降低桥梁坍塌事故发生对于人民生命和财产的威胁,因此针对桥梁的变形监测具有极其重要的意义。
变形是指工程或建筑物随着时间的变化而发生的形状或位置的改变,而变形数据的分析总的来说就是为对变形信号进行分析。处理变形监测数据的方法主要有回归分析模型、灰色系统理论分析模型、时间序列分析模型、趋势分析法、模糊线性回归分析法等 [1] 。小波分析是在傅里叶变化的基础上发展起来的一种时频分析方法。它可以利用小波基函数将时间序列分解为低频和高频分量,然后在不同的尺度上对高频和低频分量进行研究。对处理如变形监测数据等的非平稳的信号极其适合。
小波分析是1986年由著名数学家Y. Meyer、S. Mallat合作构建基本小波基后,才蓬勃发展起来的 [2] 。自20世纪90年代以来,小波分析开始运用于测绘领域,其最早是用于影像检测。在这一时期,小波变化被运用于摄影测量与遥感方面,研究影像的文理特征等。Collin F.和Warrant R.将小波分析运用于GPS数据处理。1999年,小波分析被运用于精密工程测量方面,用于确定地球的重力潮汐参数精度等。现在,小波分析的方法已经渗透到地球物理探测、语音信号处理、神经网络以及工程计算等各个领域。目前,小波分析在处理测量数据方面的运用主要有:基于小波分析法检测GPS相位观测值,变形信号提取以及基于小波变换的变形检测数据处理探测周期性信号等 [3] 。近十年来,研究人员又相继提出改进后的小波滤波处理数据的方法,并取得了不错的成果。史连艳和杨树兴(2006)先后采用了中值滤波后小波滤波处理变形监测的数据 [4] ;Li and He (2006)采用改进的小波包单阈值处理方法。卞继承(2012)利用中值滤波和小波滤波相结合的方法进行数据去噪 [5] 。
从已有变形监测数据的处理方式来看,对于复杂的变形监测数据进行分析,单纯的数据处理方法已不再适用。小波分析作为目前分析处理信号的最简单有效的工具,在去噪方面具有优势。本文主要以某实际工程项目的变形监测为基础,采用小波分析法作为变形监测数据的处理的基本工具,并结合工程中的实际情况,研究数据的特征,建立基本的模型,对数据进行处理分析,并在分解信号、去噪、精度评定等方面进行研究。
2. 研究区概况与研究方法
2.1. 研究区概况
西部大开发进程的加速,高速公路桥梁迅速增加。但四川等山区地形、地貌、地质水文等条件复杂,因而在建设过程中高墩跨度大。
本文以四川某山区在2015年新建成的公路桥为研究对象。该公路桥全长959米,宽30米。桥梁在正常运营的状态下,其形状和位置总会随着时间而发生相应的变化。测量的变形监测数据往往会受到一些噪声信号的影响。如风力、车载量、温度等。为获得桥梁的变形性态,测量人员在桥墩布设监测点位,进行多周期观测。由于桥梁的变形监测数据是具有噪声信号的非平稳信号,且变形监测数据具有一定的周期性,因此可以采用小波分析来处理变形监测信号。
2.2. 研究思路与方法
本文将研究小波分析的基本原理,模拟变形监测数据,建立变形监测数据处理模型,并利用MATLAB软件的小波工具箱自带的小波函数,编写相关程序,通过均方根误差、信噪比等指标来指导小波分解,提取粗差,确定最优小波基及最大分解尺度。同时研究小波阈值去噪函数,以确定最佳的阈值去噪函数。最后根据模拟实验建立的最佳模型,处理变形监测数据的实例,并对其处理结果进行分析和精度评定。
3. 变形监测数据及分析
表1为该桥梁自建成起的沉降变形的监测数据,观测时间从2015年到2016年,以每一周为一个观测周期,观测40个周期的沉降监测数据。
变形监测数据的处理包含原始数据的检查、去粗差等。图1和图2为该桥梁每一周期的累积下沉量随时间变化的曲线。从曲线可知,下沉可大致分为三个大的部分。第一部分是1~15周,此时桥梁下沉量较大;15~16周为第二部分,沉降开始大幅度回升,之后又开始缓慢下降;16~40周为第三部分,沉降量开始减小并逐渐趋向于稳定。但图中并不能看出数据的外界影响因素以及奇异点的探测,此时需要对原始数据进行小波分解,找出小波分解后的高频系数中的极值,并进行奇异点判断,并以此发现异常点。
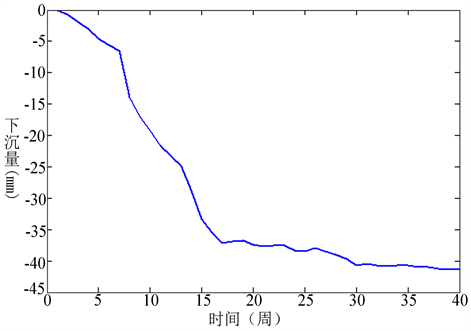
Figure 1. The accumulative total settlement changes over time
图1. 累积沉降量随时间变化曲线
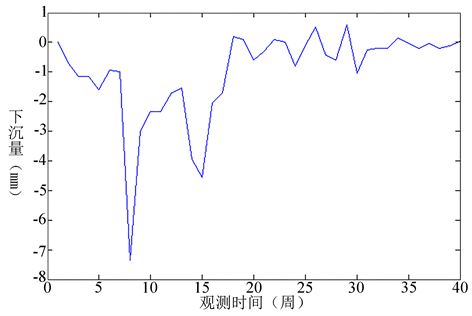
Figure 2. The speed of sinking varies with time
图2. 下沉速度随时间变化曲线

Table 1. Bridge deformation monitoring data
表1. 桥梁变形监测数据
4. 变形监测条件确定
4.1. 变形监测数据处理模型
为了确定变形监测数据处理的最佳模型,本文拟采用模拟变形监测数据的一个非平稳信号来进行实验。表达式如下:
(1)
由于变形监测的数据大多都含有噪声,故在该信号中加入方差为2的高斯白噪声。原始信号图以及加入噪声后的信号图如图3、图4所示。
4.2. 确定最大分解尺度
Db小波具有良好的正则性,n值越大,正则性就越好,即光滑性就越好,因此具有良好的分析特性。实验采用db10小波对噪声信号进行不同尺度的分解,图5、图6、图7、图8分别为非平稳信号的不同
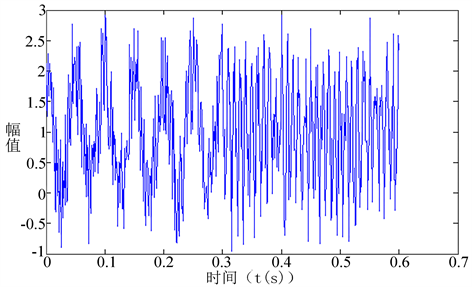
Figure 4. The signal after adding the noise
图4. 加入噪声后的信号
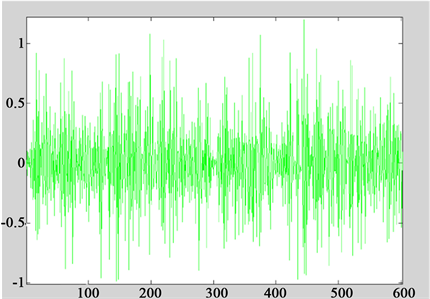
Figure 5. 1-level decomposition of non-stationary signals
图5. 非平稳信号的1层分解
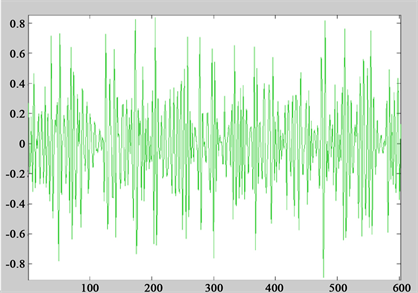
Figure 6. 2-level decomposition of non-stationary signal
图6. 非平稳信号的2层分解
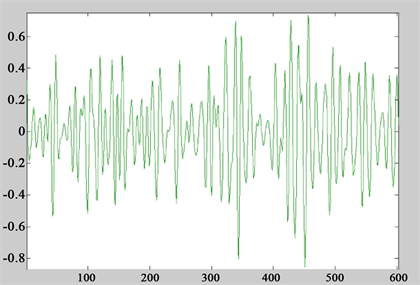
Figure 7. 3-level decomposition of non-stationary signals
图7. 非平稳信号的3层分解
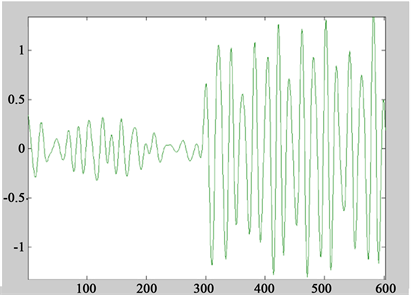
Figure 8. 4-level decomposition of non-stationary signals
图8. 非平稳信号的4层分解
分解层次结果,结果如下所示:
从表2中可以看出,当j = 2时,rk的值约为1,因此可以选择尺度j = 2或j = 3进行小波分解。从滤波后的图像来看,j = 3时,信号已经基本去掉了噪声,曲线已经接近于光滑。综上,可知最大的分解尺度为j = 3。
4.3. 最优小波基的选取
对信号进行小波分解,需要确定最佳的小波基函数。为了确定最优小波基,分别选择harr小波,db6小波,db10小波,sym6小波,coif3小波进行尺度为j = 3的分解,并计算各个小波函数去噪后的信噪比(snr),信噪比越高,去噪效果越好,以选择来最优小波基。
表3为各类小波的信噪比,通过对原始数据进行以上6种不同的小波基的小波分析后,计算其信噪比并进行比较可得db10小波的信噪比snr = 7.0084是最高的。因此,在处理变形监测数据时,采用db10小波进行分解及去噪,效果最佳。
使用db10小波对该实验数据进行三层分解去噪后的信号如图9所示。
5. 桥梁变形监测处理
5.1. 变形监测数据的粗差探测
桥梁的变形监测要受到外界因素的干扰,从而产生粗差。小波变换后,细节部分的极大值往往是函数的突变点,根据这一特点,利用小波分析进行多层次的分解,通过判断高频系数部分的极大值,进行判断,找出奇异点,从而发现异常点。根据实验结果,选择最优小波基db10小波进行j = 3的分解。
图10为原始信号的曲线图和db10小波分解后低频部分的近似信号图。图11中d1、d2、d3分别为第一层、第二层、第三层分解后的高频信号。从d1来看,t = 4,t = 5,t = 6,t = 7,t = 8,t = 10,t = 12,t = 13,t = 15处存在极值,这些点很有可能是信号的奇异点,可能是粗差。为了确定这些极值是粗差还是正常值,采用以下模型对这些点的数值进行检验 [6] 。
利用原始数据与小波三层分解后的近似信号的数据之差作为异常值检验的模型,并计算出标准差 的值,采用3 的值作为标准,若原始信号数据与近似信号数据之间的差超过3 ,则为粗差,否则则为环境变化引起的正常值 [7] 。
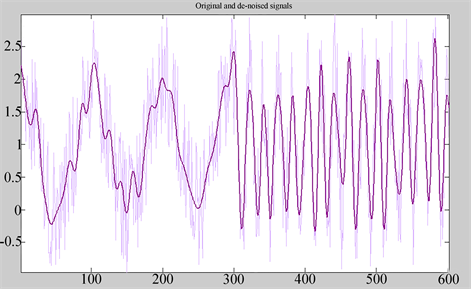
Figure 9. Raw data image and denoised data image
图9. 原始数据图像与去噪后的数据图像
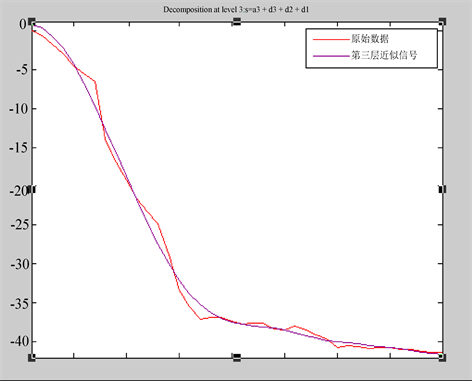
Figure 10. The original signal image and the decomposed low frequency signal
图10. 原始信号图像与分解后的低频信号

Table 2. Root mean square error at different levels of decomposition and relative changes
表2. 不同分解层次的均方根误差以及相对变化

Table 3. Signal to noise ratio of all kinds of wavelet
表3. 各类小波的信噪比
经过计算得到3s = 2.97 mm,各点的近似信号值与实测值的误差如表4所示。
从表4中可以看出,经过粗差探测可知只有7号点的误差绝对值大于3s,所以7号点为粗差点,应对其给予剔除或者修复。
在图11中,从分解的第二层高频信号d2中可以看出前16个观测周期中,有一个约为35的天的信号,这可能是由于桥梁在变形监测过程中存在一个周期性运动的力造成桥梁起伏 [8] 。从分解的d1和d2层高频系数可知,均为前20期变化较大,后期观测值的变化较小,这表示随着时间的推移,桥梁的下沉量越小。
本文将同时利用近似信号和高频部分的信号进行粗差的修正工作 [6] ,分为以下三步:1) 对原始信号进行分解,提取高频部分的系数;2) 对系数进行分析,对于系数中的奇异值进行插值,将插值结果替换该奇异值;3) 将替换后的高频系数与低频系数一起进行小波信号重构,再对重构后的信号进行去噪处理。
由图11可知,由于只有d1层的高频系数的奇异值特征显著,所以只对d1层的高频系数进行线性插值。如表5、表6、表7所示。
将插值替换后的高频系数与低频系数进行信号重构,重构后的信号如下图12所示。
粗差点7的实际值与重构后该点的值的绝对误差为1.57 mm,小于3 ,故经过插值替换后的高频系数与低频系数重构的信号已经基本上消除了粗差。利用重构后的信号进行去噪分析,效果更为理想。
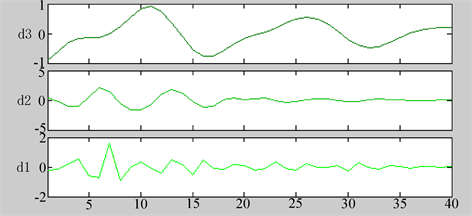
Figure 11. High-frequency information after the decomposition
图11. 分解后的高频信息

Table 4. Gross error detection results
表4. 粗差探测结果
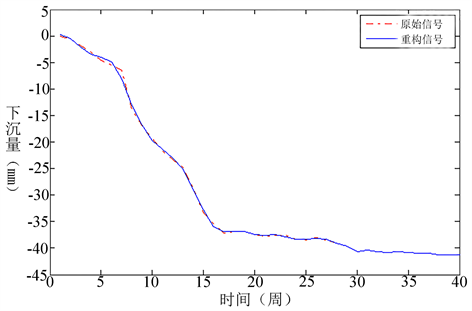
Figure 12. The original signal and reconstruction signal
图12. 原始信号与重构信号

Table 5. 4, 5 Interpolation results
表5. 4,5期插值结果

Table 6. 6, 7, 8, 10 Interpolation results
表6. 6,7,8,10期插值结果

Table 7. 12, 13, 15 Interpolation results
表7. 12,13,15期插值结果
5.2. 小波阈值去噪
对于桥梁的变形观测数据,其噪声大多集中于高频部分的系数中,比较适用采用小波阈值去噪法进行去噪。小波系数阈值化主要有软阈值去噪和硬阈值去噪两种方法。取阈值
,但无论采用哪种方法都必须确定s的值,且其值一般都是未知的。处理不同的信号,都必须选择一个最佳的分解层数才能实现最佳的去噪效果。分解层数过多,会去除许多有用信号,同时增大计算量,使得计算速度变慢。反之,分解层数过少,则不能达到很好的去噪效果 [9] 。在实际操作过程中,往往采用小波分解后第一层高频系数的标准偏差的绝对值作为s的估计值 [10] 。经过计算得到
;
。
当
时,
;当
,
。该方法为硬阈值去噪法 [11] 。采用该方法对信号进行去噪后,再重构信号,去噪后的信号如下图13所示。
经计算得硬阈值去噪后的信噪比snr = 26.3735,均方误差RMSE = 0.4709,且由于硬阈值函数含有间断点,仅仅处理小于阈值的数据,而不处理大于阈值的数据。但在实际的信号中,大于阈值的数据往往也含有着噪声数据,所以去噪效果不明显。由图13可以看出硬阈值去噪的效果并不好,图像的平滑度较低。
软阈值去噪法定义如下:当
时,
;当
,
。采用该方法进行去噪后,再重构信号,得到去噪后的信号如下图14所示。
经计算得软阈值去噪后的信噪比snr = 46.5599,均方误差RMSE = 0.0617,且由图14可以看出软阈值去噪后的信号图像已经非常接近于原始信号的图像,去噪后信号的信噪比比硬阈值去噪高,且均方根误差比硬阈值去噪的结果小,图像的平滑度较高。综上所述,软阈值去噪的效果比硬阈值去噪的效果更好。
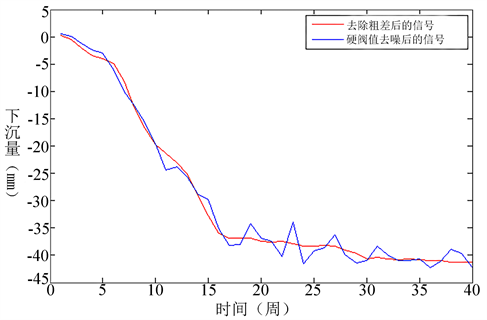
Figure 13. The signal after the gross error is removed and the hard threshold denoising.
图13. 去除粗差后的信号与硬阈值去噪后的信号
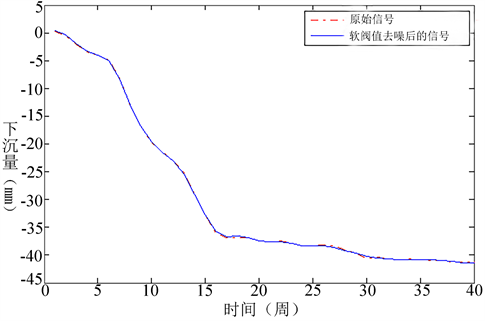
Figure 14. The signal after the gross error is removed and the soft threshold denoising
图14. 去除粗差后的信号与软阈值去噪后的信号
但软阈值法对于大于阈值l的小波系数采用固定的值来进行处理,而噪声分量与小波系数成反比,小波系数越大,噪声分量也就越小。所以采用固定的值进行处理也有一定的缺陷,去噪后的信号的小波系数与原始信号的小波系数之间存在着一定的误差。
由于硬阈值去噪存在间断点的问题,而软阈值去噪存在一定偏差。为弥补两种阈值去噪方法的不足,提出了一种改进后的阈值函数处理方法,其函数表达式如下 [12] :
(2)
由该函数表达式可知,当阈值很小时,该函数类似于硬阈值函数,但比硬阈值函数更加具有灵活性;当
接近于阈值时,并没有把小波系数变为零,而是采用渐近线逐渐趋于零,使得该函数具有连续性。当
大于阈值时,对小波系数缓慢地进行压缩,小波系数越大,压缩量就越小,当小波系数大于某一临界值时,不再对小波系数进行压缩 [13] ,这样能达到有效处理信号中存在的噪声的目的。
进行处理,处理结果如下图15所示。
各种阈值函数去噪后的信噪比(snr/db)和均方误差(RMSE)如表9所示。
通过表8可知,硬阈值去噪函数的效果最差,去噪能力最弱;改进后的阈值去噪函数去噪后信号的
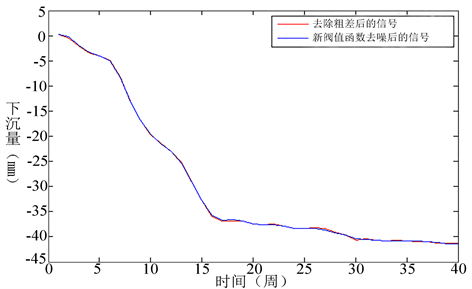
Figure 15. Remove the signal after the gross error and the signal after the new threshold denoising
图15. 去除粗差后的信号与新阈值去噪后的信号

Table 8. Signal-to-noise ratio and mean square error of various threshold functions after denoising
表8. 各种阈值函数去噪后的信噪比和均方误差
信噪比更高,均方误差更小。所以,改进后的阈值去噪函数的去噪效果比软阈值函数去噪的效果更好。
5.3. 去噪结果
通过采用改进后的阈值去噪函数对信号进行去噪效果更佳,去噪后的变形值如表9所示。
去噪后的变形监测数据如表9所示,图16为含有噪声的信号的下沉速度曲线与去噪后的信号的曲线。从图中我们可以看出,前10周,下沉速度较大,噪声比较严重。因为在这段时间内,桥梁建成没多久,是桥梁的沉降沉降较为剧烈的时候,同时由于外界因素的干扰,测量的数据中含有大量的噪声;从10周到第18周,桥梁仍然属于不稳定期,有明显的沉降,沉降数据也含有一些噪声;从19周到31周,桥梁趋于稳定,桥梁下沉速度减慢,但外界环境的干扰,仍然存在噪声;从31周到40周,由相关资料可知,此时桥梁已经试运行一段时间了,桥梁逐渐趋于稳定,测量数据中的噪声也逐渐减少。经过去噪后的信号显得更加的平滑,不仅剔除了数据的粗差,同时也基本消除了噪声的影响,使得数据变得更有规律,利于看出变形的性态和趋势。
6. 结果精度验证
经过改进后的阈值函数去噪并不能完全消除噪声,仍然含有噪声,也有些有用的信号会被当作为噪

Table 9. Deformation monitoring data after denoising (mm)
表9. 去噪后的变形监测数据(mm)
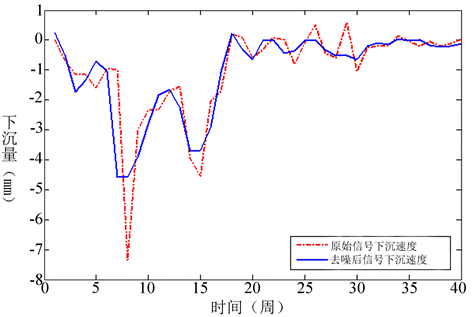
Figure 16. The sinking speed of the original signal and the sinking speed of the de-noised signal
图16. 原始信号的下沉速度与去噪后信号的下沉速度
声被剔除,因此常常采用以下标准对去噪后的信号进行评价,以确定去噪后的信号与原始数据的偏差。常用的评价指标有:信噪比(SNR) [14] 、均方误差(RMSE) [15] 、信噪比增益(GSNR)和平滑度 [16] 等。
本文采用改进后的阈值去噪函数对变形监测数据进行去噪,经过计算得SNR = 46.8592,RMSE = 0.0587,R = 0.061。相较于其它各种阈值去噪方法,改进后的阈值去噪函数信噪比更高,均方误差更小,平滑度也更高。
7. 结果分析
从图11中db10小波分解的d3层高频信号可以看出,有一个周期约为16天,振幅约为1 mm的波形,这可能是在监测的过程中存在一个周期性的力造成的结果。此外,从分解的d1,d2层高频系数的结果图来看,无论是哪一层的高频信号都是前20期的下沉量较大,因为前期受到施工等各种外界因素的影响,而后期向下沉量逐渐减小,这是由于后期桥梁逐渐趋于稳定。通过db10小波进行三层分解,并采用改进后的阈值去噪函数进行去噪,使得变形监测数据基本消除了噪声,图像显得更加平滑,更加接近于自然下沉状况,为进一步的变形分析和预测提供了依据。
从图16中,我们可以看出,噪声较大的点主要都集中在观测周期中的某些拐点上,因为在这些观测周期中,桥梁所在的地基的承受力的变化表现出急剧的变化,并且具有复杂性,此外,由于外界环境的影响,使得噪声变得更加明显。通过分析,可以找出该时间段,并为以后的工程建设提供经验和借鉴,以防止灾害事故的发生。
8. 结论
本文通过采用小波分析的方法对桥梁的变形监测数据进行处理,我们可以发现小波分析在处理含有噪声的非平稳信号方面有着其优越性,小波变换的本质就是采用与原信号相似的小波基函数来表达该信号数据。通过最优小波基函数的选取,在某个小波基函数下,用小波系数表示该信号。小波分解能够将信号分解为低频部分和高频部分,并从分解后的高频部分的系数,发现信号中的奇异值,并进行粗差探测,对于粗差进行插值,然后将修改后的高频信号与低频信号进行重构,获得去除粗差后的数据。
运用小波分析对变形监测数据进行处理时,选择不同的小波基处理信号,去噪结果是不同的。因此需要根据去噪后的结果来判断最优小波基。此外进行小波分解时,不同的分解层次可能会导致不同的去噪结果,分解层次过少,去噪效果不明显,分解层次过多,会去除一些有用的信号,增大运算量。因此需要选择最佳的分解尺度对信号进行分解。由于matlab自带的阈值去噪函数有其缺点和不足 [14] ,因此,本文采用了一种改进后的阈值去噪函数对信号进行去噪,并经过验证,去噪结果确实优于硬阈值去噪和软阈值去噪。经过小波分析处理的变形监测信号去除了粗差,基本上去除了噪声,使得变形监测数据变得更加的平滑,更加接近于自然下沉状况,为进一步的变形分析和预测提供了依据 [17] 。
本文利用小波分析处理桥梁的变形监测数据,有一定的借鉴意义,为处理含有噪声的非平稳信号有一定的参考意义。本文中还存着一些不足:小波分析选取的小波函数只是与原始信号数据具有相似性,处理的结果只能说是大体去除了噪声等影响。其次,由于桥梁的变形是一个较为复杂的过程,受到车流量、风力、滑坡等多方面因素的影响。