1. 引言
基于实际电网模型进行的电力系统仿真分析，经过对在提前设定的时间内对电力系统的特性以及行为进行研究，它是电力系统分析、决策、控制等相关内容的基础，并成为整个电力系统规划、运行及分析的重要工具。提高电力系统负荷的聚类分析准确性，我们可以深度挖掘出更多的负荷特性，针对用电侧用户的聚类分析可以挖掘出用户负荷的电力负荷模型，掌握用户的用电习惯，进一步对评估电力市场工序，指导上网电价制定具有重要意义。本文重点是根据用户在实际用电规律中对用电用户属性进行分类，结果得出，有些用户虽然隶属同一行业或相近行业，但用电负荷特存在很大差异，相反，不同行业的用户用电负荷特性往往存在高度相似性 [1] 。因此，倘若分类结果不准确，结果导致电力市场决策和需求侧评估的偏差。
聚类算法之所以受到研究学者的广泛关注，是因为现实生活中的数据集大多都是没有标记的数据。其中，比较著名的算法有基于划分的k-means算法、基于层次的CURE算法、基于模型的COBWEB算法、基于密度的DBSCAN算法、基于网格的STING算法 [2] 。k-means属于划分聚类算法，Wang [3] 等人通过引入蝙蝠算法(Bat)和模拟退火算法来改进k-means算法；Alsayat [4] 等人将遗传算法和簇间距离(OCD)引入到k-means算法中，优化和实现了社会媒体数据的实时聚类，准确地区分了不同类型的用户；Meng [5] 等人提出了一种基于噪声数据滤波和新的相似性距离度量公式，提高了稳定性。
用户负荷聚类方面，李志勇等人 [6] 基于自组织映射神经网络对用户负荷数据进行聚类处理，可视化程度较高；Jungsuk Kwac [7] 提出了基于自适应K均值等算法对住宅用户负荷进行聚类的方法；G Chicco [8] 等人基于蚁群和支持向量机算法提出了改进的用户负荷聚类算法；Albert等人 [9] 首先建立回归模型，然后使用HMM计算一系列参数，然后通过谱聚类方法对用户负荷进行聚类分析处理。
2. 负荷聚类基础理论
2.1. 聚类分析理论
2.1.1. 定义和过程
聚类分析，是将N个数据对象集合按照某种相似度规则划分为K个子集的过程，同时保证同一个子集中数据对象相似，不同子集中数据对象相异。聚类算法的数学表述形式为：若给定样本数据集合为A，集合B定义为A的一个非空子集，即：
(2-1)
(2-2)
(2-3)
聚类实现的过程主要是探索性地挖掘有价值的数据间内在联系。
2.1.2. 性能要求
聚类算法也许是数据挖掘中“新算法”出现最多、最快的领域，拥有如下典型要求：
1) 可伸缩性。
2) 处理多样化属性值。
3) 可以发现任何簇。
4) 输入参数的限制。
5) 抗噪能力。
6) 处理高维数据的能力。
7) 聚类评价。
2.1.3. 常见聚类算法
总的来说，聚类算法分为五类：层次方法、划分方法、网络方法、密度方法、模型方法，如下图1所示。
2.2. 两种聚类算法
2.2.1. k-means算法
k-means [10] 是一种无监督式学习算法，它是将M个数据集合按照某种特征划分为N个子集的过程。其基本原理如下：首先通过经典的统计学分析方法选取合适的聚类数目K；然后随机地选取K个初始值聚类中心，计算所有数据对象和K个聚类中心的距离，将其划分到就近的类中；接下来分别各个类中所
有数据点的平均值作为新的聚类中心，通过迭代的运算方式，重复计算数据点到聚类中心的距离；最后直到聚类中心不再改变或者准则函数收敛到某一个确定的值，算法迭代结束。k-means算法流程如图2所示。
k-means算法的优点包括适合发现球状簇，聚类准确高，运行时间快。
2.2.2. DBSCAN算法
DBSCAN [11] 是一种基于密度的聚类算法，是通过观察点的密度来识别不同的类别。一般在密度点比较高的区域会存在一个簇，而在低密度的区域也表示了噪声数据或者数据的离群值，它可以在高密度集群和噪声的数据库中发现任意形状的簇。DBSCAN总共需要两个参数：一个是邻域半径Eps，一个是MinPts，邻域半径的选择决定了聚类结果的好坏，如果邻域设置太大，会将异常值归到类别中，如果邻域设置太小，会将同一个类中的数据对象划分到别的类中。而同样MinPts如果选择太大，会导致样本点比较少的类消失，如果选择太小，就会导致一个类被划分到别的类中。其相关定义如下：
1) 邻域e：给定对象半径e内的区域称为该对象的e邻域。
2) 核心对象：假如给定对象e邻域内的样本点数大于等于MinPts，则称该对象为核心对象。
3) 直接密度可达：给定对象集合D，如果p在q的e邻域内，且q是一个核心对象，则规定对象p从对象q出发是直接密度可达的。
4) 密度可达：对于样本集合D，假如存在对象链
，则
是从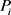
关于e和MinPts直接密度可达，则可以得出对象p是从对象q关于e和MinPts密度可达的。
DBSCAN算法对异常值不敏感，可以发现任意形状的簇，还可以识别出异常噪声点。但是需要设置邻域半径e和MinPts两个参数，其主要的缺点有如下几个方面：
1) 时间复杂度。DBSCAN的时间复杂度高，在面对高维数据集时显得异常困难。
2) 邻域半径Eps和MinPts的选取。对于在一个类中的所有点，这些点的第k个最近邻大概距离是相同的，所以要保证噪声点的第k个最近邻的距离较远，然后依据每个点和它的第k个最近邻之间的距离来选定。
3) 当空间聚类的密度不均匀时，聚类质量较差。某些簇内距离很小，相反某些些簇内距离很大，但Eps是可以确定的，那么大的点可能被误判为边界点或离群点，如果Eps过大，会导致小距离的簇内含有一部分便捷点或离群点。
2.2.3. 两种算法比较
综上所述，表1比较了本章中两种不同的聚类算法的性能。
3. 用户负荷聚类分析
3.1. 数据相关说明
3.1.1. 数据来源
本文研究的用户负荷数据取自SCADA系统数据库，数据主要包括某地区供电公司及其下属县区用户的电压，电流以及有功，无功等测量值，采样频率为15分钟一次，10 kV为对象用户主要电压等级，其中还包括少量较高电压等级，比如35 kV、20 kV、220 kV、110 kV等，负荷记录数大约77,312条，具体信息如下表2所示。
3.1.2. 数据预处理
1) 异常数据修正
样本数据总是会存在一部分异常数据，这里需要筛选掉。研究对象用户中存在少量用户有功负荷为负值，判定可能会发电用户，以及确实负荷数据量比较大的用户直接过移除，经过滤后，用户负荷数量总计77,656条，即总样本数。以下给出负荷变化率曲线作为判据，来判断所研究用户负荷曲线中突升，突降等数据。
(3-1)
通过上式可知用户负荷在d点的变化率序列为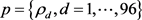
,当这个值超过预先设定的阈值则将其看作异常数据。
Table 1. Summary and comparison of clustering algorithm performance
表1. 部分聚类算法性能总结与比较
Table 2. User voltage level distribution
表2. 用户电压等级分布情况
2) 数据归一化处理
当我们在对负荷进行聚类分析时，相似性是需要考虑的主要方面，在这里采取最大值归一化处理，去掉负荷曲线的基础部分，凸显曲线之间的走势相似性。公式如下：
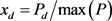(3-2)
进行归一化处理后，预处理环节到此结束。
3.2. 经典聚类算法对比
如表3所示，我们选取四类聚类算法展开分析：基于模型(EM,SOM)，基于层次(Single,Ward)，基于密度(DBSCAN,OPTICS)以及基于划分(k-means,FCM)。
3.2.1. 有效性评价指标
在接下来的工作中，我们采用k-means算法对所要研究的用户负荷数据进行聚类分析，引入SSE,DBI,CHI三种有效性指标对聚类结果进行评价。观察图3可知，CHI指标最佳聚类数为2，因此类别数太少不利于研究。
观察图4及图5，SSE和DBI指标曲线找到的最佳聚类数虽然是相同的，但DBI曲线的极值位置更容易判定，因此更有利于简化计算，所以在本人文的研究中可以将DBI作为聚类分析的有效性评价指标。
Table 3. Various types of classical clustering algorithms
表3. 各种类型的经典聚类算法
3.2.2. 常用算法对比
本章实验部分采取五种聚类分析方法进行分析，从用户负荷样本数据中选取1到14 K条数据进行分析，然后对比分析这五类算法所需的实际运行时间。如图6所示，k-means和FCM计算时间都较短，切曲线平稳，收数据集规模影响很小，对比前两种算法，Single算法所需时间较长，且所需运行时间随数据集规模的增长而大幅增长，结果不尽人意。继续观察图7，DBSCAN和EM算法所需时间非常长，并且曲线不平稳，随着数据集规模的增长所需运行时间也大幅增长。综合考虑之后，k-means和FCM两种算法表现都较为不错，因此在本文的实验部分主要采用k-means算法来对用户负荷样本数据进行聚类分析。
3.3. 样本数据降维
当对低维数据进行聚类分析是，由于低维数据完整性好，噪声小等优点，我们应用聚类算法处理上
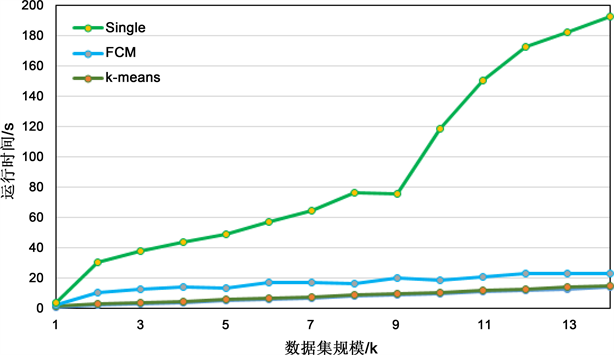
Figure 6. Single, FCM, k-means three algorithms run time required
图6. Single, FCM, k-means三种算法运行所需时间
Figure 7. DBSCAN and EM two algorithms run time required
图7. DBSCAN和EM算法运行所需时间
述数据是可以方便得出各种数据点的相似度，依次实验结果更加精确。这里采用主成分分析法PCA对样本数据进行降维处理，所得结果累计方差图如图8所示。
从图中结果可观察到原始样本数据集主要存在于前四个主成分中，所以考虑到降维的目标，便于算法的计算和运行，我们选择前四个主成分来进行研究，从而实现了降维的目的。
3.4. 聚类结果分析
3.4.1. 聚类结果
针对降维后的用户负荷样本数据，本实验采用k-means进行聚类分析，为了达到全局最优解，本实验重复进行二十次聚类分析，其中DBI指标为有效性评价指标，即DBI最小时即为所得的聚类结果。图9为进行聚类分析后的各聚类中心点。
由数据结果可知，经过聚类分析后用户负荷数据被划主要划分为五类，包括：晚高峰型用户，双峰
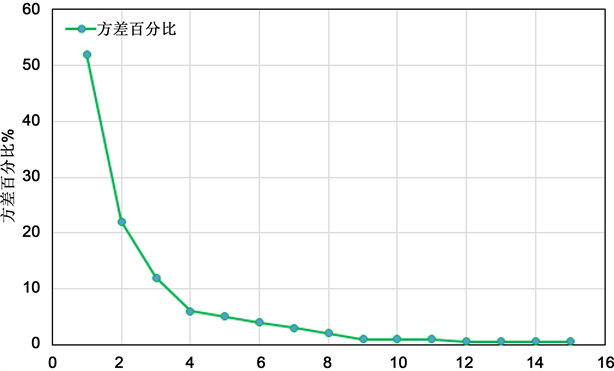
Figure 8. The dimensionless accumulation variogram
图8. 降维累计方差图
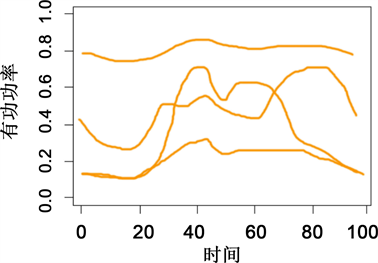
Figure 9. User load curve clustering center diagram
图9. 用户负荷曲线聚类中心示意图
型用户，单峰型用户，平稳型用户以及避峰型用户。由于第五类避峰型用户组只占了百分之三左右，因此就不在上图曲线中表示出来了。具体用户数和占比如表4。
3.4.2. 用户负荷构成及用电行为分析
依据相关规定我们将所得用户负荷数据中的用户大概划分为十五类，如表5所示。
本节将依据上节的聚类结果，以下选取三种曲线来进行研究，深度分析用户属性：
1) 晚高峰型用户
晚高峰型用户即为普遍型用电用户，用户的用电负荷变化曲线负荷负荷通常的日负荷变化曲线。即从早上五点开始，负荷开始上升，截止到中午十二点左右，负荷开始下降，下降原因可能为用户午休之类的行为。从下午四五点开始，用电负荷开始攀升，上升原因归结为用户下班回家等行为，到家中之后的日常活动会导致到晚八点左右的用电负荷达到顶峰状态。之后的时间段伴随着用户的睡眠等行为用电负荷开始下降。
晚高峰型用户数占总用户数量的约52%，是五类用户中占比最大的一类。其聚类中心图及包络图如图10及图11所示。
Table 4. The number and proportion of users in each category
表4. 每个分类中用户数量及占比
Table 5. Users of different power users in each category
表5. 每类中不同用电属性用户构成
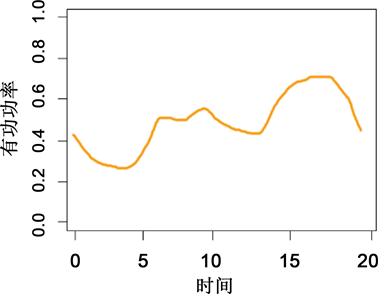
Figure 10. Late peak user center load curve
图10. 晚高峰型用户中心负荷曲线
Figure 11. Late peak user clustering center envelope
图11. 晚高峰型用户聚类中心包络图
从以上统计结果可以看出，从属性构成上来讲，晚高峰型用户以公变用户为主，公变用户数量为33,662个，所占比例高达84%，由此我们可以得出公变用户的用电模式即为晚高峰型，同时也几近于实际生活中一般居民的用电行为模式。在这晚高峰型用户属性中，同时包含有居民用电用户，非工业用户和一小部分工业用户。从以上分析可以看出晚高峰型用户组的构成还是较为复杂的，从海量的用户负荷数据聚类分析结果来看，即使是不同行业的用户，用电习惯也是趋于一致的，因此这些不同行业的用户可以划分到同一类型用户组中。
2) 单峰型用户
单峰型用户用户数量基本保持一致。在单峰型用户中，观察可知，曲线存在一个用电高峰，从整体变化趋势上看，负荷高峰和低估用电负荷差别并不大。单峰型用户数占总用户数约17%，其聚类中心图及包络图如图12及图13所示。
Figure 13. Unimodal user clustering center envelope
图13. 单峰型用户聚类中心包络图
从以上统计结果可以看出，从属性构成上来讲，在单峰型用户中，普通工业用户约占30%，公变用户约占29%，非工业用户约占19%，大工业用户约占6%，居民用户约占3%，农业用户约占5%，同时还包含一小部分用点属性不明的用户。上图中观察可知，单峰型用户用电高峰的时间段类似于双峰型用户的第一个高峰时间段，且从变化趋势上来看，整体变化较为平稳，高峰和低谷用电负荷相差不大，从用户结构上来看，这类用户是以普通工业用户为主，因此白天的用电负荷没有很高。
3) 平稳型用户
平稳型用户即为我们要研究的第四类用电用户，平稳型用户的数量为9217，占总用户数约12%，它的负荷曲线相较其他四种有明显区别。该类型用户负荷曲线整体变化趋势平缓，而且一天内的负荷变化较小，所以称作平稳型用户。从实际来看，该类型用户的负荷变化较为复杂，单整体变化趋势很平稳，其有功标幺值处于0.6~0.8数值区间，说明该类型的用电负荷有功功率水平相当高。其聚类中心图及包络图如图14及图15所示。
从以上统计结果可以看出，从属性构成上来讲，大工业用户约占28%，公变用户约占26%，非工业用户约占14%，商业用户约占13%，农业用户约占3%。分析可知该类型用电用户的主要构成是大工业用户和公变用户，而从一般来讲，大工业用户的生产都是全天不间歇运转，因此负荷水平很高。
3.5. 小结
本章首先是对实验样本数据的说明，包括数据的来源和预处理过程；接着从效率和准确度方面对几种经典聚类算法进行对比分析；然后是对用户高维负荷数据进行降维的论述；本节最后是对聚类结果的分析，首先阐明了聚类结果，然后通过聚类结果对用户负荷的构成和用电行为进行了分析和论述，体现了聚类分析对把握用户用电规律，优化电网运行的重要性。
4. 结论
本文的研究对象为某一地区的用户用电负荷数据，通过对样本数据进行聚类分析等初步研究，证明了所提方法的可行性和有效性。不过在聚类算法的研究和应用拓展方面仍然有较大的提升空间，总结为以下三点：
1) 在当今信息化和智能化时代，数据无时无刻都在产生，当我们面临海量数据进行进行聚类分析时，使用的主流工具依然是Hadoop等大数据平台，而没有从聚类算法本身进行改进和推广，比如在聚类分析
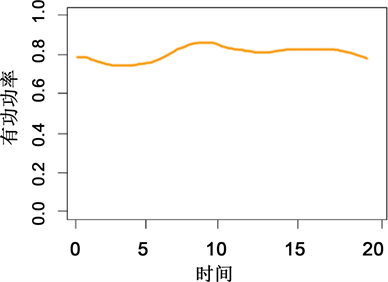
Figure 14. Stationary user center load curve
图14. 平稳型用户中心负荷曲线
Figure 15. Stationary user clustering center envelope
图15. 平稳型用户聚类中心包络图
之前对样本数据的预处理以及降维处理，都是非常重要的，所以我们需要进一步的研究相关的数据挖掘算法以及聚类方法，以缩短运行时间，提高计算效率以及准确度。
2) 在用户电力负荷研究方面，应用聚类分析方法对电力用户的构成进行分析，但是负荷建模以及负荷预测等方面的精确度还有待提升。
3) 负荷聚类算法的改进方面，本质上来讲，聚类算法是一个优化的过程，聚类算法求解的过程是经过多次迭代，所以其全局收敛性不能得到精确的把握；一些算法可能取得的聚类效果较好，但是所需参数会过多，计算时间过长，从而拉低了运算效率，面对实际问题时可用价值不高。
致谢
本工作得到河南省杰出青年项目(No. 164100510017)、973项目(No. 613237)的支持，感谢吴青娥教授在实验和语言方面给予的帮助，感谢评阅论文的各位专家。
NOTES
*通讯作者。