基于矩阵优化填充和结构性先验统计信息的气象数据恢复

Meteorological Data Restoration Based on Matrix Completion and Prior Features

摘要: 由于观测手段和观测背景的限制，再加上环境复杂，很多时候只有部分气象观测资料可用，为了在这种背景下进行气象预报，充分完备的气象资料是重要基础，因此基于零散的部分观测数据、先验数据的统计特征和矩阵优化填充技术的气象资料恢复研究具有重要的工程价值和数学意义，其研究在国内外尚属空白。本文旨在通过部分观测资料，充分利用矩阵的低秩性和气象观测数据的内在结构性先验统计信息，应用矩阵填充的奇异值阈值化SVT算法，优化分析得到欠缺数据，从而获得填充的补全数据。实验结果表明，基于结构性先验信息和矩阵优化填充方法得到的数据准确率明显取决于矩阵格式选择和气象数据本身特性，而且本文通过理论和实验分析出最佳的矩阵优化填充模型，表明当可利用的资料占比高于临界采样率时，数据填充误差可控制在10%以内，可以有效地解决预报和分析时的观测资料数据缺失不全的问题。

Abstract: Because of the limitation of observation means and background, combined with the complex environment, only some observation data are available. For the sake of better weather forecast, the research of meteorological data restoration based on part of observation data and matrix completion would have important scientific significance. This paper aims to, through part of real-time observation data, according to the low rank of a matrix, with applying SVT (Singular Value Thresholding) algorithm of matrix completion, obtain the deficient data so that one can make weather forecast better. The experimental result shows that the accuracy of forecast with matrix completion method is obviously higher than that with classical statistical method. When available data proportion is higher than the critical sampling proportion, errors of data filling can be controlled within 10%, which meet the requirements of meteorological data.

1. 引言

气象信息数据的获取是进行气象预报的前提，由于观测手段和观测背景的限制，再加上环境复杂，很多时候只有部分气象观测资料可用(可以获取)，为了在这种背景下进行气象预报，充分完备的气象资料是重要基础，因此基于部分观测数据和矩阵填充的气象资料恢复研究具有重要的科学意义 [1] 。本文旨在通过部分观测资料，根据矩阵的低秩性和气象观测数据的内在结构性先验信息，应用矩阵填充的SVT算法，得到欠缺的数据，从而获得补全数据。

近几年来，在工程控制、机器学习和计算机视觉等应用科学的众多领域，人们越来越感兴趣于如何利用非常有限的信息恢复出满足某种条件的未知信号 [2] ，这就涉及到如何对稀疏信号进行有效编码的问题 [3] 。例如，文献 [4] 提出的压缩感知(compressed sensing，CS)理论即通过少数的随机测量值完全或近似恢复出未知信号。与压缩感知理论相类似，矩阵填充(matrix completion，MC)理论也是通过对未知信号进行有效的降维处理，然后求解相关的稀疏信号重构问题，即通过少量的稀疏采样值完全或近似恢复出原始信号。矩阵填充的一个典型例子是Netflix问题 [5] ，该公司让用户在观看影碟后对电影打分，然后该公司根据用户对于影片的打分数据对用户喜好进行预测，设计新的预测方法。矩阵填充理论已被广泛的运用到量子理论、人脸识别、在线推荐系统等很多实际问题中，当然也包括气象领域的问题。比如，对于海上航行的船舶，由于观测手段和观测背景的限制，再加上环境复杂，通信往往出现断断续续甚至中断的情况，只有部分随船观测资料和历史背景资料可用，为了在这种背景下进行水文气象预报保障服务，基于部分观测数据和矩阵填充的天气预报的研究具有重要的科学意义和军事意义。还有，对于无人值守的海岛气象自动观测站，由于系统可靠性等原因，观测数据丢失是会经常发生的，面对该问题，目前除临近插值(或同化)外，别无它法。

同时，研究经验表明，气象数据具有很强的结构性和周期性(先验特征信息) [1] [6] ，在矩阵格式下就表现为低秩性，本文将结合气象数据矩阵的低秩性，应用矩阵填充技术SVT进行缺失数据的补全。

2. 矩阵填充

一个矩阵如果只观测到了它的一部分元素(这一部分元素可能占该矩阵元素很低的比例)，我们要推测出它的其他没有观测到的元素的信息，这便是矩阵填充所研究的问题。如果对于矩阵没有任何条件限制，矩阵填充问题的解将是无穷多的，是不可解的 [5] [7] ，但是在实际问题中，很多时候我们遇到的矩阵都是低秩矩阵或者渐进低秩矩阵，比如本文利用到的历史资料矩阵便是低秩矩阵，对于低秩矩阵，研究表明，可以通过合适的方法准确恢复出原来的矩阵。矩阵填充问题总结起来就是求解核范数最小化问题 [7] 。虽然现在求解核范数最小化问题已经有了一些成熟的算法，但是目前这些算法的复杂度都很高，处理高维矩阵的填充问题会花费大量时间，也正因此，快速高效的矩阵填充算法也是矩阵填充问题的一个研究热点。目前已经诞生出很多快速高效的矩阵填充算法 [8] - [14] ，最早的是由Cai等人提出的SVT算法 [8] ，该算法受到压缩感知中Bregman迭代算法的启发，算法在迭代过程中对矩阵进行了奇异值分解，然后将较小的奇异值设置为0，生成新的矩阵进行反复迭代，此算法运行速度很快，对于高维低秩矩阵的回填效果很好。另外还有Ma等人提出的FPCA算法 [9] ，该算法也用到了矩阵的奇异值分解，并且在算法迭代过程中进行不动点连续处理。该算法不仅对于低秩矩阵的恢复效果很好，对于秩适中的矩阵也有较好的恢复效果。在这之后，又陆续出现了很多关于矩阵填充的快速高效算法。目前矩阵填充问题与算法的研究已经取得了极大的进展，但是理论的不成熟导致仍然存在很多问题，例如一些实际问题中需要填充的低秩矩阵，其核范数是固定的，此时应用核范数最小化方法求解显然没有意义，对于这些问题，需要提出新的算法。另外，矩阵填充理论在各领域的应用也是一个重要的研究方向，特别是气象领域。由于Cai等人提出的SVT算法 [8] 是目前最为流行的算法，也是应用最为广泛的算法，本文将采用该算法进行气象数据的填充。SVT算法基本思路如下：

对于给定的矩阵X，矩阵部分数据已知，即下面优化问题即是矩阵填充的数学模型：

$\min {\Vert X\Vert }_{*},\text{s}.\text{t}.X_{i,j}=M_{i,j},\left(i,j\right)\in \Omega ,$ (1)

如果矩阵中数据采样对于给定的某个常数C满足 $m\ge C{n}^{6/5}r\log n$ ，上式就会以较高的概率( $1-n^{-3}$ )恢复出矩阵缺失元素。这里 ${\Vert X\Vert }_{*}$ 表示的是矩阵的核范数，即所有奇异值的和，r为矩阵的秩，n为矩阵行数和列数中的最小值，m为矩阵中已知数据个数。由于求解(1)较为困难，上式可以松弛成如下优化问题：

$\min rank\left(X\right),\text{s}.\text{t}.X_{i,j}=M_{i,j},\left(i,j\right)\in \Omega .$ (2)

进一步，Cai等人把限制条件进行了改进 [8] ，不是直接相等约束，而是投影(投影算子设为 $P_{\Omega }$ )后具有相同的数值(即改为投影约束)，即：

$\min rank\left(X\right),\text{s}.\text{t}.P_{\Omega }\left(X_{i,j}\right)=P_{\Omega }\left(M_{i,j}\right),\left(i,j\right)\in \Omega .$ (3)

因此，可以通过迭代优化计算方法(4)直到达到某个停止条件，获得最终的优化矩阵X：

$\{\begin{array}{l}{X}^k=shrink\left(Y^{k-1},\tau \right)\\ Y^k=Y^{k-1}+{\delta }_k{P}_{\Omega }\left(M-X^k\right)\end{array}$ ， (4)

其中， $Y^0=0$ ， $shrink\left(Y^{k-1},\tau \right)$ 为一个非线性软阈值函数，阈值为 $\tau$ ， ${\delta }_k$ 为k步相应的步长。这里使用了两个重要的特性：稀疏性和低秩性。矩阵在迭代的过程中一直保持着稀疏性，同时矩阵必须是低秩的，否则该方法将失效。

很显然，矩阵填充问题是一个非适定性的问题。一般而言，如果一个矩阵仅仅由少量的采样元素组成，那么完全重构出原矩阵几乎是不可能的，因为对矩阵未知元素的填充有无限种可能性。如果没有其他约束条件，矩阵填充重构出的矩阵将不是唯一的。但是如果我们事先知道原始矩阵数据满足一定的条件，那么矩阵填充将变得可行，这个关键的条件就是矩阵的低秩性 [10] 。

在实际的气象数据处理问题中，我们希望恢复的未知矩阵往往都是低秩的或近似低秩的。文献 [12] 证明了未知矩阵的低秩性或近似低秩性是矩阵填充重构出矩阵唯一性的前提，未知矩阵的低秩性或近似低秩性从根本上改变了矩阵填充问题的非适定性。该文还证明了通过解决一个简单的凸优化问题，就可以用极其少量已知的采样元素精确填充得到未知的低秩矩阵 [13] 。

本文主要利用的就是气象观测数据矩阵的低秩性或近似低秩性来填补构造矩阵。在实际情况中，由于观测条件和人为等因素，气象数据有时候会出现缺失(甚至缺失的比例较大)，面临很大程度的不完整性，而如何利用已有的部分观测数据获取较为准确且结构性良好的整体数据，这便是本文要解决的问题。

3. 气象数据的先验特征

本文选取了大连海区2011年至2015年5年共计1825天完整历史天气数据，数据下载网站为http://tianqi.2345.com/wea_history/54662.htm。其中每一天的数据包括日期、最高气温、最低气温、天气类型、风向以及风力等5类数据。部分数据如表1，表中数据完整，数据量较大，作为本文研究的数据。另外，还可以利用经典统计方法对5年的数据进行相应的统计，获取经验性成果，提高天气形势反演的准确率并验证之。

Table 1. Historical Weather Data of Dalian (Part)

表1. 大连历史天气数据(部分)

3.1. 数据的规律统计特性

由于各物理量之间存在着明显的规律性，比如当时间为冬季的时候，最低气温将会接近其极小值，天气很可能会出现下雪天气；当风力为大风时基本不可能出现大雾天气等等。加之数据量较大，对数据进行统计得到的结果对于本文研究的先验特征具有重要支持依据。

由图1可以看出，自 2011 年 01 月 01 日 到 2015 年 04 月 14 日 ，大连海区共出现晴613天，多云466天，阴41天，雾36天，雨306天，雪86天，沙尘4天。其中最常见的天气是晴天，共出现613天，约占39.5%；沙尘天气最少，仅仅出现过4天，不足1.0%，在后续的数据处理上，由于其占比太低，故将沙尘天气略去；多云天气以及雨雪天气也较为常见，比例分别为30.0%、25.3%，阴、雾天气较少，比例约为2.6%、2.3%。

由图2可以看出，自 2011 年 01 月 01 日 到 2015 年 04 月 14 日 ，大连海区共出现北风390天，东北风142天，东风52天，东南风196天，南风249天，西南风191天，西风66天，西北风266天。大连海区主要以偏北风和偏南风为主，其中仅正北风和正南风而言，二者就占了约41.2%；而东风和西风相对而言出现的频率非常低，仅占约7.6%。这个规律性相当明显，在后续的数据填充中应当加以考虑。

由图3可以看出，自 2011 年 01 月 01 日 到 2015 年 04 月 14 日 ，大连海区共出现3-4级风5天，4-5级风913天，5~6级风525天，6~7级风104天，7~9级风5天。4~5级风是大连地区最常见的风，占了58.8%，频率在一半以上；5~6级风也比较常见，约占33.8%；4~5级风、5~6级风加起来共占92.7%，说明大连地区风的风力基本保持在4~6级左右，其他风力较为少见。由图4可以看出，自 2011 年 01 月 01 日 到 2015 年 04 月 14 日 ，大连海区共出现天最高气温−11~−6℃共21天，天最高气温−5~−1℃共151天，天最高气温0℃~5℃共281天，天最高气温6℃~10℃共168天，天最高气温11~15℃共163天，天最高气温16℃~20℃共183天，天最高气温21℃~25℃共295天，天最高气温26℃~32℃共290天。

由图5可以看出，自 2011 年 01 月 01 日 到 2015 年 04 月 14 日 ，大连海区共出现天最低气温−15℃~−11℃共24天，天最低气温−10℃~−6℃共174天，天最低气温−5℃~−1℃共247天，天最低气温0℃~5℃共237天，天最低气温6℃~10℃共172天，天最低气温11℃~15℃共211天，天最低气温16℃~20℃共288天，天最低气温21℃~25℃共199天。

由图6可以看出，自 2011 年 01 月 01 日 到 2015 年 04 月 14 日 ，大连海区共出现温差0℃~3℃共82天，温差4℃~7℃共1028天，温差8℃~11℃共420天，温差12℃~15℃共22天。大连地区一天的温差

Figure 1. The historical statistical weather class data of Dalian

图1. 大连历史天气现象统计

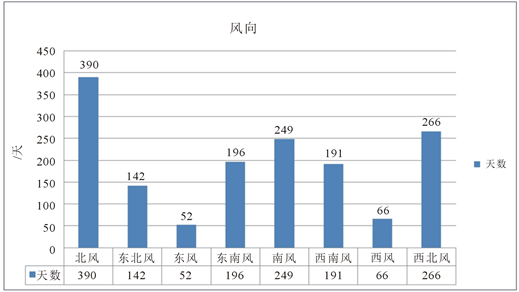
Figure 2. The historical statistical wind direction data of Dalian

图2. 大连历史风向数据统计

Figure 3. The historical statistical wind power data of Dalian

图3. 大连历史风力数据统计

Figure 4. The historical statistical highest temperature data of Dalian

图4. 大连历史最高气温资料统计

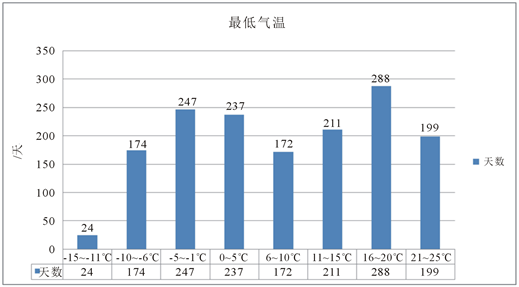
Figure 5. The historical statistical lowest temperature data of Dalian

图5. 大连历史最低气温资料统计

Figure 6. The historical statistical temperature difference data of Dalian

图6. 大连历史温差资料统计

主要在4℃~7℃左右，说明大连海区一天的温度变化并不大，这与大连海区的地理位置有很大的关系：大连地区靠海，海水的比热容比陆地的大，导致大连地区气温变化不剧烈。

正是上述数据的这种规律统计特性(图1~6)，可以说为数据缺失的填充恢复提供了物理基础。事实证明，这种数据的内在统计规律预示了矩阵内在的结构性和稀疏性，为数据填充可行性提供了依据。

3.2. 数据的分类

在日常生活中我们会发现，不同季节、不同天气的温差是不一样的，这说明温差与它们可能存在一定的关系，如果确实存在这样的关系，那么在矩阵中将会得到体现，即矩阵的低秩性特征。故在此将最高气温减去最低气温得到每日温差数据，以扩展我们的数据矩阵，得到更好的填充效果。经初步处理后部分数据如表2所示。

我们最终要将大连历史天气数据转化成矩阵来使用，而原始数据是由文本组成的，且种类繁多，这需要我们对原始数据进行分类，将相似的物理现象归为一类。下面我们就根据气象数据本身的特征进行分类。

Table 2. Historical weather data of Dalan (Part)

表2. 大连历史天气数据(部分)

1) 天气类型分类

由于大连海区这5年的数据中天气类型的种类十分复杂，共计123种，而人们日常关心更多的是恶劣天气，所以如果某天的天气类型没有变化，就取当日天气作为最终天气，例如2011年01月03号天气为晴，则最终天气类型便为晴天；如果某天的天气类型有所改变，则取恶劣天气做为当日天气类型，以此简化数据种类，例如 2011 年 04 月 18 日 天气为阵雨~晴，则取“阵雨”为当日分析天气。另外，为了进一步简化数据，削减数据种类，在处理数据时将含有雪的天气都归为一类“雪”，例如大雪、中雪、小雪最后都定为“雪”，按照此方法，最终天气类型被简化成6种基本天气类型，分别是雪、雨、雾、阴、多云、晴。

2) 风向分类

风向和天气一样，种类多样，比较复杂，共计64种。我们研究风矢量的时候和研究天气一样，更多的是关心大风的影响(而非常细化的风向考虑相对少一些)。故如果某日风向无变化则取该风向为当日风向；若风向改变，但风力不变，则取初始风向为当日风向；如果风向改变并且风力也改变，则取较大风力等级对应的风向作为当日风向。例如 2011 年 01 月 01 日 风向为北风，则当日风向为北风； 2011 年 01 月 02 日 风向为北风–西北风，风力4~5级未变，则取初始风向北风作为当日风向；而 2011 年 01 月 21 日 风向为东北风–北风，风力为6~7级~5~6级，则取较大风力6~7级对应风向东北风作为当日风向。最终风向简化成8类，分别是北风、东北风、东风、东南风、南风、西南风、西风、西北风。

3) 风力分类

日常生活中由于我们更多地关心大风的风力影响，所以对于风力的分类处理比较简单，如某日风力未变则该风力为当日风力；如果风力改变则取大风力为当日风力。例如 2011 年 01 月 19 日 风力为4~5级~5~6级，则当日风力为5~6级。

4)气温温差分类

将天最低气温、天最高气温和日气温差数据中的摄氏度符号“℃”直接去掉，然后作为其等级即可。经分类处理之后部分数据如表3所示。

3.3. 数据的结构性等级划分

经过上面的数据分类处理之后，我们在合理范围内将数据的种类降低，这对于后续的矩阵处理是非常有利的，而且因为我们更多是关心恶劣天气的影响，所以这对最终数绝填充结果影响并不大。现在

Table 3. Historical weather data after classification (Part)

表3. 经分类的大连历史天气数据(部分)

我们要将数据进行相应的编号，即结构性等级划分的数字化，得到新的数字矩阵。这样便可以将大连海区的历史数据转化成数据矩阵处理(表4~9)。

经数字化处理之后部分数据如表10所示(日期数据未处理)：

时间维对于整个大连海区历史天气数据矩阵而言是非常重要的一维，因为时间对应的一年四季，会出现哪样的天气现象是十分有规律性的，它包含着丰富的物理意义，与其它物理量的内在联系也非常明显，故在此将时间维分四类进行数字化处理，并在之后的处理中比较各类处理方法的优缺点。

1) 按月处理(表11)

1.1) 竖排结构

将5年1825天的数据排成1825 × 7的矩阵，顺序不变。

1.2) 横排结构

将5年1825天的数据排成365 × 35的矩阵，其中1~7列为2011年的数据，8~14列为2012年的数据，15~21列为2013年的数据，22~28列为2014年的数据，29~35列为2015年的数据。

2) 按季处理(表12)

2.1) 竖排结构

和按月处理竖排一样，将5年1825天的数据排成1825 × 7的矩阵，顺序不变。

2.2) 横排结构

同样，将5年1825天的数据排成365 × 35的矩阵，其中1~7列为2011年的数据，8~14列为2012年的数据，15~21列为2013年的数据，22~28列为2014年的数据，29~35列为2015年的数据。

经过将数据进行数字化处理，最终得到了按月处理(竖排)、按月处理(横排)、按季处理(竖排)、按季处理(横排)四种类型的数据。之所以这么做是因为不同结构的数据各物理量表现内在联系的方式不一样，所得到的矩阵的秩也是不一样的，运用这四种结构分别处理得到结果，再进行比较得到最优结构。

Table 4. Digitization of highest temperature

表4. 最高气温数字化

Table 5. Digitization of Lowest Temperature

表5. 最低气温数字化

Table 6. Digitization of Temperature Difference

表6. 温差数字化

Table 7. Digitization of Weather Class

表7. 天气类型数字化

Table 8. Digitization of Wind Direction

表8. 风向数字化

Table 9. Digitization of Wind Power

表9. 风力数字化

4. 基于部分数据和先验特征的气象数据填充

本文在研究前人的系列工作上，首先将已经数字化的大连历史天气数据输入到不同矩阵格式中(按季节、按月、竖排、横排等)，再利用矩阵填充的SVT算法对数据进行填充。为了测试算法的效能，我们利用不同的采样率随机采样以得到各采样率下的矩阵填充相对误差，比较得到多高的采样率下矩阵填充相对误差能控制在10.00%以内。运算结果如表13所示。

Table 10. Digitization of historical weather data of Dalian (Part)

表10. 经数字化的大连历史天气数据(部分)

Table 11. Processing the data according to months

表11. 按月处理数字化

Table 12. Processing the data according to seasons

表12. 按季处理数字化

在相对填充误差10%左右的范围在进一步细化采样率，得到相应的误差率，从而找出相对填充误差为10%对应的临界采样率，结果如下(表14)：

将表15中的数据细化(采取更小的步长)分别做成曲线图，如图7、图8所示。

由相对填充误差图可以看出，随着数据采样率的提高，误差在不断减小。其中当数据采样率在50%以下时，随着数据采样率的提高，误差在迅速减小；而当数据采样率在50%以上时，随着数据采样率的提高，误差减小的速率较慢。另外由图可以看出，无论数据是按月处理还是按季处理，横排结构的数据误差都要小于竖排结构的误差，即横排结构优于竖排结构；而观察按月处理或是按季处理，可以看出在正常范围内无论是横排结构还是竖排结构，数据按月处理的误差均小于按季处理的误差，即按月处理优于按季处理。所以最优数据结构为按月处理横排结构，此时数据填充的误差最小，天气数据填充的效果最好。要将误差控制在10.00%以内的的临界采样率如表16所示。

5. 按月横排矩阵格式最优化分析

根据SVT算法中矩阵低秩的特性，即对于同样的数据秩最低时SVT填充效果最佳，根据优化方程式(1)

Table 13. The error rate under different sampling rate

表13. 不同采样率下的误差率

Table 14. The error rate according to months

表14. 按月处理误差率

可知，如果矩阵中数据采样对于给定的某个常数C满足 $m\ge C{n}^{6/5}r\log n$ ，上式就会以较高的概率( $1-n^{-3}$ )恢复出矩阵缺失元素。所以我们不妨定义一个矩阵恢复测度 $\xi$ ：

Table 15. The error rate according to seasons

表15. 按季处理误差率

Table 16. The threshold sampling rate

表16. 临界采样率

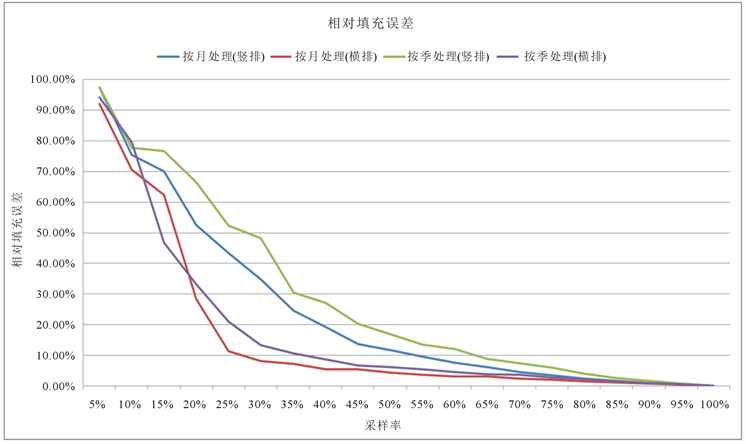
Figure 7. The error rate under different sampling rate

图7. 不同采样率下的误差率

$\xi \propto \frac{M}{m}\cdot \frac{r}{n}$ ， (5)

其中，r为矩阵的秩且满足 $r\le n$ ，n为矩阵行数和列数中的最小值，m为矩阵中已知数据个数，M为矩阵数据总个数即总行数和总列数的乘积。显然， $\xi$ 越小，表明矩阵越易于恢复填充，相反 $\xi$ 越大，表明

Figure 8. The error rate under different sampling rate (refined)

图8. 不同采样率下的误差率(细化)

矩阵越难于恢复填充。这一点很容易从直观上去解释，如果已知的数据个数m越大(其他参数固定)，显然矩阵需要填充的数据就越少，越容易填充，极限情况则是没有数据缺失 $m=M$ ，填充率可达100%。相反，如果 $m=0$ 即没有已知数据，则 $\xi \to +\infty$ 表示矩阵无法填充。另一方面，如果已知的数据个数m已定的情况下，矩阵的秩r越大， $\xi$ 越大，表明矩阵越难于恢复填充，如果 $r=n$ ，表示满秩，数据填充困难(如果有数据缺失的话)。相反，矩阵的秩r越小， $\xi$ 越小，表明矩阵越易于恢复填充，如果 $r=1$ ，且 $n\gg 1$ 时， $\xi \to 0$ ，表明矩阵数据中只有一行或列就可以表出其他行列数据。特殊情况，如果 $r=0$ ，表示矩阵为0矩阵，直接不必填充即可获得结果。

所以，我们只需证明按月横排数据时的矩阵具有最小的矩阵恢复测度 $\xi$ 即可。

假定有T年数据，每年固定数据量为p个，每个数据包含q个变量(比如日期，最高气温，最低气温，温差，天气，风向，风力等q个要素)，这些数据按照时间顺序写成矩阵形式则为

$X_{Tp\times q}=\left[\begin{array}{l}{x}_{1,1}{x}_{1,2}\cdots x_{1,q}\\ x_{2,1}{x}_{2,2}\cdots x_{2,q}\\ ⋮\\ x_{p,1}{x}_{p,2}\cdots x_{p,q}\\ ⋮\\ x_{Tp,1}{x}_{Tp,2}\cdots x_{Tp,q}\end{array}\right]$ , (6)

即为一个 $Tp\times q$ 的矩阵，不过是按照时间先后序列按照行进行排列。

那么，根据我们本文提出的四种模式：按月竖排处理、按月横排处理、按季竖排处理、按季横排处理四种类型的数据，不同的方式得到的矩阵分别为：

按月竖排：

$X_{mon,}{}_{Tp\times q}=X_{Tp\times q}$ , (7)

按月横排：

$X_{mon,}{}_{p\times Tq}=\left[\begin{array}{l}{x}_{1,1}{x}_{1,2}\cdots x_{1,q}{x}_{p+1,1}\cdots x_{(T-1)p+1,q}\\ x_{2,1}{x}_{2,2}\cdots x_{2,q}{x}_{p+2,1}\cdots x_{(T-1)p+2,q}\\ ⋮⋮\\ x_{p,1}{x}_{p,2}\cdots x_{p,q}{x}_{2p,1}\cdots x_{Tp,q}\end{array}\right]$ , (8)

按季竖排：

$X_{se,}{}_{Tp\times q}=X_{Tp\times q}$ , (9)

按季横排：

$X_{se,}{}_{p\times Tq}=X_{mon,}{}_{p\times Tq}$ . (10)

可见，按月竖排处理和按季竖排处理具有相同的矩阵结构形式，按月横排处理和按季横排处理也具有相同的矩阵结构形式。不同的是(见本文3.3部分)按月处理与按季处理时数据的分级不同。把数据(这里我们不仅采用大连地区多年的气象观测数据，同时我们测试了沈阳、青岛、北京等三个城市的多年数据)代入到不同的各自矩阵形式中，进行SVD(奇异值分解)分解得到如下结构(其他矩阵类似，省略)：

$X_{mon,}{}_{Tp\times q}=U_{mon,Tp\times Tp}\left[\begin{array}{l}{\sigma }_1\\ \ddots \\ {\sigma }_{r1}\end{array}\right]{V^{\prime }}_{mon,q\times q}^{}$ . (11)

在上述分解式(11)中取门限阈值(本文均取0.2)进行奇异值的阈值化处理，然后得到不同模式下的秩以及其他的参数，最终根据式(5)计算多个地方多年气象观测资料(沈阳、青岛、北京、大连四个城市历史资料)下的平均值，得到如下表结果(表17)：

所以，从理论分析及实验上来说按月处理(横排)对于气象数据矩阵的填充效果最佳。

6. 仿真试验

在前文中我们将大连海区历史天气数据分类、数字化，转化成矩阵变量，然后利用SVT矩阵填充算法对四种不同结构的数据在不同的采样率条件下依次进行了矩阵填充，当采样率在临界采样率以上时，填充效果是较为理想的，此时天气数据的相对填充误差控制在10%以内，这符合气象数据的误差要求。为了验证程序以及算法的适用性和填充准确度，我们选取最优数据结构按月处理(横排)来验证之。

Table 17. The comparison of restored measures (Average)

表17. 矩阵恢复测度比较(平均值)

目前我们是在已经掌握2011年至2015年大连海区所有数据的基础上，对数据进行随机采样来进行实验的，而在实际情况下，正是因为数据缺失，我们才会利用各种方法将数据补回来。因此，为了方便程序的适用性，我们进行了仿真检验试验，见图9、图10。

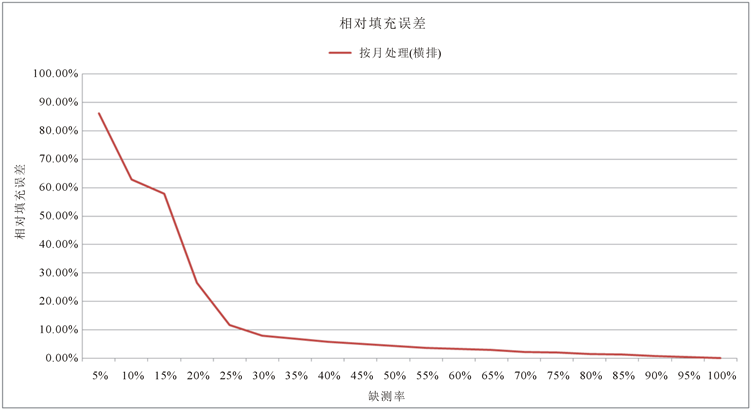
Figure 9. The error rate under different sampling rate

图9. 不同采样率下的误差率

Figure 10. The error rate under different sampling rate (refined)

图10. 不同采样率下的误差率(细化)

由图可以看出，临界缺测率约为72.10%，此时误差为9.81%。我们将缺测率72.10%对应到原始矩阵和填充矩阵。

7. 结论

本文利用大连海区2011年至2015年5年共计1825天的历史观测资料，对只有部分观测资料的情况下进行数据的恢复，并且运用历史资料进行了仿真检验试验，得到如下结论：本文模拟由于观测手段和观测背景的限制，再加上环境复杂，致使天气预报工作处于信息不全、数据缺少的状态，为缺失数据下的天气预报方法的研究提供了条件。本文所做的一部分探索是从气象数据的关联性出发，对其分类并进行数字化，实验结果表明，只要气象数据矩阵是低秩的，就可以从一小部分的关联性信息恢复得到整个的关联性信息，即一小部分关联性信息就能包含整个信息。从一系列的实验数据来看，如果有一部分相关度的气象数据，这一部分数据又是充分随机的，只要它们的数量能够达到一定的比例，即达到临界采样率，便可以通过它们恢复得到绝大部分缺失的气象数据。

利用大连海区历史资料对矩阵填充的SVT算法进行了仿真检验试验，结果表明：1)当缺测数据比例低于临界缺测率时，矩阵填充恢复的相对误差便可以控制在10%以内，这满足气象数据的使用要求，说明基于气象数据先验结构特性和矩阵优化填充技术对于气象数据补全具有很好的实用性；2)实验分析结果表明，大连地区气象观测资料月相关性明显强于季度相关性。

但是，本文在对数据处理方面仍有一定的改进空间，比如对数据的分类，文中为降低各项数据的种类，选择了“恶劣天气”、“大风”等这样的选择标准，致使某些真实情况有所弱化；另外，将类似的天气类型化为一类，比如将“小雨”和“暴雨”均改写为天气“雨”也会增大最终结果的误差。本文采用的历史数据只有大连海区等几个地区2011年至2015年5年的数据，我们都知道样本比例越高填充误差越小 [15] [16] [17] [18] ，所以扩充样本数量需要进一步探讨。

基金项目

国家自然科学基金(批准号：61471412，61771020，61273262)项目资助。

NOTES

^*通讯作者。