1. 引言
本文考虑如下非线性半定规划(NLSDP):
(1)
其中,函数
和
是连续可微函数,
表示所有
阶实对称矩阵构成的集合。“
”表示
为对称半负定矩阵。
非线性半定规划在工程设计、最优控制、金融风险等领域有着广泛的应用,见文 [1] - [6] 。序列二次规划(SQP)算法是求解传统非线性规划的有效算法之一,一些学者在非线性规划的SQP算法思想的基础上,提出了求解非线性半定规划的序列二次半定规划(SSDP)算法。Correa和Ramirez [7] 提出通过求解一个二次半定规划子问题产生搜索方向并将罚函数作为效益函数用于线搜索的SSDP方法。在一定的假设条件下,证明了算法的某些全局收敛性质。但该文没有分析产生搜索方向的子问题的相容性。
本文通过引进距离函数,提出一个新的SSDP算法,该算法具有如下特点:
· 产生搜索方向的子问题是相容的;
· 初始点任意,并且算法的线搜索保证效益函数的充分下降;
· 在一定条件下算法或收敛到问题的不可行稳定点,或收敛到问题的KKT点。
2. 算法
记
为所有
矩阵构成的集合,
为所有对称半正定(正定)矩阵构成的集合,
为所有对称半负定(负定)矩阵构成的集合。记NLSDP (0.1)的可行集为S。
定义1.1:对于任意矩阵
,
,定义A,B的内积为
其中
为矩阵的迹算子。
对于可微函数
,我们给出其微分为:
(1.1)
对于可微矩阵值函数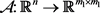 ,引入如下符号表示该函数在点x处的微分算子 [7] :
,引入如下符号表示该函数在点x处的微分算子 [7] :
其中
表示
关于
的偏导数。对于任意
,
定义为
(1.2)
若线性算子
定义为
,其中
,则伴随算子
为
NLSDP (0.1)的Lagrange函数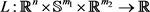 定义为
定义为
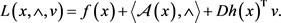 (1.3)
(1.3)
定义1.2 [7] :对于向量 ,若存在
,若存在 ,使得
,使得
 (1.4a)
(1.4a)
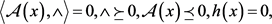 (1.4b)
(1.4b)
则称x为NLSDP (0.1)的一个KKT点,称 为相应的Lagrange乘子。
为相应的Lagrange乘子。
设 ,定义
,定义
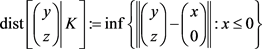
为 到集合K的距离,其中
到集合K的距离,其中 表示向量的欧式范数。
表示向量的欧式范数。
本文用于线搜索的效益函数定义如下:
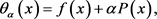 (1.5)
(1.5)
其中 由下式定义:
由下式定义:
 (1.6)
(1.6)
显然 当且仅当x为NLSDP (0.1)的可行点。
当且仅当x为NLSDP (0.1)的可行点。
下面给出求解NLSDP (0.1)的SSDP算法的具体步骤。
算法A
参数: ,
,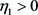 ,选取初始迭代点
,选取初始迭代点 和初始矩阵
和初始矩阵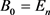 (单位阵)。令
(单位阵)。令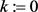 。
。
步骤1:求解如下二次半定规划子问题(简记为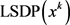 ),得最优解
),得最优解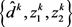
 (1.7)
(1.7)
其中 为m-阶单位阵。记
为m-阶单位阵。记
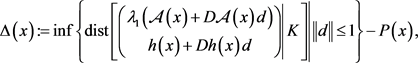 (1.8)
(1.8)
若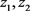 不全为0,且
不全为0,且 ,则算法终止,否则转步骤2;
,则算法终止,否则转步骤2;
步骤2:令 为如下二次半定规划子问题(简记为
为如下二次半定规划子问题(简记为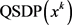 )的最优解:
)的最优解:
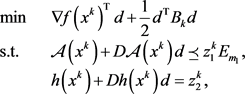 (1.9)
(1.9)
若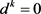 ,则算法停止;否则,转步骤3。
,则算法停止;否则,转步骤3。
步骤3:(更新罚参数)罚参数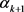 的更新方式如下:
的更新方式如下:
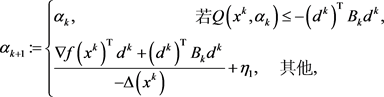 (1.10)
(1.10)
其中 。
。
步骤4:(计算步长)取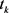 为
为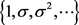 中满足如下式子的最大值:
中满足如下式子的最大值:
 (1.11)
(1.11)
步骤5:令 ,利用某种更新方式更新
,利用某种更新方式更新 为对称正定阵
为对称正定阵 ,返回步骤1。
,返回步骤1。
注2.1: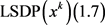 的最优解中的
的最优解中的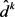 可能不唯一,我们将其构成的集合记
可能不唯一,我们将其构成的集合记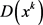 。
。
注2.2: 的KKT条件为
的KKT条件为
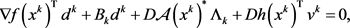 (1.2a)
(1.2a)
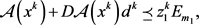 (1.12b)
(1.12b)
 (1.12c)
(1.12c)
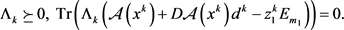 (1.12d)
(1.12d)
注2.3:步骤3的(1.10)能够保证罚参数的更新是单调不减的。事实上,若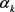 执行更新,则由
执行更新,则由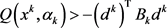 可得
可得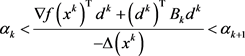 。
。
下面分析算法A的适定性,类似非线性半定规划的不可行稳定点的定义 [8] [9] ,首先给出非线性半定规划NLSDP (0.1)的不可行稳定点的定义。
定义1.3:设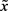 为NLSDP(0.1)的不可行点,若
为NLSDP(0.1)的不可行点,若
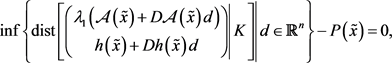
则称 为NLSDP (0.1)的不可行稳定点。
为NLSDP (0.1)的不可行稳定点。
本文需作如下基本假设:
A1:函数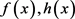 和
和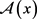 是连续可微的。
是连续可微的。
A2:存在正数a和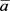 使得
使得

A3:由算法A产生的迭代点列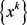 是有界的。
是有界的。
A4:对任意的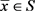 ,Mangasarian-Fromovitz约束规格(MFCQ)成立,即
,Mangasarian-Fromovitz约束规格(MFCQ)成立,即
1) 行满秩;
行满秩;
2) 存在非零向量 ,使得
,使得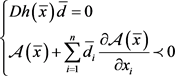
引理1.1:若假设1~3成立, 是由算法A产生的点列,
是由算法A产生的点列, 为
为 的最优解,则方向导数
的最优解,则方向导数 满足如下不等式:
满足如下不等式:
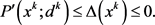
进一步的,若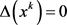 且
且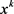 是NLSDP (0.1)的不可行点,则
是NLSDP (0.1)的不可行点,则 是NLSDP (0.1)的一个不可行稳定点。
是NLSDP (0.1)的一个不可行稳定点。
证明:设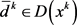 ,则
,则
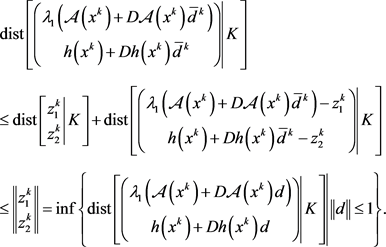
则由方向导数的定义及Taylor展式知
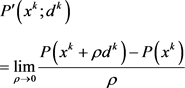


显然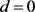 时,
时, ,因此结合(1.8)可得
,因此结合(1.8)可得 ,因此结合以上分析可知
,因此结合以上分析可知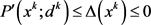 。
。
若 ,此时若
,此时若 为NLSDP (0.1)的不可行点,由不可行稳定点的定义知
为NLSDP (0.1)的不可行点,由不可行稳定点的定义知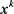 为NLSDP (0.1)的不可行稳定点。因此综合以上所述引理结论得证。,
为NLSDP (0.1)的不可行稳定点。因此综合以上所述引理结论得证。,
引理1.2:若假设1~3成立,算法有限步终止于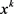 ,则
,则 或是NLSDP (0.1)的不可行稳定点,或是NLSDP (0.1)的一个KKT点。
或是NLSDP (0.1)的不可行稳定点,或是NLSDP (0.1)的一个KKT点。
证明:若算法终止于步骤1,则结合不可行稳定点的定义知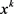 是NLSDP (0.1)的不可行稳定点。若算法终止于步骤2,则可知
是NLSDP (0.1)的不可行稳定点。若算法终止于步骤2,则可知 是
是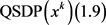 的最优解,将
的最优解,将 带入(1.12)可得
带入(1.12)可得
 (1.13a)
(1.13a)
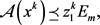 (1.13b)
(1.13b)
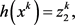 (1.13c)
(1.13c)
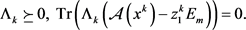 (1.13d)
(1.13d)
下面证明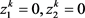 。(反证)若不成立,则
。(反证)若不成立,则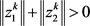 ,则可知
,则可知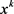 为不可行点。显然
为不可行点。显然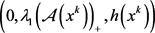 为
为 的可行解,因此
的可行解,因此
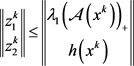 ,
,
其中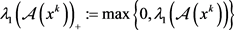 ,又因为算法在步骤1不终止,因此
,又因为算法在步骤1不终止,因此 ,因此可知
,因此可知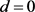 不是
不是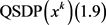 的可行解。矛盾。因此
的可行解。矛盾。因此 ,将
,将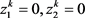 代入(1.13)可知
代入(1.13)可知 是NLSDP (0.1)的一个KKT点。
是NLSDP (0.1)的一个KKT点。
基于以上引理,若算法A在步骤1~2未终止,则结合更新公式(1.10)可知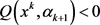 ,因此,线搜索(1.11)可执行,从而知算法A是适定的。,
,因此,线搜索(1.11)可执行,从而知算法A是适定的。,
3. 全局收敛性
基于引理1.2,本节中不妨假设算法A产生无限点列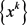 。接下来将证明
。接下来将证明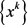 的聚点或是NLSDP (0.1)的不可行稳定点,或是NLSDP (0.1)的一个KKT点。
的聚点或是NLSDP (0.1)的不可行稳定点,或是NLSDP (0.1)的一个KKT点。
引理2.1:假设1~4成立,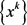 是由算法A产生的点列,若罚参数
是由算法A产生的点列,若罚参数 ,则
,则 为NLSDP(0.1)的一个不可行稳定点。
为NLSDP(0.1)的一个不可行稳定点。
证明:首先证明 是有界的。由
是有界的。由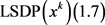 可知
可知 。显然
。显然 是
是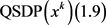 的可行解,因此我们可以得到
的可行解,因此我们可以得到

此外,由上式结合假设2,有

另一方面我们根据假设2,有
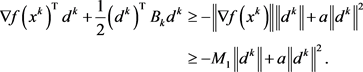
以上两式可以得到 是有界的。因
是有界的。因 ,则由罚参数更新公式(1.10)可知
,则由罚参数更新公式(1.10)可知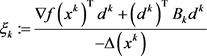 趋于
趋于 。而又结合
。而又结合 和
和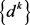 的有界性可知:
的有界性可知: 趋于0,若此式成立,则结合κ的定义及罚参数的更新方式可知
趋于0,若此式成立,则结合κ的定义及罚参数的更新方式可知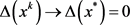 ,且
,且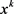 为不可行点。下面证明
为不可行点。下面证明 为不可行点。
为不可行点。
由(1.12a)可知
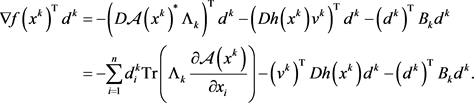 (2.1)
(2.1)
根据(1.12b)可知
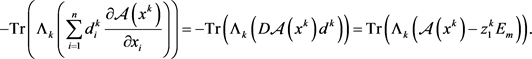 (2.2)
(2.2)
由(2.1),(2.2),结合(1.13c)可知
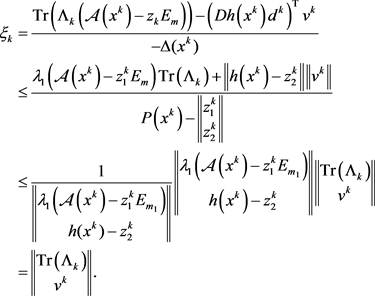
则结合罚参数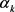 无界易得
无界易得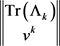 无界,因此
无界,因此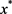 为不可行点(否则若
为不可行点(否则若 为NLSDP (0.1)的可行点,则由假设4,可知MFCQ在
为NLSDP (0.1)的可行点,则由假设4,可知MFCQ在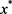 处成立。类似于文献 [10] 中定理5.1的证明,可知
处成立。类似于文献 [10] 中定理5.1的证明,可知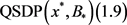 的KKT乘子集合
的KKT乘子集合 是非空且有界的。注意到
是非空且有界的。注意到 且
且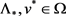 ,因此
,因此 是有界的)。再结合
是有界的)。再结合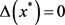 ,由定义即知
,由定义即知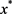 为NLSDP (0.1)的不可行稳定点。,
为NLSDP (0.1)的不可行稳定点。,
基于引理2.1,在下面的分析和讨论中不妨假设 ,结合罚参数的更新公式(1.10),可得如下结论成立:
,结合罚参数的更新公式(1.10),可得如下结论成立:
引理2.2:若假设1~4成立。则存在自然数 ,使得对任意的
,使得对任意的 ,都有
,都有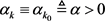 。基于引理2.2,在下面的分析中,不失一般性,假设
。基于引理2.2,在下面的分析中,不失一般性,假设
定理2.1:假设1~4成立, 为算法A产生的无限序列
为算法A产生的无限序列 的任意一个聚点,即
的任意一个聚点,即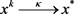 ,则
,则 或是NLSDP(0.1)的一个不可行稳定点,或是NLSDP (0.1)的一个KKT点。
或是NLSDP(0.1)的一个不可行稳定点,或是NLSDP (0.1)的一个KKT点。
证明:不失一般性,假设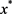 不是NLSDP (0.1)的不可行稳定点,下面将证明
不是NLSDP (0.1)的不可行稳定点,下面将证明 是NLSDP (0.1)的一个KKT点。首先证明若
是NLSDP (0.1)的一个KKT点。首先证明若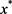 不是NLSDP (0.1)的不可行稳定点,则
不是NLSDP (0.1)的不可行稳定点,则
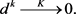
反证法,假设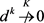 ,则存在常数
,则存在常数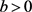 以及一个指标集
以及一个指标集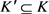 ,使得
,使得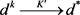 ,且
,且
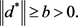 (2.3)
(2.3)
下面将证明分成两部分。
a) 证明存在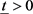 ,使得
,使得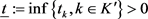 。
。
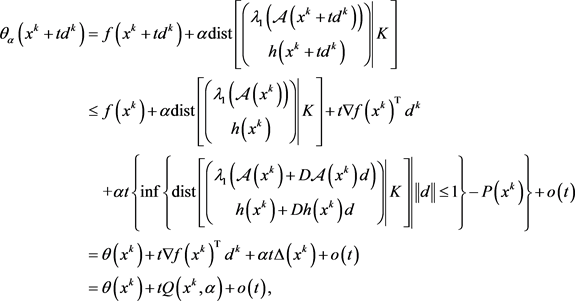
于是有
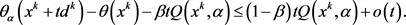
结合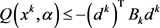 以及(2.3)可知
以及(2.3)可知 ,因此当
,因此当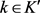 充分大时有
充分大时有
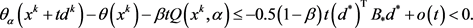 (2.4)
(2.4)
由此可知存在 ,使得
,使得 。
。
b) 基于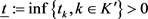 ,将导出矛盾。
,将导出矛盾。
由线搜索(1.11)可知 为非增序列。由
为非增序列。由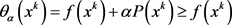 以及
以及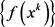 的有界性可知
的有界性可知 有下界。因此
有下界。因此 收敛。令
收敛。令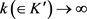 ,对(2.4)取极限得
,对(2.4)取极限得

显然矛盾。因此 。进而知
。进而知 。将
。将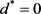 带入
带入 的KKT条件,得
的KKT条件,得
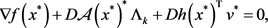 (2.5a)
(2.5a)
 (2.5b)
(2.5b)
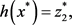 (2.5c)
(2.5c)
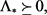 (2.5d)
(2.5d)
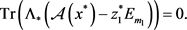 (2.5e)
(2.5e)
下证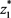 和
和 均为0。反证法,若不成立,易知
均为0。反证法,若不成立,易知 为不可行点,则
为不可行点,则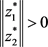 ,结合
,结合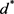 为
为 的一个可行解知
的一个可行解知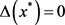 ,故
,故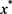 为不可行稳定点,矛盾。因此
为不可行稳定点,矛盾。因此 和
和 均为0。将
均为0。将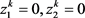 代入(2.5)即知
代入(2.5)即知 为NLSDP (0.1)的KKT点。,
为NLSDP (0.1)的KKT点。,
4. 结束语
本文提出了带有等式和半负定矩阵约束的非线性半定规划一个全局收敛的SSDP算法。基于非线性规划修正的序列二次规划算法思想构建两个半定规划子问题,通过求解子问题产生搜索方向,线搜索保证效益函数充分下降。在MFCQ等温和条件下,论证了算法的适定性和全局收敛性。
基金项目
获国家自然科学基金(No. 11561005),广西自然科学基金(No. 2016GXNSFAA380248)资助。
NOTES
*通讯作者。