1. 引言
在学校,孤僻学生不适应集体生活,不能和同学融洽相处,久而久之造成不好的心理,对学生自己和他人都有不利的影响,同时也会造成不良的学习表现。识别孤僻学生、关注学生心理健康,对高校管理者是必要的。孤僻学生在日常生活中的表现不同于其他学生,在就餐上表现为合群学生喜欢和同学一块吃饭,而孤僻学生则会较少和同学一起吃饭。分析学生就餐打卡数据,建立学生关系模型,从而找到孤僻学生。
国内对于学生间交往行为的研究较少,文献 [1] 中提到通过构建二分网络判断学生间的关系。鲁鸣鸣等人提出根据学生生活轨迹,建立简单的相遇模型,挖掘学生线下交往关系 [2] 。由于国内外大学生管理有较大差异,国外学生很少使用像一卡通这种设备,未见相关线下交往的研究成果。随着移动设备的世界化和位置服务的普及,人们使用移动设备产生了大量的位置信息数据,很多研究者利用这些位置信息分析人们的交往关系,这种基于位置信息的交往行为研究,与利用一卡通数据对学生进行交往行为的研究极为相似,从中可以得到启发。在2009年,Eagle N等人根据移动电话的位置信息预测人与人之间的关系,发现共现(同一时间在相同位置)是研究人与人间关系的重要指标 [3] 。Crandall D J等学者通过量化人与人之间的共现情况,建立概率模型,研究两人之间关系的紧密程度,提出了分辨两人是陌生人还是朋友的方法 [4] 。Xu Bin等人 [5] 通过分析室内定位数据,研究用户物理位置和社交之间的联系,提出了一个相遇时间、相遇频率与社交关系的模型,结果表明两人之间共现时长与其关系密切程度呈正相关关系。本文受到以上研究者所做工作的启发,利用学生使用校园一卡通就餐数据分析学生间关系时,也用到共现的概念,不过在这里共现是指两学生一块吃饭。根据学生共现次数、共现时间间隔建立学生间的关系模型,最后判断学生是否孤僻。
2. 学生就餐数据预处理
文中所用数据为2013级3680名学生第一学年的学生打卡数据,由学校网络中心提供,其中包括学生餐厅打卡、超市打卡、浴室打卡等信息,从中筛选餐厅打卡数据,共1,994,709条,数据格式如表1所示。
表1中第一列No为学生学号,为保护学生隐私,此学号由真实学号转换而成;第二列Date为打卡日期;第三列Time为打卡时间,为二十四小时制;第四列Pos为就餐打卡位置,包括一餐一楼、一餐二楼、二餐一楼等区域。
在一次就餐中,有的同学会在不同的窗口刷卡打饭,出现一次吃饭多次、不同时间打卡的现象。为解决此问题,把学生同一日期半小时内多次打卡视为一次打卡吃饭。处理后的数据如表2所示。表2中S-time表示一次就餐第一次刷卡时间,End time表示一次就餐最后一次刷卡时间。
3. 学生就餐数据分析
如果两名学生在同一时间出现在了同一地点,我们说这两名学生共现 [6] ,在本文中学生一起吃饭称之为共现。根据预处理后的学生吃饭时间,可以提取所有学生之间共现的次数和共现的时间间隔,并且研究这

Table 1. Sample of students’ dining data
表1. 学生就餐打卡数据样例

Table 2. Sample of students’ conversional dining data
表2. 学生的转换打卡数据样例
些特征和学生是否孤僻存在的联系;另一方面,人与人之间的关系会随着时间的推移而变化,只根据一学年的全部数据判断学生间的关系会有较大误差,所以把数据分成了上学期、下学期和一学年三个时间段。综合三个时间段内学生关系,可使结果更精确。
在平时校园生活中,大部分学生是使用校园卡买饭的,但是也有部分学生不在学校餐厅吃饭或很少在餐厅吃饭,这些学生的打卡吃饭信息太少,无法根据就餐数据判断学生是否孤僻,所以只选取了三个时间段内吃饭次数均多于15次的学生,共3587名学生。
下面分别对学生间共现次数、学生间共现时间间隔这些特征与学生是否孤僻做相关分析。
3.1. 学生间共现次数与学生是否孤僻之间的关系
学生在日常生活中,大部分学生是和朋友一块活动的,而孤僻学生则喜欢独来独往,在吃饭上表现为大部分学生会经常和其他的同学一块,而孤僻学生不会和其他学生一块吃饭,或是很少和其他同学一块。
根据2013级学生的就餐打卡数据,分别在上学期、下学期、一学年三个时间段对全部学生和孤僻学生做相关的统计。一名学生和学校其他所有学生都有共现概率,即每名学生和其他3586名学生都有共现信息,而一名学生不可能认识其他的3586名学生,只可能和少数的学生经常吃饭,所以在统计时使用了学生前五大共现次数的平均值。另外,由于仅了解到计算机系的哪些学生为孤僻的,所以,以下是对计算机系学生的统计。统计结果如图1~图3。
根据图1、图2、图3所示,上学期、下学期、一学年三个时间段做的学生共现次数的统计,均可以看出孤僻学生的共现次数较少,可以说共现次数与学生是否孤僻是有联系的,共现次数少的学生孤僻的概率较大。
学生在一时间段内打卡吃饭次数不同,学生间共现次数受学生打卡吃饭次数的影响,仅靠共现次数衡量他们的关系是不准确的。例如,在学年上学期,学生A打卡吃饭120次,和学生B一块吃饭40次,学生C打卡吃饭60次,和学生D一块吃饭40次,学生C和学生B的关系应该是要好于学生A

Figure 1. 2013 students’ times of co-occurrence for the first semester
图1. 2013级学生上学期共现次数分布图
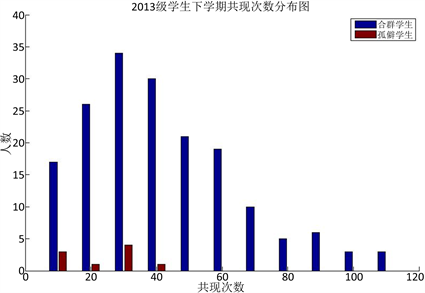
Figure 2. 2013 students’ times of co-occurrence for the second semester
图2. 2013级学生下学期共现次数分布图

Figure 3. 2013 students’ times of co-occurrence for the school year
图3. 2013级学生一学年共现次数分布图
和学生B的关系的。所以,用共现次数和学生吃饭次数的比值(共现指数)来表示学生间的关系是更加符合事实的。
对学校2013级计算机系学生在上学期、下学期、一学年三个时间段做共现指数的统计,在统计时使用了学生前五大共现指数的平均值。统计结果如图4~图6。
根据图4、图5和图6所示,上学期、下学期、一学年三个时间段做的学生共现指数的统计,均可以看出孤僻学生的共现指数较小,可以说共现指数与学生是否孤僻是有联系的,共现指数小的学生孤僻的概率较大。
3.2. 学生间共现时间间隔与学生是否孤僻之间的关系
在校园内,餐厅数量固定,上下课时间固定,很多学生在相近的时间、相同的餐厅打卡就餐,但实
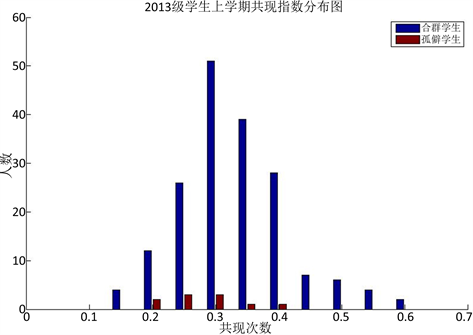
Figure 4. 2013 students’ exponent of co-occurrences for the first semester
图4. 2013级学生上学期共现指数分布图
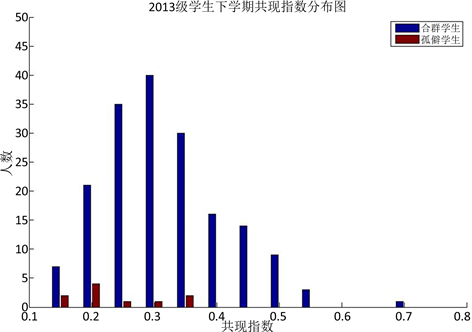
Figure 5. 2013 students’ exponent of co-occurrences for the second semester
图5. 2013级学生下学期共现指数分布图

Figure 6. 2013 students’ exponent of co-occurrences for the school year
图6. 2013级学生一学年共现指数分布图

Figure 7. 2013 students’ mean time interval for the first semester
图7. 2013级学生上学期平均时间间隔分布图
际中并没有交往关系,仅仅是偶遇。为减小此类现象对实验的影响,本文引入了平均时间间隔和最短时间间隔的概念。时间间隔是指两名学生两次共现的时间差。关系紧密的同学之间平均时间间隔和最小时间间隔会比较小,在一定程度上可以减小偶遇现象对实验结果的影响。
对学校2013级计算机系学生在上学期、下学期、一学年三个时间段做平均时间间隔的统计,在统计时使用了学生前十小平均时间间隔的平均值。统计结果如图7~图9。
根据图7、图8和图9所示,上学期、下学期、一学年三个时间段做的学生平均时间间隔的统计,均可以看出孤僻学生的平均时间间隔较大,特别是下学期的平均时间间隔分布图更加明显。可以说平均时间间隔与学生是否孤僻是有联系的,平均时间间隔大的学生孤僻的概率较大。
对学校2013级计算机系学生在上学期、下学期、一学年三个时间段做最小时间间隔的统计,在统计

Figure 8. 2013 students’ mean time interval for the second semester
图8. 2013级学生下学期平均时间间隔分布图
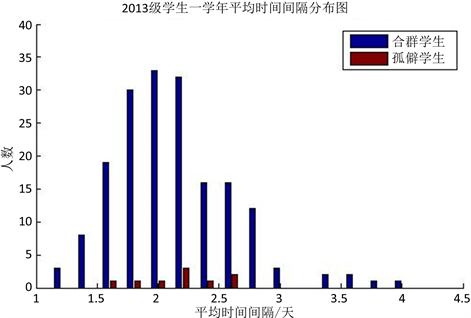
Figure 9. 2013 students’ mean time interval for the school year
图9. 2013级学生一学年平均时间间隔分布图
时使用了学生前十小的最小时间间隔的平均值。统计结果如图10~图12。
根据图10、图11、图12所示,上学期、下学期、一学年三个时间段做的学生最小时间间隔的统计,从上学期和下学期的统计分布图均可以看出孤僻学生的最小时间间隔较大,而一学年的统计分布图不那么明显。从实际出发,时间段越长学生间的最小时间间隔越小,最后固定在某一值,则一学年的统计分布图没有上、下学期的分布图明显是正常的。可以说最小时间间隔和学生是否孤僻是有联系的,最小时间间隔大的学生孤僻的概率较大。
4. 学生关系模型的建立与应用
4.1. 学生关系模型的建立
根据学生就餐打卡数据,判断哪些学生是孤僻的。根据学生共现次数、共现指数、平均时间间隔和最小时间间隔建立学生关系模型,量化学生间关系,计算学生间的关系值,以学生间的关系值评价学生

Figure 10. 2013 students’ minimum time interval for the first semester
图10. 2013级学生上学期最小时间间隔分布图
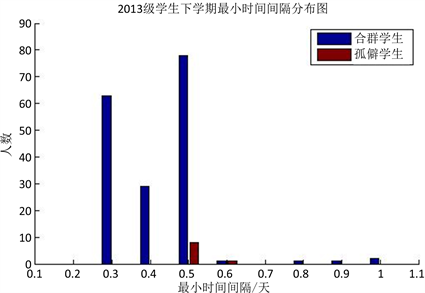
Figure 11. 2013 students’ minimum time interval for the second semester
图11. 2013级学生下学期最小时间间隔分布图

Figure 12. 2013 students’ minimum time interval for the school year
图12. 2013级学生一学年最小时间间隔分布图
间关系的紧密程度;以学生间关系值作为学生之间的距离,对3587名学生进行聚类,找出孤立点对应的学生,三个时间段内有两次或三次被表示为孤立点的学生定义为孤僻学生。
如果两名同学在同一地点、相邻时间打卡,则认为两名同学一块吃饭。在实际场景中,两名学生一起吃饭,3分钟内两人均可打完饭菜。两名同学在3分钟内且在同一地点刷卡视为共现。
学生间共现指数和共现次数在一定程度上表示了他们关系的紧密程度,值越大他们的关系越紧密,反之,关系越疏远。同时,在判断学生之间的关系上,平均时间间隔和最小时间间隔也起到一定的作用,值越小他们的关系越紧密,反之,关系越疏远。
为判断学生间的关系紧密程度,本文引入一种评价学生关系的模型:
(1)
其中
表示学生i和学生j一块吃饭的次数;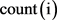 表示学生 的吃饭次数;
表示学生 对学生 的共现指数;
表示学生i和学生j一块吃饭的平均时间间隔;
表示学生i和学生j一块吃饭的最小时间间隔;关系指数
则表示学生i和学生j之间的关系,构成关系矩阵,
值越大则学生i和学生j的关系越紧密。
表示学生 的吃饭次数;
表示学生 对学生 的共现指数;
表示学生i和学生j一块吃饭的平均时间间隔;
表示学生i和学生j一块吃饭的最小时间间隔;关系指数
则表示学生i和学生j之间的关系,构成关系矩阵,
值越大则学生i和学生j的关系越紧密。
4.2. 层次聚类在学生关系模型上的应用
聚类是将样本分成多个相似对象集合的过程,是一种无监督的分类方法 [7] [8] 。其中层次聚类方法 [9] 是根据样本的簇间相似度进行合并或分解,直到满足某种或某些终止条件为止,最终把样本聚集成一些簇,簇内样本的相似度较大,簇间样本的相似度较小。根据关系矩阵 对学生进行层次聚类,寻找孤立点,找出孤僻学生。关系矩阵 中,值越大说明两人关系越紧密,即值越大对象之间的距离越小。
根据聚类原理不同,层次聚类可以分为凝聚层次聚类和分裂层次聚类。文中采用凝聚层次聚类算法,以学生为对象,每一名学生为一簇,以学生间的关系指数作为“距离”。本文使用了三种簇间距离方法,分别为最短距离、平均距离、最短距离和平均距离的结合,具体如下:
最短距离:簇间各对象间的最小距离,反应了簇间最要好的两名学生之间的关系紧密程度;
平均距离:簇间所有对象距离的平均值,反应了簇间所有学生之间的关系紧密度,并取均值;
最短距离和平均距离的和:最短距离和平均距离的和不仅联系了簇间关系最好的两名学生,而且反应了所有学生之间的关系情况;
根据上述三种距离方式对学生进行层次聚类,并对三种方法进行比较,找到一种较好的方法。
具体算法如下:
输入:包含n个对象的基本信息,终止条件簇的数目k。
输出:k个簇。
1) 将每个对象看作一个初始簇;
2) 根据距离度量标准找到最紧密的两个簇,合并,生成新的簇的集合,删除被合并之前的两个簇。
3) 重新计算新的簇和旧的簇之间的距离;
4) 重复2)、3)过程,直到簇的数目到k。
经过凝聚层次聚类,学生被分成了k个簇,每个簇包含一个或多个对象,簇内的学生关系比较紧密,簇间的学生关系较疏远,只有一个对象的簇是孤立的,从而找到孤立点对应的学生。实验中不断改变聚类的k值,根据不同k值下取得的结果确定最终的聚类数。分别在上学期、下学期和整学年三个时间段进行层次聚类,有两次或三次被表示为孤立点的学生定义为孤僻学生。
5. 实验结果
通过构建相遇模型和学生关系模型,利用层次聚类方法对学生进行聚类分析,最后发现孤僻学生。通过访问和性格评估的方式,对计算机系181名学生进行了是否孤僻的评估,获取了学生合群或孤僻的情况,其中有8名孤僻学生,其余为合群学生。以下是使用计算机系的学生进行实验验证,并做出结果分析。
以关系矩阵的值作为对象间的距离分别在上学期、下学期和整学年三个时间段进行层次聚类,分别使用了最短距离、平均距离、最短距离+平均距离三种距离方式,实验中不断改变聚类数k,最终选取效果较好时的距离方式和聚类数作为实验参数。三种距离方式和不同聚类数下所取得的结果如表3~表5。
总体精度为正确查找孤僻学生和合群学生的数量与学生总数量的比值,由于孤僻学生所占总学生的比例较小,仅用总体精度评估结果的好坏是不准确的,所以本文引入了查全率、查准率和F-Measure指标。孤僻学生的查全率为正确查找孤僻学生的数量与孤僻学生总数量的比值,孤僻学生的查准率为正确查找孤僻学生的数量与查找孤僻学生总数量的比值。F-Measure是综合了查准率和查全率的指标,孤僻学生的F-Measure指标如式(2)所示。

Table 3. The results summary table for the shortest distance
表3. 距离方式为最短距离时的结果汇总表

Table 4. The results summary table for the average distance
表4. 距离方式为平均距离时的结果汇总表

Table 5. The results summary table for the shortest distance + average distance
表5. 距离方式为最短距离+平均距离时的结果汇总表
(2)
其中F指孤僻学生的F-Measure指标值,P是孤僻学生的查准率,R是孤僻学生的查全率。查准率和查全率都可以表示模型结果的好坏,两者的值越大说明结果越好,F-Measure综合了查准率和查全率两者的值,F-Measure值越大,孤僻学生寻找得到的结果越好。
从表3~表5的对比可以发现距离方式为最短距离时得到的孤僻学生的查全率、查准率和F-Measure指标明显低于距离方式为平均距离和最短距离+平均距离所得的结果,最短距离的距离方式并不能得到较好的结果。从表4和表5的对比发现两种距离方式的总体精度和合群学生的查全率、查准率相差不大,孤僻学生的F-Measure、查全率、查准率有一定的差别,距离方式为平均距离的聚类数为900和950时F-Measure值较大,所得结果较好,距离方式为最短距离+平均距离的聚类数为880时F-Measure值较大,所得结果较好。距离方式为最短距离+平均距离时,随着聚类数的改变,F-Measure值变化较小,距离方式为平均距离时,随着聚类数的改变,F-Measure值变化较大。在孤僻学生寻找中,最短距离的距离方式所取得的效果较差,其他两种距离方式各有优势。
6. 结束语
利用就餐打卡数据分析学生间的关系,首先对原始数据做相关的预处理,把学生同一日期半小时内多次打卡视为一次打卡吃饭,把学生打卡时间转化成学生吃饭时间,对学生吃饭数据进行分析,建立相遇模型,并提取了相关特征,发现学生之间的共现次数和共现时间间隔与学生是否孤僻是有较大联系的。根据提取到特征的特性建立学生关系模型,量化学生间关系,计算学生间关系矩阵,以关系矩阵值作为对象间的距离进行凝聚层次聚类,寻找孤立点,找到对应的孤僻学生。在层次聚类中使用了三种距离方式,分别为最短距离、平均距离和最短距离 + 平均距离,其中最短距离的方式所取得的效果较差,其他两种距离方式各有优势。预测孤僻学生的查准率为66.67%,查全率为75%,证明建立的学生关系模型对于孤僻学生发现是有效的。