1. 引言
生物识别是一门基于个体的身体或行为特征建立起人类身份的科学,如指纹、脸、虹膜、声音、步态和签名识别等 [1] 。从智能手机到边境安全等多种身份管理和访问控制系统中,均需利用生物特征识别系统,这表明了利用生物特征识别技术进行人类识别的潜力,尤其是虹膜识别系统。
在虹膜识别算法中,最经典的归一化方法是Daugman提出的橡胶板模型 [2] ,除此之外,Wyatt等 [3] 提出的虹膜磨损最小的网状结构模型和Yuan等 [4] 提出的线性与非线性结合的归一化模型,以及Thornton等 [5] 提出的虹膜图像变形模式匹配的贝叶斯方法等,都有很好的识别性能。本文在Clark等 [6] 提出的虹膜动力学的理论模型的基础上,提出了一种结合房水折射和瞳孔扩张、收缩的弹性运动不对等性模型,对虹膜特征点位置进行偏差校正,此模型改善了房水折射对特征点定位的影响,同时很好的描述了瞳孔的运动。
本文第2节详细给出了本文提出的弹性动力学不对等模型和算法,在第3节将本文所提出模型与其他模型的归一化图像类内匹配结果进行比较,通过实验验证了算法的有效性,第4节是文章结语,讨论了本文模型的优缺点以及探讨模型改进的方向。
2. 本文模型
从生理学的角度来看,瞳孔的直径可从1.5毫米变化到7毫米,所引起的虹膜组织在切向上的变化可达到5倍以上(靠近瞳孔附近变化较大),在径向的变化可达到2倍以上,Daugman的橡胶板模型已经不足以表达复杂的虹膜变形物理性质,需考虑房水折射和弹性组织特性引起的虹膜变形。如图1所示,虹膜组织内有环绕瞳孔排列的平滑肌,叫瞳孔括约肌,外有在虹膜外边界附近呈放射状排列的平滑肌,为瞳孔开大肌。光线微弱时,瞳孔开大肌向外扩张,增加光线进入;强光照射眼睛时,瞳孔括约肌向内收缩,减少光亮进入。
2.1. 房水折射
虹膜是位于前房后面、晶状体前面的一个环状组织 [7] ,中间瞳孔的扩张和收缩调节眼球进光量。前房是眼球中角膜后方与虹膜、晶状体前方之间的空腔,其内部充满房水。正常的角膜为球面,可以把前房和角膜的折射看作单折射球面模型 [8] ,采集虹膜图像时,采集仪器与人眼的距离在15~20 cm之间,而虹膜的直径约为12.5 mm,两者差别非常大,所以在虹膜采集过程中,可以把3D眼睛结构看作平行光线的球面折射模型,见图2所示。
观测到的虹膜图像是经角膜和房水折射后的图像,本文根据解剖精确的人眼模型建立三维折射模型,将虹膜重建到它的非折射状态,改善房水折射对初始定位的影响。
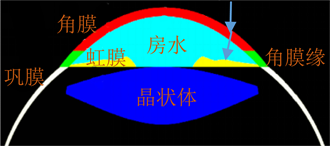
Figure 2. Aqueous humor refraction section diagram
图2.房水折射截面图图
2.2. 虹膜动力学定位
虹膜区域是一个薄圆柱壳,忽略其厚度的影响,将虹膜区域简化为二维极坐标
平面。在极坐标系中,用
表示径向正应力,用
表示切向正应力,
和
分别表示径向和切向的剪应力,
和
分别是沿径向和切向方向上的正应变,
是剪应变,
和
分别为沿径向和切向方向上的位移,其应变位移几何关系 [9] 为:
,(1)
由于虹膜材料是正交各向异性,其应力与应变之间的本构关系式为:
, (2)
其中
和
分别是沿径向和切向方向上的杨氏模量,由虹膜区域的材料特性决定。
是沿切向方向上的泊松比,
是沿径向方向上的泊松比。对于正交各向异性材料,有如下平衡关系:
,(3)
从环形虹膜上的任意位置处分割出扇形微分单元体ABCD,其由两个相距
的圆柱面和互成
的两个径向面构成,进行受力分析,如图3所示,记应力分量由圆心向外和垂直于半径方向向下为正值。
当虹膜图像采集环境稳定时,虹膜处于相对平衡状态,可以得到如下平衡方程:
, (4)
2.3. 虹膜扩张和收缩运动的不对等性
虹膜是一弹性圆环组织,其上每一点的应力分量随位置的变化而变化的,以AB面距离虹膜中心的半径长度r,应力大小
,剪应力大小
为参照标准,当瞳孔扩张时,虹膜组织向外运动,应力
,剪应力
;当瞳孔收缩时,虹膜组织向内运动,应力
,剪应力
。
相对于扇形微分单元体ABCD,有AB面上的应力分量指向圆心为负值,有
,剪应力分量垂直于半径方向向上也为负值
;因此CD面上的应力分量指向无穷远处为正值,剪应力分量垂直于半径方向向下为正值,且相对于AB面上的应力分量CD面上的应力分量和剪应力分量分别为:
同理,当AD面上的应力分量为
和剪应力分量为
时,有BC面上的应力分量和剪应力分量为:
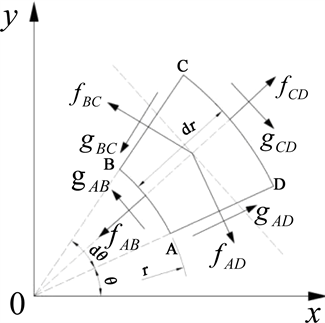
Figure 3. Iris characteristic point force analysis diagram
图3. 虹膜特征点受力分析图
化简(4)式得:
, (5)
光线较弱时,虹膜为保证一定的进光量,弹性组织向外扩张 [10] ,此时虹膜沿径向方向整体所受应力由圆心向外,沿切向方向应力垂直于半径方向向下,均为正值,其平衡方程为:
, (6)
(1)(2)代入上式,化简可得如下控制微分方程边值问题:
,(7)
其中
是虹膜模板的瞳孔半径,
是径向方向的位移,位于半径r处的特征点被移动到位于半径
的最终位置。
强光照射眼睛时,虹膜组织向内收缩,此时虹膜沿径向方向整体所受应力指向圆心,沿切向方向所受应力垂直于半径方向上,均为负值,化简(5)式得:
, (8)
将(1)(2)代入上式,化简可得如下控制微分方程边值问题:
,(9)
通过分析瞳孔扩张、收缩方程知,虹膜组织沿径向方向向外、向内运动,不单单是两个反向力作用的结果,还有剪应力的影响,导致在一对大小相同、方向相反力的作用下,虹膜运动出现沿径向方向内外运动的不对等性。
3. 实验结果与分析
相较于橡胶板模型,本文所提出的虹膜弹性运动不对等性模型,在对房水进行折射偏差校正的基础上,分别研究虹膜扩张和收缩的弹性变化情况。
分别取两组橡胶板模型和本文模型归一化后的虹膜图像,比较类内单行相同灰度值占比,由图4可知,红线大多都位于蓝线的上方,且数值也更接近于1,也即本文模型的归一化效果优于橡胶板模型。
为了验证本文模型对虹膜类内匹配的有效性,此节采用衡量两幅图像相似度指标的算法:结构相似性(SSIM),此算法从图像组成的角度将结构信息定义为独立于亮度、对比度的反映场景中,衡量物体结构的属性,并将失真建模为亮度、对比度和结构三个不同因素的组合。用均值作为亮度的估计,标准差作为对比度的估计,协方差作为结构相似程度的度量,建立质量客观评价标准,评估橡胶板模型、Clark模

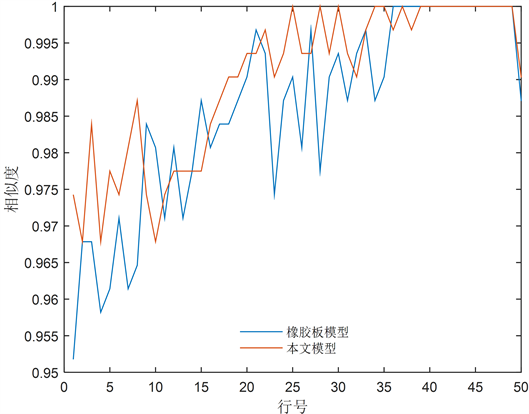
Figure 4. Normalized one-line ratio of the same gray value
图4. 归一化单行相同灰度值占比
型和本文模型的归一化定位效果。相似性度量取值范围为[0, 1],实验随选取1张虹膜图像与其他16张虹膜图像进行结构相似性评估,当评估取值越接近1时,两张图像间的相似性越高,归一化定位效果也越好;当取值趋近0时,两张图像间的相似性较低,可判断两张虹膜图像不属于同一个人,此时会发生类内错误拒绝的情况,也即归一化效果不理想。
从虹膜数据库中随机选取17张虹膜图像进行类内结构相似比较,重复进行四次,前两组为瞳孔扩张状态,后两组为瞳孔收缩状态,比较结果如图5所示。其中橡胶板模型作为经典的归一化方法,基本可以区分类内和类间虹膜,只是精度还有待提升。Clark模型对瞳孔扩张状态归一化效果较好,但当瞳孔收缩时拍得的虹膜图像归一化效果较差,易导致类内错误拒绝的情况发生。本文模型消除了对房水折射的干扰,再在Clark模型的基础上进行改进,由折线图可知,对扩张和收缩状态的虹膜类内结构相似性度量有明显的提升,尤其是后两组瞳孔收缩状态时,本文模型保证了类内结构相似的准确性和稳定性。
对不同光照强度下拍摄的虹膜图像数据集进行归一化结果比较,为避免由于眼睑和睫毛遮挡造成的虚假虹膜信息,选取中间无干扰的虹膜区域 [11] ,并进行效果验证。本文考虑以瞳孔处于正常状态下的虹
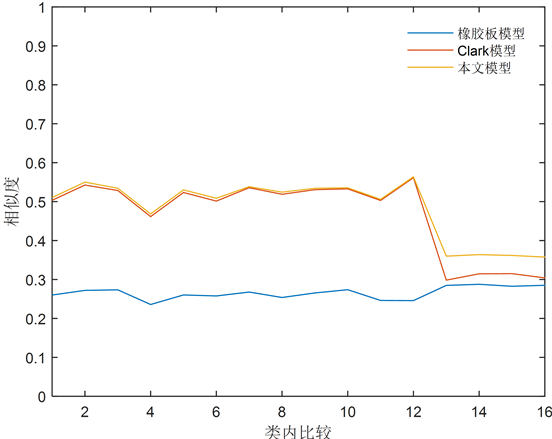

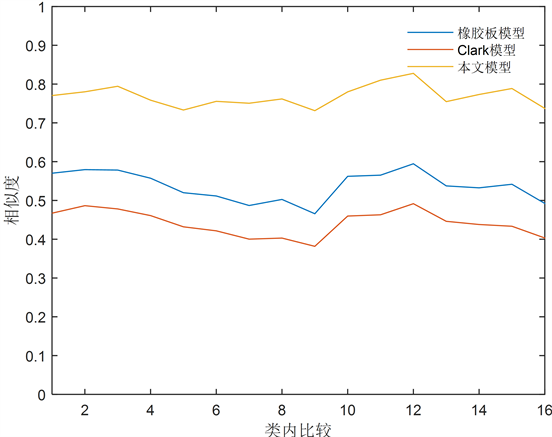

Figure 5. Inner structure similarity of iris image
图5. 虹膜图像类内结构相似度
膜内外圆半径比作为分界线,先对虹膜图像进行房水折射校正,再采用虹膜弹性运动不对等模型,对虹膜进行归一化处理。此折射校正后的弹性运动模型更符合眼球的组织结构和虹膜弹性组织的运动规律,且采用此模型的归一化结果进行比较,虹膜的结构相似性度量有明显提升,类内匹配成功率也大大增加,同时降低了类内错误拒绝率和类间错误接受率。
4. 结语
本文在Clark等提出的虹膜动力学的理论模型的基础上,考虑瞳孔扩张和收缩的不同工作机制,并考虑房水折射的影响,提出了一种结合房水折射和瞳孔扩张、收缩的弹性运动不对等性模型,对虹膜特征点位置进行偏差校正。本模型不仅适用于瞳孔扩张状态,还适用于瞳孔收缩状态,相较于最经典的Daugman橡胶板模型来说,对类内匹配效果有所提升。为了进一步提高虹膜识别性能,若建立基于虹膜生理特性的3D虹膜变形模型,并考虑房水的前后房压差变化对虹膜弯曲面的影响 [12] 和角膜缘的遮挡 [13] 等,无疑会对识别效果产生正面的影响。