1. 前言
压实度指标检测主要是通过检测压实层密度的方法来实现,弯沉、模量指标检测主要是通过检测应力应变的方法来实现,其中检测应力应变的方法又分为动态和静态两种 [1] 。常用点式检测控制 [2] 。为了使检测控制和施工工艺相适应,减少检测时长从而减少对施工工序的影响,提高检测准确性和适应性,实时提供压实结果以提高压实效率,增加检测功能,全面控制压实工艺,需要在路基压实过程中推广、使用连续压实检测控制技术。在二十一世纪,智能压实系统已经进入一个全新的时代,智能系统在铁路方面已经得到应用,也形成了对应的理论实践体系,在公路方面人们正在积极研究,理论和实践方面也在日趋成长,相信这一技术在此方面一定会不断完善,早日为工程人员创造价值 [3] [4] 。
为了对基于智能压实技术对填筑体路基压实度的研究,以白洋淀大道作为试验场地,对在三种土路基材料下,运用MGYS-III连续压实进行分析;对智能压实控制指标CMV与灌砂法得到的压实度值进行相关分析与回归分析 [5] 。
2. 压路机在碾压过程中对填筑体建模求解和分析
2.1. 填筑体为离散体——“质量块–弹簧–阻尼”模型
2.1.1. “质量块–弹簧–阻尼”模型建立与解析
在碾压过程中,塑性变形较大,弹性变形较小。随着碾压遍数增加,塑性变形逐渐减小,弹性变形逐渐增强,一直到碾压结束时,塑性变形消失,弹性变形达到一定值 [6] 。变形过程如图1。
填筑体离散体——“质量块–弹簧–阻尼”模型把压路机滚筒、振动装置、填筑体者耦合建立离散模型,如图2。假设条件为:1) 钢轮与弹簧以及阻尼之间必须紧密接触,不能有弹跳。2) 部分填筑体参与振动,建模应考虑参振质量,但不容易确准确定。如图3为双自由度系统与单自由度系统:
2.2. 振动压路机响应信号处理模拟——谐波比模型
2.2.1. 振动力学模型系统分析
由压路机的振动响应识别路基抵抗力。为了识别路基抵抗力,可作如下假设:由于振动压路机在其内部振子作用下,激励符合简谐振动规律,可将系统简化为不受重力作用的质量M,在瞬时激振力Psinω和抗力F(x)的共同作用下做单自由度的周期运动,对振动力学模型系统进行分析如图4:

Figure 2. Discrete body of filling body—“mass block-spring-damping” model
图2. 填筑体离散体——“质量块–弹簧–阻尼”模型

Figure 3. Two-degree-of-freedom system and single-degree-of-freedom system model
图3. 双自由度系统与单自由度系统模型

Figure 4. Oscillation dynamics model system diagram
图4. 振动力学模型系统图示
2.2.2. 建立振动响应和抗力的相关关系
为了建立振动响应和抗力的相关关系,在已有的单自由度振动力学模型的基础上,还需要建立包含重力作用在内的力学体系。由于振动压路机仅在振动钢轮上产生激振力,将振动轮从压路机体系中分离出来,把振动轮、路基组成独立的激励系统,建立体系。如图5:

Figure 5. Force diagram of excitation system
图5. 激振系统的受力图
根据振动理论,振动压路机在理想状态下(无约束时)振动形态为简谐振动,响应信号呈规则的正弦波形,频率中只有基频成分。当压路机位于被压材料上时,受到来自被压材料的反作用力,随着碾压工作的持续,碾压遍数增加,材料越来越密实,反作用力越来越强,使振动形态不断发生变化,表现为被压材料变形越来越小,波谱越来越复杂,波谱中出现了其他频率的波形,这种波形畸变和材料压实程度之间存在相关关系 [7] 。我们可以通过在复杂的波谱中找到代表振动压路机的激励基频信号幅值和代表被压材料的抗力信号幅值从而确定被压材料实时压实度。通过试验段用标准压实度检验方法和CMV之间的关系,就可以进行实时压实度的检测控制。
3. MGYS-Ⅲ智能压实控制系统实验方法
3.1. 试验工况
于2016年5月在白洋淀大道进行试验,本试验原材料选用保定白洋淀大道地区天然土,根据对现场土的调查,分析土的级配、材料性能等,按照最大粒径的不同将材料分类,选择代表性路段的原材料进行试验。加载设备徐工YZ18JC 18吨压路机;测试设备MGYS-Ⅲ连续控制系统。在三中路基材料下,运用MGYS-III连续压实控制系统连续压实进行计算,得到CMV值,振动频率,机真理,主抗力。结合卫星定位系统厘米级定位可以对接下来的施工路段进行压实度的控制,来反映路基的填料和压实状况,以及压路机振动频率与激振力相关情况。
3.2. MGYS-III系统反映路基的填料和压实状况的分析
3.2.1. 对填料的含水量及压实度的分析
选取白洋淀大道K2 + 610~K2 + 650公路段,土地基,含水量普遍偏高(如图6)。此时压路机的振动参数(如表1)。对此路段连续压实两遍,对反馈回来的振动频率图7(a)以及CMV值时序图分析图7(b)。
根据MGYS-Ⅲ系统反馈出来的振动频率图和CMV值图,可以发现CMV值太小且多遍碾压无明显上升,振动频率也无明显上升,说明土的含水率高,需要对此路段进行翻晒处理。
3.2.2. 对填料的均匀度的分析
选取白洋淀大道K2 + 610土底基有不均匀石料,含水量高,路面相对平整。此时压路机的振动参数(如表2)。单点27 Hz强振15秒对反馈回来的振动频率图8以及CMV值时序图分析图9。

Figure 6. High water content in this section
图6. 该路段含水量高
 (a)
(a) (b)
(b)
Figure 7. (a) MGYS-III feedback vibration frequency; (b) CMV sequence diagram
图7. (a) MGYS-III反馈得到的振动频率;(b) CMV值时序图

Figure 8. Vibration frequency obtained by feedback of MGYS-III
图8. MGYS-III反馈得到的振动频率

Table 1. Vibration parameters of roller at this stage
表1. 此阶段压路机振动参数

Table 2. Vibration parameters of roller at this stage
表2. 此阶段压路机振动参数
3.2.3. 对压实的均匀性的分析
选取白洋淀大道K2 + 210~K2 + 250路段外侧辅路底基 ,土料,底基层未刮平,经过两遍的振压,得到的振动频率图10,CMV值时序图11以及控制终端显示CMV曲线图12。
由上图可以发现,得到的CMV时序图标准差较大(时序曲线波动较大),说明路基填料不均匀。在经过两次振压后,发现第一遍振压和第二遍振压所得到的CMV值变化比较大,说明路基可以继续压实。
4. 智能压实控制指标CMV与压实度相关校验
4.1. 连续压实检测结果选取
4.1.1. 现场取点数据整理
实验地点:白洋淀大道 建筑材料:二灰。

Figure 10. Vibration frequency obtained by feedback of MGYS-III
图10. MGYS-III反馈得到的振动频率

Figure 12. Control terminal displays CMV curve
图12. 控制终端显示CMV曲线图
4.1.2. 曲线拟合的选择
通过插值基函数得到拉格朗日插值多项式,使理论分析便捷,但全部插值基函数随插值节点的变化而变化,使公式随之变化 对于实际计算不方便,为了解决这一点,提出了牛顿插值。牛顿插值通过求各阶差商,递推得到的一个公式 [8] :
只需求出系数ai,即可得到插值多项式。但上式在数据成线性关系时,点数较多时,不适合用来拟合直线,CMV值和灌沙法得到压实度值近似成线性关系,而最小二乘法对于解决这类问题十分便捷,所以选用最小二乘法。直线方程:
。
4.2. 智能压实压实度与CMV值得线性计算
现在计算
和
的相关系数,也就是压实度和CMV值得相关系数。
其中
,
是指数据
,
的平均值。
现在分别计算分子的
,
,
的值。分别计算分母的
,
,
的值。
4.3. 智能压实压实度与CMV值的回归模型计算以及校验预测4.3.1回归模型计算
回归模型一:
用灌砂法测得的压实度值确定CMV值的检测结果回归模型
式中:
x——灌砂法测得的结果,普通填料为地基系数,化学改良土为压实系数;
y——CMV;
,
——x和y分别代表智能压实压实度和CMV值,其中
,代表数据中的数量;
a,b——回归系数。
回归模型二:
用CMV值确定灌砂法测得的压实度值的检测结果回归模型
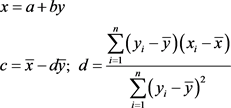
式中:
x——灌砂法测得的结果,普通填料为地基系数,化学改良土为压实系数;
y——CMV;
,
——x和y分别代表智能压实压实度和CMV值,其中
,代表数据中的数量;
c,d——回归系数。
4.3.1. 线性回归模型校验与预测
通过对压实度与CMV值校验与预测,得出下面表3。可发现得到的目标压实值CMV和压实度预测值在误差范围5%内,证明计算得到的线性回归模型的正确,也可以说明此压实系统的准确性 [9] 。

Table 3. Linear regression model check and prediction table
表3. 线性回归模型校验与预测计算表
采用MGYS-Ⅲ智能压实系统,在白洋淀大道北道K2 + 210~K2 + 250路段进行压实处理。通过系统对北道K2 + 210~K2 + 250路段压实度数据采集,提取了北道第二遍、第三遍、第四遍、第五遍的CMV值,并对这些数据进行处理分析。根据线性回归模型预测方程x = 72.804 + 0.31873*y把北道第二遍、第三遍、第四遍、第五遍的CMV值代入到此方程中得到北道第二遍、第三遍、第四遍、第五遍的理论灌砂压实度值。可发现当CMV值达到70左右的时候,此路段压实度值可达到95%以上,说明压实程度达到规范标准。
5. 结论
一、系统能较全面的反映路基的填料和压实状况。
二、MGYS-Ⅲ系统结合卫星定位系统厘米级定位可以对接下来的施工路段进行压实度的控制 [10] 和压实遍数的控制。
三、路基结构抵抗变形能力的度量为常规检测和连续检测。检测结果为统计学上的正相关关系。对整个碾压面的现场可视化的全面监控和检测。
基金项目
河北省住房和城乡建设厅(2016-272)。