1. 引言
在对计量化学、生物信息学、食品研究、医学、药理学等方面的研究时,经常需要从海量的数据中寻找出内在的联系性。这些海量的数据或通过实验得到、或在实践中得到,然而从这些数据的表面上并不能得到很多的信息,必需对这些数据进行进一步的处理。数据通常可以分成两组向量:因变量的向量、自变量的向量,讨论它们之间的内在联系。最简单的情况是:每组向量中均只有一个元素。因变量的向量与自变量的向量可能存在一定的回归关系。这些回归关系一般是非线性的关系,如果不会引起很大的失真性,可以用线性回归的方式近似。最小二乘(Least Square (LS))回归是这些回归模型中常用的处理误差的方法。为了合理、快捷地搜寻数据中存在的内在关系,研究者对最小二乘回归进行了各种改进,较典型的方法有:主成分分析(Principal Component Analysis (PCA))法、核主成分分析(Kernel Principal Component Analysis (KPCA))法与偏最小二乘(Partial Least Squares (PLS))法。核主成分分析法是主成分分析法的变种;偏最小二乘方法是主成分分析法与最小二乘回归相结合得到的一种方法,常称为PLS方法。现有的文献比较多侧重于这些方法的使用,但分析它们的数学原理、类比这些方法的异同处,并通过事例进行讨论的不多见。下面介绍最小二乘法、主成分分析法和偏最小二乘方法的数学工作原理,讨论它们的联系性。
2. 最小二乘法、主成分分析法与偏最小二乘方法的数学原理
2.1. 最小二乘方法
最小二乘方法 [1] 能够对实际问题有比较好的解释,该方法的核心是所有估计值与被估计值之差的平方和达到最小。因变量向量用y表示,自变量向量为x。若只有一个因变量,则此时的最小二乘方法即为最简单形式的最小二乘的曲线拟合,给定m个合适的函数
及n组数据
,其中
表示因变量、自变量组
的第i组值。为了方便,记
为
。选定适当的参数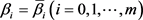 ,得到曲线
,得到曲线
,s.t.
.
在没有其他限制条件下,
关于
的一阶偏导为0是得到
的极小值的必要条件。选取参数
的数学工作原理如下:
令
,
,分别求L关于
的偏导数,并令其为0,即
计算可得
(1)
其中,
。
选择合适的函数
并不容易,常简化曲线拟合为线性拟合或多项式拟合,最简单的模型为线性回归模型,即因变量y是自变量
1的线性组合:
, 其中
.
给定n组数据
,待定的系数
使得误差平方的叠加和最小,易得出
当
时,
其达到最小值,此时
,
其中
,
。
线性回归模型
是最简单的数据处理模型,不一定能够真正反映实际数据的内存规律;最小二乘方法涉及所有的变量,不同自变量数据之间可能存在全部或部分线性相关性关系,这时数据的有效信息可能不能直接体现出来。减少线性回归模型的变量的个数,但又不要丢弃太多的信息,主成分分析方法 [2] [3] 是可选方法之一。
2.2. 主成分分析法
针对不同自变量数据之间存在全部或部相关性关系,导致(1)式中
成为病态矩阵,不再适合用最小二乘方法,W.F. Massy [3] 提出了主成分回归(Principal Component Regression,简称PCR)方法。主成分分析的核心在于降维,将原有的多个性能指标(即多个自变量)减少为只含有少数几个综合性能指标。这些综合性能指标是原来的性能指标的线性组合,它们相互独立且集中反映出原始变量的较多信息,在选择综合性能指标时,一般通过信息量与原有信息量的百分比(如95%或更多、更少的百分比)来衡量。
设x是有n个随机变量组成的列向量2,研究它们所体现的信息,通常得计算出这n个随机变量的方差、协方差,找出这n个随机变量间有意义的相关性结构。然而若n较大,计算向量x的方差、协方差要花费比较多时间,除非n很小或者变量之间的相关性结构很简单,否则发现随机变量间的相关性结构比较困难。研究随机变量隐含的信息时,考虑研究一些维数远远低于n的派生变量,这些派生变量是原来变量的线性组合,它们保留了原来变量绝大部分信息,这样的派生变量称之为主成分。
主成分分析法中,寻找主成分的步骤如下3:
第一步:寻找第一个主成分,即找出x的一个线性组合
,记为
,其中
是一个n维列向量,
,
,
为
的方差。
,
s.t.
最大,且
。
第二步:寻找第二个主成分,也即寻找x的第二个线性组合
,记为
,其中
是一个n维列向量,
,
,
,
s.t.
最大,且
,
与
线性无关。
以此类推,直至找到线性关系
,使其与
线性无关且具有最大方差。至此,k个主成分找到了。
第三步:建立因变量与主成分的回归方程,其中最简单的是线性回归方程。可依据最小二乘回归得到数学模型。
获得主成分的数学推导过程描述如下。
两个随机变量具有线性无关性,是指两个随机变量之间的协方差为0。在寻找主成分前,先对随机变量的数值进行规范化处理,使得随机变量的均值为0,方差为1。设随机变量的向量x的协方差矩阵为
。
对于第一主成分
:利用Lagrange乘子法,构造Lagrange函数
,
其中λ是Lagrange乘子,依据极值原理,
是在条件
时
的取得最大值的充要条件。上式两边对
求导,令其为0,即
其中
是n阶单位矩阵。显然λ是
特征值,
是相应的特征向量。由于
,所以
。因此,第一主成分中出现的系数为协方差矩阵
的最大特征值
的特征向量
。
对于第二主成分
:由于
线性无关,故
,而
,从而有
利用Lagrange乘子法,构造Lagrange函数
上式两边对
求导,令其为0,即
(2)
两边左乘
,得
代入(2),得
,显然λ是
的特征值,
是相应的特征向量。由于
,所以
。假设
没有重根,则
,
是
的第二大特征根,相应的特征向量
是第二主成分中出现的系数4。
类似地,可以依次从大到小求出
的其它特征根及特征向量,找出相应的主成分,通常依据
确定从
所有t个特征值
中选取s个特征值
。
2.3. 偏最小二乘法
偏最小二乘方法 [4] [5] [6] [7] [8] 是20世纪80年代从应用中总结出来的一种降维技术。偏最小二乘回归方法的一大优点是:考虑样本总体对预测值的影响程度时,也充分考虑了单个因素间的综合作用对预测的影响。在回归速率上,偏最小二乘方法比一般的多元回归方法更快一些,对样本的要求更加宽松。偏最小二乘回归方法可以看成是最小二乘回归、主成分方法及典型相关分析方法的综合体。
偏最小二乘方法的原理如下:
设X5是含有n个随机变量
组成的自变量的列向量,Y是含有一个或多个随机变量
的因变量的列向量。找出X的k个线性组合
,这些线性组合满足主成分分析的要求;在Y中找出r个线性组合
,它们也满足主成分分析的要求。建立
与
的回归关系,使它们之间的相关程度达到最大;并构造
与
的回归关系,建立Y与X的回归关系。
偏最小二乘回归分析的步骤:
第一步:分别找出X与Y的第一主成分
,并且使
的协方差
达到最大。
,
s.t.
, 且
.
,
s.t.
, 且
;
.
上述的方法在推导过程中,作了如下假定:1) 各变量的特征维数不大;2) 过程不存在序列相关性;3) 过程是线性的。以上方法中要求X及Y均已经作了预处理,使X及Y中心化、均值化。
第二步:先建立
与
的回归关系:
,其中W为相应的权值;由
与X的线性回归方程及τ与Y的线性回归方程,得到
与Y的线性回归方程。
当
均为0时,显然有
,
,
;一般地,
分别是这些回归方程的残差矩阵。
第三步:分别用
替换
,重复第一步~第二步,依次寻找X的第二主成分
。类似地,依次得到第三主成分
,…,第d个主成分
。
由第二步得到Y与X的主成分β的回归关系式:
,利用第一步中的结果,容易得到Y与X的回归关系。
下面对第一步作详细分析,利用Lagrange乘子法求解
。
令
,
由于
,
所以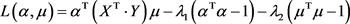 ,
,
依据极值原理,
关于
在边界上取得极大值的充要条件为相应的偏导数为0。下面分别对
求偏导,得
(i)
(ii)
所以由(i),(ii)可得
注意到
。
由此可得出,
是矩阵
的最大特征值所对应的特征向量,也是X的第一主成分
的系数部分;
是矩阵
的最大的特征值所对应的特征向量,也是Y的第一主成分
的系数。
采用PLS进行计算机处理数据时,常常通过迭代方式进行。在n维空间中任意选取一个非零列向量u (与列向量Y有相同的维数的向量),PLS回归迭代过程包括6个步骤 [3] :
如果Y是一维向量,我们用y表示Y,此时有
;当满足精确度要求时,迭代步骤停止。可以证明w是
的近似值,c为
的近似值,说明如下:
设最初选取的非零向量为
,第一次利用PLS的6个步骤的1) 3) 4) 6)得到的为
;由
利用PLS的6个步骤的1) 3) 4) 6)得到的为
所以
类似地,有以下式子成立
3. 比较最小二乘方法、主成分分析法及偏最小二乘法
最小二乘方法、主成分分析法与偏最小二乘方法,均是从误差最小化方面去寻找合适的参数。这些方法在处理误差时,都默认了误差分布是理想的 [1] ,即模型误差是独立同分布的且服从其均值为0、方差为
的正太分布。下面以最小二乘方法进行说明。
给定需要拟合的数据
,利用下面的多元回归模型(即因变量关于自变量的数学期望)进行数据拟合:
,利用最小二乘估计得到参数
,每组拟合数据
均满足方程
其中
是模型的随机误差,它独立同分布,服从均值为0,方差为
的正太分布。
这里考虑因变量是自变量的多元线性回归模型,且只有一个因变量。从上述描写可知,在利用最小二乘法时,要求
可逆。如果X的列之间存在多重共线,纵然
可逆,由(1)计算得
建立的数学模型,很可能不具有通用性。
X的列之间存在多重共线时,利用主成分分析法可消除这种共线性的不良影响。主成分分析法从原有的自变量向量中寻找它们的某些线性组合(即综合的指标或称之为综合自变量),在信息损失最小的原则下,得到少数几个综合自变量。主成分分析法可以在一定程度上消除了原自变量之间的多重共线性,而且降低了待处理数据的维数。处理有周期性变化规律的数据时,如经济运行中的得到的各类经济数据,主成分分析法与谱分析方法相结合 [9] ,分析数据的变化趋势与规律。
主成分分析法对X进行主成分分析,没有考虑因变量Y,也没有考虑X对Y的解释作用。PLS方法解决了这种缺憾。PLS回归(Partial Least-Square Regression,简称PLSR)方法充分利用了PCR方法对信息(自变量数据)提取的思想。
PLSR方法是S. Wold和C. Albano [4] 在1983年提出的。许多研究工作者 [5] [6] [7] [8] 对PLSR进行了研究,他们还研究了利用迭代的方式计算主成分(参考上文中“PLS回归迭代过程”关内容)。PLSR是主成分分析法与最小二乘法的综合体,它对自变量和因变量均提取主成分,同时还考虑了因变量的作用以及自变量X对因变量的解释作用,一定程度上消除了基于主成分的回归模型的不可靠性。
如果响应变量类似于二值情况,回归模型的随机误差
明显不是理想状态,即
不服从均值为0、方差为
的正太分布。此时均值与方差均可能是随着自变量而发生改变,不可以利用多元回归方法中的最小二乘法来解决问题 [1] 。例如,Logistic回归模型是一种比较理想的对二值响应的拟合,可以利用梯度下降法得到Logistic回归函数中的待估参数。
4. 拟合回归模型优良性检验说明
对于已经给的数据分析研究得到相应的回归模型时,通常只需要作参数检验 [1] ,检查
或
6。如果得到的多个自变量数据与正交性差距太大,即它们明显不具有正交性,那么得到的模型可能过度拟合,此时需要进行交互验证 [1] 。我们下一步要做的工作是针对具体问题,利用前述方法建立模型并进行参数检验与参数在实际情况的意义的解释。
附录
定理[1]:对于线性回归方程
,
方差
的无偏估计可由下面的均方误差或均方残差
给出,即
,其中
,
其中ε是一个服从均值为0、方差接近于0的正太分布的随机变量,k为自变量的个数,n为数据组的个数,
与
分别是因变量y的第i个的观测值与模型估计值。
平方和等式
中,
为因变量y的n个观测数据的平均值;SSR的自由度为k,而SST的自由度为
,因此SSE的自由度为
。
下述系数
是用来衡量拟合回归模型优良性的一个常用指标
................线性回归方程所解释的变差占总变差的比例。
...................依据自由度调整后的R2值。
NOTES
1如果只有一个自变量,则n = 1。
2这里的x已经标准化,即已中心化、均值化。
3尽管主成分分析没有忽略协方差和相关性,但是更注重方差。
4协方差矩阵
为实对称矩阵,依据线性代数相关知识,可得
中属于不同特征值的特征向量必定线性无关。
5此处的X、Y与(1)式中的X、Y含义不同。
6
或
含义见附录。