1. 引言
近几年来,随着科学技术的迅速发展,三阶微分方程边值问题在诸多领域都有显著的实用价值,尤其在工程、军事、医学及生态等领域发挥着重要的作用,如三阶微分方程边值问题刻画三层梁及带有固定或变化横截面的屈曲梁的挠度,见文献 [1] 。由于其重要的应用背景,三阶微分方程边值问题(正)解的存在性及多解性也备受诸多学者的关注,并且获得了丰硕的成果(见 [2] - [9] 及其参考文献)。
1994年,P. Kelevedjiev [10] 运用Leray-Schauder原理证明了障碍带条件下非线性二阶两点边值问题
解的存在性。2008年,杜睿娟 [2] 在障碍带条件下研究了非线性常微分方程三阶两点边值问题
(1)
解的存在性,并获得了如下结论:
定理1:设
连续,假定存在常数
。满足
,使得
及
成立,则边值问题(1)在
中至少有一个解。
2009年,张宏旺 [3] 运用新的极大值原理及上下解的单调迭代法获得了非线性三阶边值问题
解的存在性结果。2016年,蒋志丽,杜娟 [4] 通过构造迭代的方法证明了如下非线性三阶边值问题
解的存在性。
受文献 [2] - [7] 的启发,本文探讨在障碍带条件下的两类非线性三阶两点边值问题
(2)
和
(3)
解的存在性,其中
连续,A,B,C为给定的常数。
2. 预备知识
令
表示区间
上连续函数构成的空间,定义其上范数为
。记
,其上范数为:
则
按范数
构成Banach空间。
记
分别为满足问题(2)和(3)中边值问题的函数构成的集合,并令
。
定义算子:
如下
显然,
为一一映射。
本文主要工具为Leray-Schauder原理:
定理2:令E为Banach空间,设
为全连续算子。若
有界,则A在E的闭球B中必有不动点,这里
,R满足
。
3. 主要结果及证明
定理3:设
连续,假定存在常数
使得
其中
,满足

则问题(2)在
中至少存在一个解。
证明:考虑同伦族问题:
(4)
显然,
是一一映射。因此,运用定理2,若问题(4)的所有可能解u在
中有一个不依赖于
的先验界,即存在正常数
,使得
,则问题(2)在
中有解。
设
是问题(4)的一个解。则由微分中值定理得,存在
,使得
。同理,存在
,使得
因此,
为证
,首先估计
的界。
假设集合
非空。取定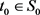 ,
,如果存在
,
使得
,
,如果存在
,
使得
(5)
由
的连续性,甚至可以取到
,
,但对
,有
所以
。同理,对
,有
,这与(5)矛盾!从而
特别地,
,这与
矛盾,所以
与
是空集。
因为
在
上连续,所以存在
,且
同理,由条件
可得
。因此,对任意的
,有
(6)
其中
。
其次,估计
和
的界,对每一个
,存在
,使得
由此得
(7)
其中
。
对每个
,存在
,使得
由此得
(8)
其中
。
最后,由于
,f连续,
,所以
(9)
其中
是不依赖于λ的常数,结合(6),(7),(8),(9),则
故问题(2)在
中至少存在一个解。
对偶地,通过类似的讨论,可获得如下问题(2)解的存在性结果。
定理4:设
连续,假定存在常数
,使得
,其中
,满足
则边值问题(2)在
中至少存在一个解。
注5:定理3与定理4对问题(3)也成立,只需取
。
注6:边值问题(2)或(3)中的边值条件中A,B,C取零时,上述结论仍然成立。
注意到,定理3,定理4中的非线性项ƒ满足障碍带条件是在区间上给出的,自然地,当区间退化为一点时,是否仍然能获得边值问题(2)或(3)解的存在性呢?下面我们给予肯定的回答。
定理7:设
连续,假定存在常数
满足
,使得
则边值问题(3)在
中至少存在一个解。
证明:由Tietze-Urysohn引理,存在连续函数
,使得
对任一正整数m,令
,显然
连续。考察辅助边值问题
(10)
易见
,从而由连续函数的保号性知,存在
满足
,使得
同理,存在
满足
,使得
显然,选取区间如下:
(11)
(12)
类似定理3的证明可证得,边值问题(10)在
中有解
,且满足
因此,存在常数
,使得
(13)
由微分中值定理,对任意的
,存在
,使得
则存在正的常数
,使得
(14)
同理,存在正的常数
,使得
(15)
则由(13),(14),(15)及(10)得,存在不依赖于λ的正常数
,使得
(16)
结合(13)~(16),易证
。
下证问题(10)的解序列
存在一收敛子列
,满足
且
是边值问题(3)的解。
事实上,由于
紧嵌入
,若
在
有界,则
是
中的相对紧集,则存在
,满足
又
有界,且
紧嵌入
,故存在子序列
,满足
同理存在
,满足
不妨记
,则
满足边值问题
(17)
显然问题(17)等价于积分方程
(18)
其中
为边值问题(3)的Green函数。因为
收敛到f,且
连续,故对(18)两端取极限,可得
,从而
,且满足问题(3)。
类似地可证下面对偶问题成立。
定理8:设
连续,假定存在常数
满足
,使得
则边值问题(3)在
中至少存在一个解。
注9:定理7,8对边值问题(2)也成立,只需
满足边值问题(17)的边值条件替换为
,且问题(17)等价于积分方程
其中
为边值问题(2)的Green函数。
例10:考虑三阶两点边值问题
(19)
其中A,B,C为任意常数,
。
易见,令

不难验证
满足定理3的所有条件,因此边值问题(19)在
中至少有一个解。
例11:考虑三阶两点边值问题
(20)
其中A,B,C为任意常数,
。
易见,取
,不难验证
满足定理8的全部条件,因此边值问题(20)在
中至少存在一个解。
基金项目
国家自然科学基金数学天元项目(11626188),甘肃省年科技基金计划项目(1606RJYA232),西北师范大学青年教师科研能力提升计划一般项目(NWNU-LKQN-15-16)。