1. 引言
1.1 背景
图像的传播利用与人们的生活密切相关。然而,受传输过程中硬件性能的局限,经过传递后的图像可能会产生降质,如携带噪音、产生模糊或者缺损等等。为了得到比较理想的图像,人们需要对这些退化了的图像进行一些处理。基于变分法的图像处理方法是一类重要的方法,已经被广泛研究,例如,基于变分法的图像去噪 [1] [2] [3] [4] [5] 、图像平滑 [6] [7] 、图像去模糊 [8] [9] [10] [11] 、图像填补 [12] [13] 等等。本文针对不同的图像处理目的,列出几种带有不同正则化项的变分图像处理方法加以分析和比较,揭示其中的规律,以便于更进一步的研究。
1.2. 数字图像
本文所研究的图像均指数字图像,着重研究对灰度图像和RGB图像的处理问题。灰度图的每个像素点上只有一个采样,而该采样的值的取值范围是0~255,将取值为0时的黑色和取值为255的白色之间划分成256个灰度级。而RGB图则包括红色、绿色、蓝色三个通道,每个像素点对应一个向量(R, G, B),分别代表该点在“红、绿、蓝”三个通道上的灰度值。每个通道的最大亮度级是255,而通道中的最小亮度级是0。
定义在平面几何区域Ω上的数字图像在数学上用一个空间二元函数
表示,其中
,
。为方便研究,通常选Ω为矩形区域,这时,灰度图和RGB图分别用一个二维矩阵和三维矩阵表示。
1.3. 图像复原
图像复原指的是用各种方法对降质的图像进行处理,从而尽可能地恢复原始图像的图像处理过程。常见的图像复原方法有:图像去噪、平滑、去模糊和填补等等。本文以图像去噪为例,研究一幅带有加性噪音的图像
(1)
其中,f指的是带有噪音的降质图像,u表示未受噪音污染的原始图像,而n代表一个均值为零的高斯白噪音。图像去噪的目的就是建立一个数学模型,以f为基础反解出u。图像处理的效果很大程度上取决于所建立的数学模型。即使对同一幅图像,利用不同的数学模型,求出的结果可能会有很大的差别。所以,图像复原的前期,人们必须尽量利用已知的先验信息来建立一个恰当的数学模型。
建立好模型后,图像复原就成了数学上逆问题的求解。最简单的求解办法就是用最小二乘法,即求解如下的最小二乘模型
(2)
这里,f指的是降质的图像,u代表将要被复原的图像。(2)式的目的是不让被复原的图像偏离降质图像太多,但这可能会造成图像的过度拟合。而且,由于(2)式的目标项没有其它的约束项,所以得到的结果可能不唯一。因此,最小二乘法是一个不适定的方法,通常还需在(2)式中添加具有先验约束作用的正则化项来提高复原效果。本文介绍三种常见的正则化图像处理方法,分析比较三种处理后结果的特点,以便于有针对性地选择合适的正则化项来处理图像。
2. 正则化图像复原方法
2.1. Tikhonov正则——用图像梯度的L2模的平方做正则化项
图像的边界给人们提供了非常重要的视觉信息,因此,在图像复原时,所提出的模型要能够尽可能地保留这些边界信息。而图像边界的梯度一般是比较大的,于是人们考虑对图像梯度加以约束。首先取梯度的L2模的平方最小作为正则约束条件,转换为无条件的近似问题就是如下模型:
(3)
其中,第一项称为Tikhonov正则项,第二项是保真项,λ是一个用来平衡正则项和保真项的正常数,当λ趋于无穷大时,模型(3)的解就可以无限接近约束最小化问题的解了。为求解Tikhonov正则化模型(3),我们求解其对应的Euler-Lagrange方程
(4)
对(4)式做离散化处理。
假设平面矩形区域有
个像素点,利用向前差分将拉普拉斯算子离散为:
,
,
对边界进行镜像延拓得,
,
,
类似可得当
时拉普拉斯算子的离散化表达式。
于是,由(4)式离散解得:
设
,利用Jacobi迭代法求解u,有:
(5)
结果见数值算例1。由算例1可以看出,去噪的同时带来很大的模糊。
2.2. Total Variation (TV)正则——用图像的TV模(即图像梯度的L1模)做正则项
2.2.1. 背景
由于Tikhonov正则化项可导,因此Tikhonov正则化模型比较简单易求。但是由数值算例1可以看出,该方法在去除图像噪音的同时会产生很严重的模糊。为了克服这个问题,1992年,Rudin,Osher,和Fetamin等人提出了一种新的正则化模型——ROF (分别取三人姓名的首字母)模型 [1] 。ROF模型采用图像梯度的L1模做正则约束,即
(6)
其中
是u的梯度的L1模,也称为u的全变分(total variation,简写为TV)。因此,(6)式所代表的模
型被称为基于TV的正则化去噪模型。TV正则项的引入使得在获取最佳图像的同时要限定总变差最小,因此,图像中的水平或者铅直的边界会被很好保持。相比用Tikhonov正则化去噪,用TV正则化模型去噪,效果更好模糊更少。ROF模型具有保持边界的良好性质,自提出以来受到了广泛地关注,大量的学者提出了多种改进的求解方法。2004年,Chambolle [2] 提出一种对偶投影法求解ROF模型。该法将TV正则化模型(6)对应的欧拉–拉格朗日方程做等价变形,把原始问题的求解转化为对偶空间上的一个投影问题的求解。该法简单快速,去噪效果很好。传统的去噪方法在去除噪音的同时都会丢掉一些有用的细节信息,为此,Osher等人2006年提出了一个基于Bregman距离的Bregman迭代规则算法 [3] ,该法在每次迭代求解时都会加入前一步处理中丢弃的噪音。因为在被丢弃了的噪音项中会包含图像的部分边界和细节信息,所以,加入这些被丢弃的信息,就可能会使后面的结果更接近原始图像。鉴于噪音较重时直接回带去除噪音效果不理想,2017年童将Bregman迭代规则算法和Chambolle的对偶投影法结合提出了一个加权噪音回带的去噪音模型 [4] ,该法先给Bregman迭代规则算法的噪音回带项配以一个权重系数,然后再用Chambolle的对偶投影法来求解每一单步,去噪效果优于两种方法中的任意一种方法。本文的TV正则化部分的算例都将用此法实现。
为了将两种方法统一起来,童将加权去噪算法的目标方程变为:
(7)
2.2.2. 算法
2.3. 稀疏正则——用梯度的L0模做正则项
2.3.1. 背景
前面,我们介绍了两种正则化的去噪方法:Tikhonov正则化去噪法和TV正则化去噪方法。这两种方法分别以图像梯度的L2模的平方和图像梯度的L1模作为正则项。Tikhonov正则化模型具有一定的去噪能力,但是会带来很大的模糊,而TV正则化去噪模型能够有效去除噪音并保护水平和铅直边界。为了更好的提取图像的边界信息,2011年,徐立等人提出了一种基于图像梯度L0模的正则化图像稀疏平滑模型 [6] 。该方法以图像梯度的L0模作为正则项,对总体梯度的非零数加以限定,不仅可以平滑掉内部低幅细节和纹理而且还能有效地保护图像的全局主要边界,从而提高了图像边界的识别度,便于边界检测等更进一步的图像处理。2018年何等人提出了一个截断L0正则化平滑方法 [7] ,改进了 [6] 的结果。本文我们着重介绍文章 [6] 提出的梯度的L0模图像稀疏平滑模型:
(10)
其中,I为输入图像,S为平滑后的图像,
代表非零梯度的个数(即梯度的L0模)
 (11)
(11)
2.3.2. 算法
通常,梯度的L0模计算比较困难,徐等人给出了一种的精巧的稀疏梯度计数格式,使L0模最小化问题(10)得到了很好的解决。
首先,引入两个辅助变量
替换
,将目标变为:
(12)
这里,β是一个自适应参数,用来控制
和
的近似程度,其值越大,误差越小。引入分裂迭代法,对(12)的求解转化为两个子问题的迭代求解。
子问题1:计算S
将目标函数(12)中含S的项分离出来,得到子问题
(13)
利用快速傅里叶变换,算出
(14)
上式中的F表示快速傅里叶变换,
表示复共轭,
表示狄拉克函数的傅里叶变换。由于引入了快速傅里叶变换,(14)式只需在傅里叶域上的进行做逐个像素的加、乘和除法运算而不需要处理矩阵逆的问题,因此比原始方程的求解更简单。
子问题2:计算
新的子问题为:
(15)
此时, 返回
的非零元素个数。将上式中的最小化问题转化到在每一个像素上处理,然后再连加得:
返回
的非零元素个数。将上式中的最小化问题转化到在每一个像素上处理,然后再连加得:
(16)
此时,正则化函数变成了一个二值函数:
(17)
3. 数值算例
算例1. 用三种模型分别对256 × 256个像素的Lena灰度图做测试,结果如图1所示。左上图是加了高斯白噪音的Lena图,噪音均方差为12。右上图显示的是用Tikhonov正则化方法做了10次迭代计算后的结果,这里,我们取
。左下图是用TV正则化去噪方法处理的结果。在TV正则化算法中,取
,做了1次外部Bregman迭代和10次投影迭代。右下图是用L0平滑方法处理的结果,我们使用徐立的代码计算,调用L0 Smoothing函数时,取平滑参数为0.005,
。通过比较我们发现,Tikhonov正则化方法去噪图像有明显的模糊。而TV正则化方法不但可以较好地保持大部分的边界,没有造成太大的模糊。用L0正则化法求解后可以抹掉细节并且可以很好地保持边界。
算例2. 仿照算例1,对512 × 512个像素Lena的RGB彩色图像进行了处理。分别在R、G、B三个通道上调用L0Smoothing函数进行平滑(参数设置同算例1),再调用cat( )函数将各个通道的处理结果合并,结果见图2。
算例3. 本算例对两幅545 × 500个像素的蝴蝶花和虞美人花分别进行了L0平滑实验,结果见图3。图3中第一行左右两边各是蝴蝶花和虞美人花。第二行给出的是用L0平滑方法处理的结果,蝴蝶花瓣上大部分比较浅的细小线条被抹去了,主要边界被完整地保留;而虞美人花瓣上大部分不规则纹理也被平滑掉了,较大的纹理边界被保留了下来。第三行是利用sobel算子提取的边界取反后的得到的边界图像。
算例4. 考察L0平滑方法对噪音的敏感性,结果见图4。图4第一行(a)图是256 × 256的Lena原图,(b)-(f)是带不同程度噪音的六幅图,其噪音水平见表1。图4中第二行和第三行分别是调用L0 Smoothing函数对第一行图像的平滑结果,平滑参数分别取0.005和0.01,其PSNR值见表1第二、三行。容易看出,当平滑参数取0.005时,对低噪音平滑效果比较好,而对高噪音图像的平滑效果较差;二当平

 左上图:256 × 256个像素的Lena图像;右上图:Tikhonov正则化去噪结果;左下图:TV正则化去噪结果;右下图:L0稀疏正则化结果
左上图:256 × 256个像素的Lena图像;右上图:Tikhonov正则化去噪结果;左下图:TV正则化去噪结果;右下图:L0稀疏正则化结果
Figure 1. Noisy image and the processing results of a gray image
图1. 噪音图和处理结果
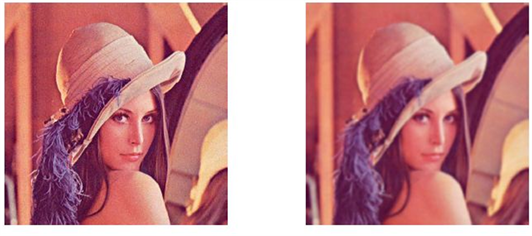
 左上图:512 × 512个像素的图像,添加了均方差sigma = 12的高斯白噪音;右上图:Tikhonov正则化结果;左下图:TV去噪结果;右下图:L0平滑结果
左上图:512 × 512个像素的图像,添加了均方差sigma = 12的高斯白噪音;右上图:Tikhonov正则化结果;左下图:TV去噪结果;右下图:L0平滑结果
Figure 2. Noisy image and the processing results of a RGB images
图2. RGB Lena图像的噪音图和处理结果

 第一行图:545 × 500个像素的两幅图像;第二行图:L0平滑的结果;第三行图:对平滑后的图像提取的边界
第一行图:545 × 500个像素的两幅图像;第二行图:L0平滑的结果;第三行图:对平滑后的图像提取的边界
Figure 3. L0 smoothing and sketching
图3. L0平滑和边界提取
 第一行:待平滑的图像,噪音程度见表1第一行;第二行:平滑参数取0.005时的平滑结果,PSNR值见表1第二行;第三行:平滑参数取0.01时的平滑结果,PSNR值见表1第三行
第一行:待平滑的图像,噪音程度见表1第一行;第二行:平滑参数取0.005时的平滑结果,PSNR值见表1第二行;第三行:平滑参数取0.01时的平滑结果,PSNR值见表1第三行
Figure 4. Images with different noise levels and their L0 smoothing results
图4. 带不同程度高斯白噪音的图像及其L0平滑结果

Table 1. Noise levels and PSNR values after L0 smoothing (unit: dB)
表1. 噪音程度及L0平滑后的PSNR值(单位:dB)
滑参数取0.01时,对高噪音的图像平滑效果相对较好而对低噪音图像的平滑效果不好。但总的来说噪音越重平滑函数对噪音的去除效果越差。
4. 结论和展望
本文讨论了三种正则化图像处理方法,其中Tikhonov正则化方法对噪音去除有一定的效果,但是,由于它是对中心像素周围像素做加权和,因此会带来图像的模糊。而TV正则化方法,由于运用了图像梯度的L1模,所以在去除噪音的同时能保持图像的边界和细节,尤其是水平和铅直边界。TV正则化去噪法的去噪效果非常明显,同时不会引起严重的像素模糊,因此是比较好的去噪方法。而L0平滑法能够去除图像的大部分细节,保持全局主要边界信息,有利于对图像进行轮廓提取或者对图像做版画处理等艺术加工,但是对噪音比较敏感。
本文仅以图像去噪为例,只针对三种具有单一的正则项的模型进行了讨论。未来还可以对以下两方面问题进行探讨:
1) 含有其他单个正则项的方法;
2) 含单个正则项的图像处理模型和含多个正则项的图像处理模型的对比分析。
致谢
本文工作得到了四川省教育厅科研项目(17ZB0447)的资助。