1. 引言
影响海洋磁力测量的误差来源较多,是各种因素综合的影响 [1]。在海洋磁力测量中,就海面船载磁力测量而言,由于受测量平台动态性的影响,海洋磁场观测量除了受到通常的仪器观测误差、海洋磁力测量实施过程中的误差、拖鱼定位误差和正常场校正误差的影响外,还增加了固有的地磁日变改正、船磁改正以及拖鱼位置归算误差的影响,数据处理和公式算法所产生的误差 [2]。从测量过程看,海洋磁力测量误差包括实时测量误差和非实时测量误差。前者指实时定位和磁测所需要的有关参数的测量误差;而后者则是数据处理后所需数据的测量误差或算法等因素所产生的误差。海洋磁力测量准确度以主、联络测线相交点的测量值差的均方根值作为衡量依据 [3] ,而交点处测量值的准确性受上述诸多因素的综合影响。本文针对不同比例尺误差精度进行分析,根据误差传播定律建立了海洋磁力测量中误差关系模型,对影响海洋磁力测量的误差进行分析,探讨了各项误差在不同等级的海洋磁力测量中误差的精度要求变化规律,并给出相应的减小误差的方法。
2. 实时测量误差(T0)
海洋磁力测量中,实时测量误差主要指由仪器系统产生的误差,包括GPS、磁力仪系统产生的测量误差,这类误差一般成系统性。
海洋磁力测量中,海洋磁力测量定位数据的采集由船载GPS定位系统完成,GPS的选择应该尽量满足海洋磁力测量的精度要求,并应该充分考虑测区的地理条件和经济合理性。现阶段的海洋磁力测量定位系统大多采用差分GPS设备,其定位精度可达到厘米级,可以满足各种精度要求的磁力测量,很大程度上消除了定位系统产生的误差。
现代海洋磁力仪按工作原理可以分为质子旋进式、欧弗豪塞(Overhauser)式和光泵式磁力梯度仪等3种不同类型 [4]。海洋磁力测量的磁测数据的采集包括海上磁测部分和日变站磁测部分海上的磁测数据由海洋磁力仪完成。日变站的磁测数据由地磁日交仪完成,因此,磁力仪误差也相应的包括海洋磁力仪误差和日变站磁力仪误差。不同等级的磁力测量,对海洋磁力仪的糖度要求是不同。而地磁日变仪的精度要求应与海洋磁力仪相匹配,随着磁力仪的不断更新和技术改进,磁力仪的磁铡精度不断提高。
针对现今世界市场上海洋磁力仪产品型号较多、技术指标复杂、应用范围不尽相同,产品的选用存在一定困难等问题,标准质子旋进式海洋磁力仪灵敏度较低,存在进向误差,但无死区,价格最为低廉,适合于对灵敏度要求不高的工程和科研地球物理调查。Overhauser海洋磁力仪的灵敏度高,无进向误差,无死区,价格便宜,适合于大多数工程和科研地球物理调查。光泵式海洋磁力仪灵敏度和采样率最高,梯度容忍度最大,但存在死区和进向误差问题,适用于高精度的海洋磁力梯度调查和航空磁力调查。标准质子旋进式海洋磁力仪由于其灵敏度较低,在国内海洋工程和科研地球物理调查中已经较少使用。总体来说,Overhauser海洋磁力仪和光泵式海洋磁力仪各有优势,Overhauser磁力仪一般小巧轻便,价格适宜,而光泵磁力仪采样速度更高一些,梯度容忍度更大一些,因此具体选用应以具体情况而定来减小误差。
测量仪器的误差还存在于晶体振荡器的调试、传感器配谐的调试、静态下仪器信噪比测定与要求、仪器系统的稳定性和仪器系统的稳定性中。进行稳定性测定,若频率漂移,应调试或者更换。测定传感器配谐和选频放大器的每一档中心频率,不满足技术指标时,应更换软件。仪器调试后测量其信号电平值与噪声电平值,信噪比应不小于50,负责要继续调试。调试后的仪器系统进行持续工作状态试验,试验持续时间2d~3d,仪器系统应保持稳定状态 [3]。
3. 非实时测量误差Ti
在海洋磁力测量中,为了得到测点的磁异常,还会有各种非实时测量误差,包括由仪器产生的非实时测量误差、拖鱼位置误差、正常场校正误差、船磁校正误差、日变校正误差、数据处理整理和算法因素所产生的误差和海洋磁力测量实施过程中的误差。
4. 拖鱼位置归算误差(T1)
位置误差即磁力仪观测位置并非实际位置,而产生的误差。海洋磁力测量存在明显的动态性,受到风、流、涌等因素的影响测船定位。从而产生定位误差,本文将其称为位置误差的直接影响。而磁力测量中,为了减小船磁效应,海洋磁力仪通常采取拖曳式作业。这样,使得定位中心和磁测中心不一致,因此,海洋磁力测量数据处理时还必须对拖鱼的位置进行归算,本文将拖鱼位置归算时造成的误差称为位置误差的间接影响。
为了减小位置误差的影响,在施测过程中。应严格控制船速,使测船和拖鱼沿计划航线匀速、直线航行,当实际航线偏离计划航线较大时应该及时修正,以减小位置误差的影响。对于高精度的海洋磁力测量,还可以通过船姿传感器来藏小位置误差的直接影响。为了对拖鱼位置进行准确归算。在数据处理时,可先对测船的航迹线进行复原,即进行测线拟合。清除一些随机干扰的影响。按目前海上调查实施现状,如没有安装探头位置定位器来确定拖曳探头的具体位置,则通过调查船航向、船舷向和航速等记录数据来进行磁测探头的位置改正应是一种较为有效的解决方案。实际海洋磁测中,往往导航定位天线位置与磁测电缆固定位置不一致,这样就需要先利用简单改正推算电缆固定位置后,再结合航向、船舷向及航速等参数计算探头实际位置。同时由于海流的影响,船舷向在测量过程中是不断变化的,但其变化幅度一般不大,这样为简化计算并便于编程实现,可以考虑整条测线采用夹角 的平均值计算,对于较长的测线,或船舷向变化较大的情况,可以考虑分段平均的方法求取不同时段的夹角 平均值计算。合理有效地解决海洋磁测探头位置推算问题,将会提高磁测精度,同时也有利于进一步的磁测资料处理与解释工作。
5. 正常场校正误差(T2)
为了得到测点的磁异常,必须对磁测资料进行正常场校正。正常场校正值是由模拟地磁场时空分布与时间变化的正常场模型提供的。正常场模型有模拟全球地磁场分布的球谐模型,也有模拟区域地磁场分布的多项式模型、球冠模型和矩谐模型 [5]。采用不同的正常场模型提供的正常场校正值进行计算,结果是不一样的。由于我国海区还没进行过全面系统的地磁测量,因此,还没有适合模拟我田海区的地磁场正常场模型,早期的海洋磁力测量正常场校正使用中国科学院地球物理研究所提供的3阶泰勒多项式模型 [1]。其模型系数是由分布在我国大陆内的测量结果计算出来得出的。对于中国大陆的地区,其提供的正常场值较准确,而对于远离大陆的海区,则会存在很大的误差。因此,《规范》规定:海洋磁力测量地磁正常场计算采用国际地磁和高空物理协会(IAGA)提供的国际地磁参考场(IGRF) [3]。IGRF国际参考场模型是采用球谐分析的方法建立的,其可以模拟计算出全球任一点地球磁正常场值。IGRF正常场系数每五年更新一次,计算应选择最新的IGRF模型。相对于三阶多项式模型,在中国海区IGRF正常场模型可以提供更加准确的正常场校正值。
当选去IGRF模型作为正常场模型时,国际参考场模型在研究全球地磁场分布时效果较好,各国绘制的不同地区的地磁异常图便于比较。但是由于数据和计算能力的限制,它的分辨能力是有限的,不适宜处理某一地区地磁场或描述空间尺度较小的磁异常差异 [4]。在我国大部分地区,计算的地磁异常均为负异常,异磁场的分布不够均衡,忽略了区域性地壳磁异常的影响。现阶段我国海洋磁力测量地磁正常场校正采用国际高空物理和地磁协会最新的国际参考场模型,目前最新模型为IGRF2005.0-2010.0。
6. 地磁日变校正误差(T3)
地磁场是变化的磁场,地磁场随时闻的变化可分为长期变化和短期变化。由于海洋磁力测量的作业时间一般较短,因此影响海洋磁力测量的主要是短期变化,而短期变化影响中起主导作用的是太阳日变化。其变化量有时甚至可达40~60 nT [5]。因此,地磁日变改正是海洋磁力测量的一项重要工作。考虑到地磁日变的规律,为了消除其对测量的影响,通常在测区附近建立日变站,对测区的地磁日变规律进行观测和分析。测区范围较大时,可建立两个或几个日变站,但必须取其中一个作为整个测区地磁数据的起算零点:相邻两个日变站的控制范围要有重叠部分。以便根据重叠区同化两个日变站控制区的数据,并确定各个日变站相对总站的基值差。选取不同的日变改正方法,会产生不同的改正误差。
由于海水层对地磁日变的衰减作用,在一定水深范围内,地磁日变随着水深的增加而减小,但并非线性关系,在实际中应避免使用深水海底日变数据作地磁日变改正。D. R. Auld等比较沿岸日变站与测区纬度相差不大的海底日变站同步数据发现,经度相差7˚,地磁日变化的差异不超过3 nT [6] ;Riddihoug也发现纬度相近的两日变站,虽然经度差为4˚,地磁日变化差异不超过1 nT [7] ;邵关等人的研究表明,在400 m左右水深布设的海底日变站与陆地地磁台所测地磁日变曲线的形状、幅值、频率特征等非常相似,而且随着测区周围水深的增大,海底地磁日变数据的有效成分逐渐减少,存在明显的水层滤波作用 [8] ;夏伟等人给出了海面与海底地磁日变变化的计算公式,仿真分析了海面与海底地磁日变化差异 [9] ;边刚等采用不同的功率谱方法对地磁日变信号进行估计,采用功率谱估计用来分析地磁日变化的不同频率成分,并有效的压制随机噪声 [10] ;卞光浪等提出采用小波变换对日变信号进行多分辨率分解重构,可以剔除地磁日变信号中的噪声 [11]。这些研究的目的都在于提高日变改正的精度,减小日变校正的误差。
7. 船磁校正误差(T4)
测量船一般都是用强磁材料建造,因此在船体周围,除地磁场之外,还存在一个来源于船体的附加磁场,简称船磁。船磁对海洋磁力测量的影响是随着测船的航向、测船与拖鱼的距离和所处的磁场面变化的。不同测船在不同方位、不同距离以及不同测区,船磁的影响是不同的。为了有效地减小船磁效应,海上磁力测量时,一般将融力传感器探头拖曳于测量船之后一定距离(《规范》要求海洋磁力仪拖缆长度不得小于3倍船长。在开始测量前后,必须在测区进行船磁试验。船磁试验包括,船磁方位影响的试验和拖缆拖曳距离确定试验,获得必要的船磁改正方位曲线,确定拖缆最佳拖曳距离。
为了减小船磁校正误差,船磁方位测量应进行2或3次。航向误差不得大于10度 [12]。在数据处理时,可以探讨船磁改正的新方法。韩范畴等提出了傅立叶级数法计算船磁方位校正值,其是一种更优越的船磁改正法 [13]。
海洋磁力测量船大都是强磁性材料建造,强磁材料磁性一旦形成很难消失,这就是船磁的固有磁部分。同是,随测量船所处的地磁场变化以及测量船相对地磁场的空间方位变化,船磁也在不断地变化,这部分瞬时而变的附加磁场称为船磁的感应磁部分,因此测量船的此话磁场包括固有磁和感应磁两部分。
同时,传统船磁模型的常数项或改正基准的选取问题一直没有解决好,使得不同航磁、区块的测线数据存在很大的系统差,文章《海洋磁力测量中船磁方位改正的基准确定》注意到了这个问题,提出取垂直于地磁场方位且两两方向相反的多次测量平均值作为改正基准。而这个问题的根本在于传统船磁八方位实验测量中无法消除试验点的地磁异常。
8. 数据整理、处理过程产生的误差(T5):
海洋磁力测量资料处理过程中,必然会造成误差的出现,原始数据中的异常数据剔除不完整,异常数据超过所有数据的10%,测线编辑,整理不符合《海洋磁力测量要求》的规定,测点的位置计算不正确,不满足《海洋磁力测量要求》定位精度的规定,正常场模型选择不合理。测区范围较大时,未进行多台站日变改正,或多站日变改正机制归算方法不合理,日变改正值计算方法不得当,结果不准确。船磁校正值计算方法不合理,结果不准确。磁测总精度评价不合理,参加评价的起点书大于总交叉点数的3%,结果不符合《海洋磁力测量要求》精度的规定。数据网格化方法不合理,等值线勾绘较杂乱,土建整饰及绘制精度不符合《海洋磁力测量要求》的规定。等值线间隔应大于磁测精度10倍;地磁异常剖面图中正、负异常的面积分配不均匀。这些都是海洋磁力测量后期数据整理、处理过程中出现误差的方面。
9. 海洋磁力测量实施过程中的误差(T6)
海上磁测方法不合理,定位和磁测数据不同步,定位和磁测采样间隔大于10 s,数据记录较正确、连续,但不够完整;缺失数据的测线里程不超过测线里程的1%,并且每处超过5 km;主测线、检查线方向和测线间隔符合《海洋磁力测量要求》要求。测量过程中的船速和航空控制不够好,航速变化大于0.2 km,测线偏航距离保持在1/5 km。施测中拖鱼状态稳定,因拖鱼不稳定造成的漏测区域超过测线总里程的1% 。未对重点异常进行加密探测等对海洋磁力测量都会产生误差影响。
10. 误差评定
影响海洋磁力测量的误差是各项误差的综合,根据误差传播定律,
各项误差总影响可由(1)式表示:
(1)
T海洋磁力测量误差总影响;T0为由仪器产生的实时测量误差;T1为拖鱼位置误差;T2为正常场校正误差;T3为船磁校正误差;T4为日变校正误差;M为均方根误差;T5为数据整理、处理过程产生的误差;T6为海洋磁力测量实施过程中的误差。
利用主测线与检查测线上的交叉点的磁测不符值对海洋磁力测量精度进行评定,其公式为:
(2)
式中,
为交差点磁测不符值,N为主测线与检查线实际交叉点的总数。海洋磁力测量中,大部分较大的强磁异常区的交叉点不符值大,可以不参加精度评估,但弃点数不能超过总交点数的3%。
在《海洋调查规范·海洋地质地球物理调查》中海洋地磁测量误差分配与比例尺要求相关,不同的调查比例尺的测量准确度要求如表1 [3] :单位:nT。
海洋磁力测量准确度以主、联络测线相交点的测量值差的均方根值作为衡量依据(表2) [3] ,而交点处测量值的准确性受上述诸多因素的影响,所以均方根值差的平方T2与各种因素引起的总误差T2成正相关关系,如下(3)式:
(3)
由于数据整理、处理过程产生的误差和海洋磁力测量实施过程中的误差不随海洋磁力测量比例尺的改变而有较大的改变,在求极限时可以视为常数α。
由上表可推出:
1) 当比例尺为
时:
(4)
2) 当比例尺为
时:
(5)
3) 当比例尺为
和
时:
(6)

Table 1. Table of measurement accuracy ranges for different survey scales
表1. 不同的调查比例尺的测量精度范围表

Table 2. Table of measurement accuracy constraints for different survey scales
表2. 不同调查比例尺的测量精度约束范围表
当Ti取极大值时,不同海洋磁力测量比例尺误差分配情况如图1。
误差全定义域范围内平均分配,可得出关系如图2。
当Ti取中值时,不同海洋磁力测量比例尺误差分配情况如图3。
可得出关系如图4。
Ti在取中值与极大值时具有相似的折线走势,说明在海洋磁力测量中误差的取值具有相似的误差分配特点,在实际的海洋磁力测量过程中,各个误差的大小在中值与极大值之间,比较Ti取中值与极大值得折线统计图,具有一定的说服性。
11. 结论与建议
在实际的海洋磁力测量过程中,各个误差的大小在中值与极大值之间,比较Ti取中值与极大值得折线统计图,可以发现误差随着海洋磁力测量的精度具有一定的分配规律:
1) 不同的Ti取值却有相似的误差分布规律,在小比例尺
时,按照《规范》的准确度容忍度,实测仪器误差、拖鱼位置误差,日变校正误差的对总误差影响较大,正常场校正误差与船磁校正误
 (a)
(a)  (b)
(b) 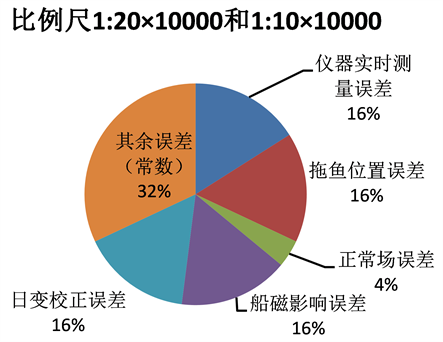 (c)
(c)
Figure 1. Ti takes the maximum value of the total error pie chart with different error ranges under different scales. (a) When Ti has a maximum scale of 1:100 × 104, the total error pie chart with different error ranges; (b) When Ti has a maximum scale of 1:50 × 104, the total error pie chart with different error ranges; (c) When Ti has a maximum scale of 1:20 × 104 and 1:10 × 104, the total error pie chart with different error ranges
图1. Ti取极大值不同比例尺下不同误差范围所占总体误差饼状图。(a) Ti取极大值比例尺为1:100 × 104时,不同误差范围所占总体误差饼状图;(b) Ti取极大值比例尺为1:50 × 104时,不同误差范围所占总体误差饼状图;(c) Ti取极大值比例尺为1:20 × 104和1:10 × 104时,不同误差范围所占总体误差饼状图
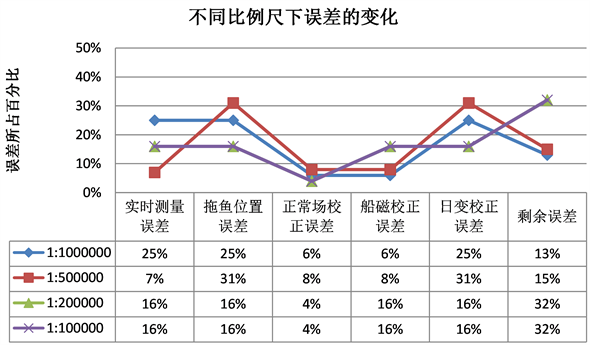
Figure 2. The change of error at different scales when Ti takes the maximum
图2. Ti取极大值时不同比例尺下误差的变化折线图
 (a)
(a) 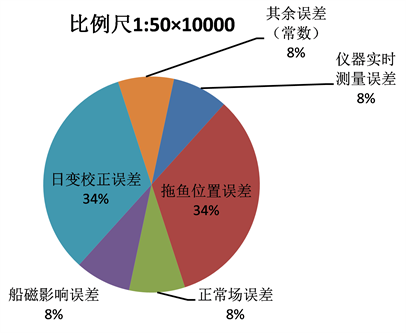 (b)
(b)  (c)
(c)
Figure 3. Ti takes the median value of the total error pie chart with different error ranges under different scales. (a) When Ti takes a median scale of 1:100 × 104, the total error pie chart with different error ranges; (b) When Ti takes a median scale of 1:50 × 104, the total error pie chart with different error ranges; (c) When Ti takes a median scale of 1:20 × 104 and 1:10 × 104, the total error pie chart with different error ranges
图3. Ti取中值时不同比例尺下不同误差范围所占总体误差饼状图。(a) Ti取中值比例尺为1:100 × 104时,不同误差范围所占总体误差饼状图;(b) Ti取极大值比例尺为1:50 × 104时,不同误差范围所占总体误差饼状图;(c) Ti取极大值比例尺为1:20 × 104和1:10 × 104时,不同误差范围所占总体误差饼状图
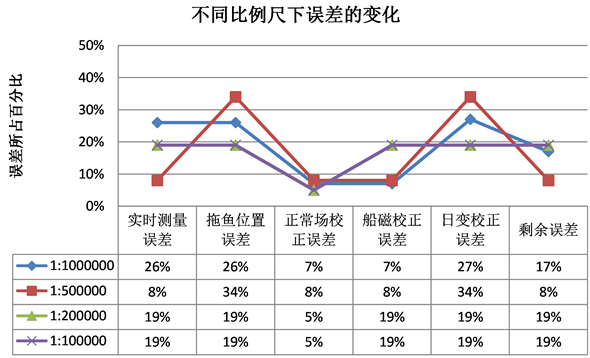
Figure 4. Change of error at different scales when Ti takes the median
图4. Ti取中值时不同比例尺下误差的变化折线图
差对总误差影响较小;数据整理、处理过程产生的误差和海洋磁力测量实施过程中的误差介于两者中间,在
比例尺时,拖鱼位置误差与日变校正误差为主要的误差来源,实时仪器测量误差、正常场校正误差和船磁校正误差相似且相对较小,数据处理整理误差和算法因素所产生的误差和海洋磁力测量实施过程中的误差略有增加,已经是不可忽视的误差影响;在
和
比例尺时,正常场误差所占比例最小,实测误差、拖鱼位置误差、船磁校正误差、和日变校正误差均等且在不同Ti取值时所占比例相似,而数据整理、处理过程产生的误差和海洋磁力测量实施过程中的误差在不同Ti取值时,所占比例有较大变化,随着Ti的取值的增大数据整理、处理过程产生的误差和海洋磁力测量实施过程中的误差所占比例增大,但任然是最主要的误差来源。
2) 随着比例尺的增大,实时测量误差即仪器误差的影响所占比例先缩小后变大,在实际海洋磁力测量过程中,要根据比例尺的实际情况做出相应的调整;拖鱼位置误差和日变校正误差基本一致,随着比例尺的增大,先增大后减小,并且在
时所占比例很大,建议在
度时,可以适当提高拖鱼位置和日变校正的准确度减小两者的误差,从而对减小总误差有明显的作用;正常场校正误差所占比例变化不大且较小;船磁校正误差随着比例尺精度增大而增大,在实际测量中随着精度要求的增大,要削弱船磁校正误差的影响;数据整理、处理过程产生的误差和海洋磁力测量实施过程中的误差在小比例尺测量时,影响程度不大,但是在大比例尺,海洋磁力测量精确度高的作业中,数据整理、处理过程产生的误差和海洋磁力测量实施过程中的误差成为主要误差。
3) 海洋磁力测量的误差是多项因素的综合误差,因此,对于其对海洋磁力测量的影响应综合考虑。本文建立了海洋磁力测量的数据误差处理模型,对影响海洋磁力测量的各项误差进行了分析,得出各误差在不同比例尺的海洋磁力测量中误差的变化规律,给出了海洋磁力测量误差分配方案,在确定海洋磁力测量的比例尺精确度要求后,一方面应该在测量实施时对各种误差的影响进行控制,另一方面应对海洋磁力测量的影响综合考虑,根据各项误差分配方案采取措施着重消除突出误差部分。
参考文献