1. 问题的研究背景
高效的校内超市与师生的学习、生活密不可分,但是校园超市由于得天独厚的地域优势,使得在校内具有一定的垄断地位,在缺乏竞争的环境下,校内超市缺乏改进和完善自身的动力,大多数学生对于校内超市提供的商品和服务存在不同程度的不满。在这种背景下,我们选择北区的教育超市作为研究对象,通过采访后勤集团与问卷相结合的方法,研究本校在校学生对校内超市的商品和服务的满意度以及影响满意度的因素,进而针对影响满意度的不同因素提出改进建议。本研究的研究成果对其他高校校内超市和其他商业性超市也有重要的借鉴意义。
2. 研究步骤
本次研究分为建立模型、确定指标、确定被测评对象、问卷设计、实施调查、数据汇总,统计检验、确定权重、计算顾客满意度、数据分析,制定对策九个步骤 [2] 。具体流程如下图1所示。
2.1. 建立模型
确定测评指标体系并进行量化。构建模型是进行顾客满意度测评的第一步,模型选择因行业、顾客群而异。现有文献中顾客满意度测评模型多数是基于ACSI模型建立起来的,本文也基于ACSI模型建立。
2.2. 确定指标
顾客满意度测评体系分为四大指标:总的测评目标“顾客满意度指数”为一级指标;顾客满意度指数模型中的六大要素:顾客期望、感知质量、感知价值、顾客满意度、顾客抱怨、顾客忠诚度,为二级指标;由二级指标具体展开而得到的指标,符合校园超市的特点,为三级指标;三级指标具体展开为问卷上的题项构成四级指标。
2.3. 确定被测评对象
由于本研究组所确定的研究对象为中国海洋大学崂山区北区教育超市,研究其顾客满意度,因此确定被测评对象为全体海大师生。
2.4. 问卷设计
问卷部分是顾客满意度测评指标体系中三级指标的具体延伸,具体化为校园超市的实际问题,是呈现给被测对象的最终材料。问卷要严格按照要求设计,尤其注意问题顺序与措辞准确性、可理解性,以保证最大程度挖掘到最真实的数据。
2.5. 实施调查
问卷的发放采用了网上电子问卷的形式,为收集到更多有效问卷,本小组通过中国海洋大学后勤集团官方公众号,中国海洋大学数学科学学院官方公众号对问卷进行发布,经过半个月的收集,得到了模型的数据。
2.6. 数据汇总,统计检验
调研者将问卷回收后,要统计出回收数量,剔除无效问卷的数量,计算问卷有效回收率,并对相应题项进行分类整理,然后对所收集数据进行信度和效度检验。信度是指服务业顾客满意度测评问卷中设置的指标反映顾客评价的可靠程度。估计可靠性的方法很多,不同的方法得到的结果说明的是可靠性的不同方面,本文采用Cornbach α系数检验可靠性。此外,为检验问卷设计的合理性,要对每一项测评指标对顾客评价结果的影响程度进行检验,同时,也要对问卷中测评指标的分类的合理性进行检验。一般采用因子分析法对以上两个方面进行合理性检验。经过统计检验,如果不符合统计规律,说明设计的测评指标体系不符合要求,需要返回第一步重新设计。
2.7. 确定权重
顾客满意度测评指标体系中包含了影响顾客满意的各级指标,但是每个指标并不是均衡的作用于顾客满意,因此,必须要确定出各级指标对顾客满意的贡献度(权重),否则,就会使得测评结果失真,无益于企业的质量管理工作。权重的确定是一个综合知识的调动,本文采用层次分析法和主成分分析综合的方法确定指标权重,尽量保证权重的客观公正性。
2.8. 计算顾客满意度
顾客满意度的计算比较简单,通过加权平均公式(1)就可实现,公式为:
(1)
式中CSD——顾客满意度;
——第i个指标的权重;
——第i个指标的评价;套用上述公式,可计算出企业内部某个部门或企业总体的顾客满意度。
2.9. 数据分析,制定对策
数据分析包括定性分析和定量分析。定性分析主要是对问卷中的问题的答案进行分析,首先了解顾客对企业满意程度的高低,其次,通过顾客对各个满意度指标的评价和重要程度,识别顾客满意的关键因素,初步总结出顾客满意或不满意的原因。量化分析可通过对数据进行简单描述性统计分析,发现样本的均值、方差等基本情况,然后利用SPSS统计软件技术对顾客满意的各指标数据的进一步分析,进而找出校园超市的薄弱环节,深入探究问题根源,并有针对性的制定改进策略。
3. 信度分析,效度分析
3.1. 信度分析
信度是指由若干个题目所构造的测试量表或问卷所测得的结果的稳定性和一致性,一般用信度系数来表示 [3] 。信度是判断问卷优劣的一个重要指标,通常信度系数越高,说明问卷或量表越科学合理,测试结果自然越可靠。Cornbach α系数是信度分析的常用方法之一 [4] 。
克朗巴哈系数(Cronbach’s alpha或Cronbach’s α)是一个统计量,是指量表所有可能的项目划分方法的得到的折半信度系数的平均值,是最常用的信度测量方法。它最先被美国教育学家Lee Cronbach在1951年命名。
若一份量表有n题,题间的平均相关系数为r,则此量表的标准化α系数为α = nr/[(n − 1)r + 1]。通常Cronbach α系数的值在0和1之间。如果α系数不超过0.6,一般认为内部一致信度不足;达到0.7~0.8时表示量表具有相当的信度,达0.8~0.9时说明量表信度非常好。Cronbach α系数的一个重要特性是它们值会随着量表项目的增加而增加,因此,Cronbach α系数可能由于量表中包含多余的测量项目而被人为地、不适当地提高。还有一种可以和Cronbach α系数同时使用的系数。系数能够帮助评价,在计算Cronbach α系数的过程中,平均数的计算是否掩盖了某些不相关的测量项目。不同的研究者对信度系数的界限值有不同的看法,有学者认为,在基础研究中Cronbach α系数至少应达到0.8才能接受,在探索研究中Cronbach α系数至少应达到0.7才能接受,而在实务研究中,Cronbach α系数只需达到0.6即可。
运用SPSS19.0进行信度检验,客户满意度问卷总的Cornbachα系数为0.823,见表1,大于0.8,表明整个量表的一致性很高。其他各二级指标的α系数也验证了量表的一致性是可以接受的,具体数据详见表2。
3.2. 效度分析
3.2.1. 内容效度
内容效度又称逻辑效度,是指项目对欲测的内容或行为范围取样的适当程度即测量内容的适当性和

Table 1. The total Cornbach α coefficient of questionnaires
表1. 问卷总的Cornbach α系数

Table 2. The Cornbach α coefficient of secondary indicators
表2. 各二级指标的Cronbsch α系数
相符性 [3] 。经过多次修改,本问卷在测评满意度以及语言表述方面得到顾客认可,可以认为本量表具有较好的内容效度。
3.2.2. 结构效度
因子分析是问卷、量表等社会科学领域内数据收集手段的结构效度分析的主要方法。结构效度是指问卷能够测量出某种理论特质或概念的程度,也就是实际的测量分数能够解释多少某一心理特质。结构效度的检验主要靠因子分析来检验问卷或量表的每一个结构对观测现象的整体方差的贡献大小。本研究主要对“超市各个方面的满意程度”的指标层次划分的合理性进行验证。在做因子分析之前都要进行巴特利特球形检验,用于判断变量是否适合用于做因子分析。巴特利特球形检验是以变量的相关系数矩阵为出发点的。当所有变量间的简单相关系数平方和远远大于偏相关系数平方和时,KMO值接近1。KMO值越接近于1,意味着变量间的相关性越强,原有变量越适合作因子分析;当所有变量间的简单相关系数平方和接近0时,KMO值接近0。KMO值越接近于0,意味着变量间的相关性越弱,原有变量越不适合作因子分析。由表3可看出KMO的值是大于0.813的,说明四级观测指标之间的偏相关度较高,因子分析的样本取样适合度比较高,显著性检验P值为0.000,达到极其显著的水平。两个检验结果都表明该量表适合做因子分析。
通过表4、表5的数据可以看出,测评指标体系中对于四级观测指标的降维是合理的,总共可划分为 2个因子,每个因子中涵盖了大于0.5 的各个不同数量的变量,2个因子总体解释了数据中69.625%的变异。
4. 模型的建立与求解
4.1. AHP模型构建及权重的确定
层次分析法是对一些较为复杂、较为模糊的问题做出决策的简易方法,它特别适用于那些难于完全定量分析的问题。是一种可以有效地将人的客观感知透过复杂的层次结构转化为重要系数的分析方法 [5] 。步骤如下。
4.1.1. 建立递阶层次结构模型
层次分析法方案层所对应问卷中的问题为:4,5,6,7;8,10,13,14,20,21;26;27,28 (其中26和28分别对应层次分析法中的两个指标)。根据本文指标结构,可构建如下图2所示的层次结构模型:

Table 3. The result of KMO measure and Bartlett test of sphercity
表3. KMO测度和巴特利特球体检验结果
4.1.2. 构造判断矩阵
设现要比较n个因子
对某因素Z的影响大小以
表示
和
对Z的影响大小之比,比较结果用矩阵
,称A为Z-X之间的成对比较判断矩阵。
一般为1~9及它们的倒数。具体数值与重要程度的关系如图3。
在本文中根据Delphi法,可构造二级指标对于超市满意度的判断矩阵如下式(2):
(2)
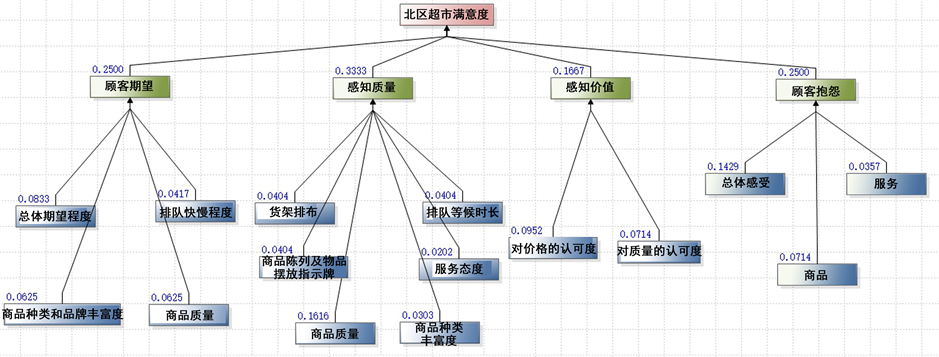
Figure 2. The model of analytic hierarchy process structure
图2. 层次分析结构模型

Figure 3. Judgment matrix and factors’ degree of importance
图3. 判断矩阵元素值与因子重要程度对应图
同理可构造三级指标对于顾客期望的判断矩阵,如下式(3):
(3)
构造三级指标对于感知质量的判断矩阵,如下式(4):
(4)
构造三级指标对于感知价值的判断矩阵,如下式(5):
(5)
构造三级指标对于顾客抱怨的判断矩阵,如下式(6):
(6)
4.1.3. 一致性检验
以 矩阵为例,计算其特征值为
和特征向量
如下:
(7)
计算一致性比例:
(8)
查表得:
(9)
代入数据得一致性比例:
(10)
通过一致性检验。
同理对其他判断矩阵进行一致性检验,均通过检验可以利用矩阵计算权重。输入判断矩阵,此处采用专家赋权法。得到如下标度(表6~表12),用图表进行显示。
4.1.4. 计算权重
根据判断矩阵计算各三级指标、二级指标的权重,并绘制成柱状图(图4)。
三级指标对于顾客期望的权重如图5所示。
三级指标对于感知质量的权重如图6所示。

Table 6. The rank and weight of factors in layer
表6. 方案层中要素对决策目标的排序权重

Table 7. The rank and weight of factors in the first middle layer
表7. 第1个中间层中要素对决策目标的排序权重

Table 8. The satisfaction of supermarket Consistency ratio: 0.0000; Weight: 1.0000; λ max :4.0000
表8. 北区超市满意度一致性比例:0.0000;对“北区超市满意度”的权重:1.0000;
:4.0000

Table 9. The expectation of customers Consistency ratio: 0.0000; Weight: 0.2500; λ max :4.0000
表9. 顾客期望一致性比例:0.0000;对“北区超市满意度”的权重:0.2500;
:4.0000

Table 10 . The perceived quality of customers Consistency ratio: 0.0000; Weight: 0.3333; λ max :6.0000
表10. 感知质量一致性比例:0.0000;对“北区超市满意度”的权重:0.3333;
:6.0000

Table 11 . The perceived value Consistency ratio: 0.0000; Weight: 0.1667; λ max :2.0000
表11. 感知价值一致性比例:0.0000;对“北区超市满意度”的权重:0.1667;
:2.0000

Table 12. The complain of customers Consistency ratio: 0.0000; Weight: 0.2500; λ max :3.0000
表12. 顾客抱怨一致性比例:0.0000;对“北区超市满意度”的权重:0.2500;
:3.0000

Figure 4. The weight of second degree factors to satisfaction of supermarket
图4. 各二级指标对于超市满意度的权重
三级指标对于感知价值的权重如图7所示。
三级指标对于顾客抱怨的权重如图8所示。
最终目标层各项指标的权重如下图9所示。
超市满意度=0.25顾客期望+0.33感知质量+0.17感知价值+0.25顾客抱怨。设
分别表示14个问题对应的满意度影响因素则可得各三级指标的权重,超市满意度为W,则有:
(11)
根据调查问卷获取各项得分取平均值后带入数据得:
(满分为5分)

Figure 5. The weight of third degree factors to the expectation of customers
图5. 三级指标对于顾客期望的权重
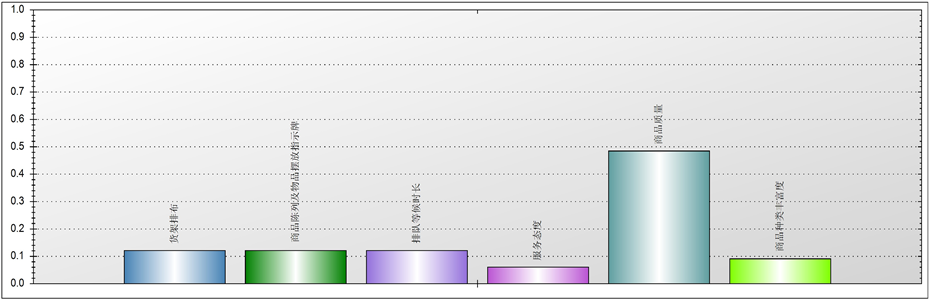
Figure 6. The weight of third degree factors to the perceived quality
图6. 三级指标对于感知质量的权重

Figure 7. The weight of third degree factors to the perceived value
图7. 三级指标对于感知价值的权重
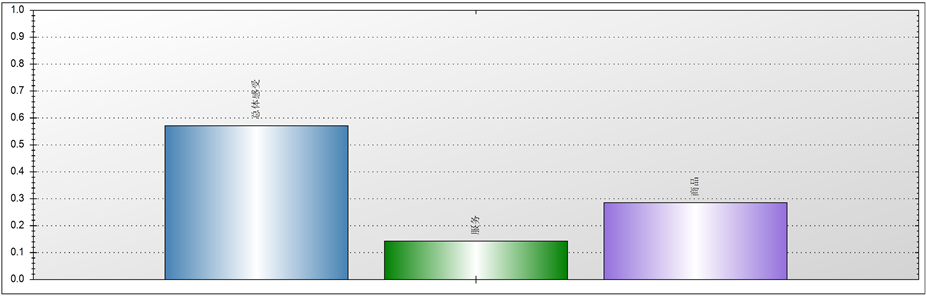
Figure 8. The weight of third degree factors to the complain of customers
图8. 三级指标对于顾客抱怨的权重
4.2. 主成分分析模型
为使结果更具有客观性,能更好地反映广大学子对北区超市的意见和建议。以给后勤集团提供更具有实质性的建议。本研究小组采用层次分析和主成分分析加权综合建模方法 [5] 。建立主成分分析模型如下。
4.2.1. 模型建立
由
分别表示13个问题对应的满意度影响因素,假设收到n份问卷。用
分别表示第i份问卷,第i份问卷的
的取值分别记作
,构造矩阵
。基于主成分分析的评价步骤如下。
1) 标准化处理
对原始数据进行标准化处理。将各消耗量
转化为标准化消耗指标
,有
#(12)
其中,
,
为第j个问题满意度的样本均值和样本标准差。
(13)
(14)
对应地,称:
#(15)
为标准化满意度指标变量。
2) 计算相关系数矩阵R
相关系数矩阵
,有
#(16)
式中:
;
,
为第i个指标与第j个指标的相关系数。
3) 计算特征值与特征向量
计算相关系数矩阵R的特征值
,及对应的标准化特征向量
,其中
,由特征向组成13个新的指标变量:
(17)
式中:
为第一主成分;
为第二主成分;……;
为第十三主成分。
4) 选择p个主成分,计算综合评价值
计算特征值
的信息贡献率和累积贡献率。称
#(18)
为主成分
的信息贡献率;而且称
#(19)
为主成分
的累积贡献率。当
接近于1
时,则选择前p个指标变量
作为p个主成分,代替原来13个指标变量,从而可以对p个主成分进行综合分析。
计算综合得分:
#(20)
式中:
为第j个主成分的信息贡献率,根据综合得分值就可进行评价。
4.2.2. 模型求解
利用MATLAB求得矩阵特征值及贡献率如表13。
可以看出前八个特征根的累计贡献率就达到85%以上,主成分分析效果很好。下面选取八个主成分进行综合评价。分别以八个主成分的贡献率为权重,构建主成分综合评价模型
(20)
把各个满意度影响因素的八个主成分值带入上式,可以得到各个满意度影响因素的综合评价结果,取平均值得到超市满意度的评价结果为3.27 (满分5分)。
5. 针对超市满足顾客需求的各方面的改进建议
5.1. 针对货架排布问题
调查结果如下,不满意的同学普遍觉得货架排布太紧密(图10)。
建议:
1) 由于文具类和洗漱类商品处人流较稀疏,而食品区尤其是酸奶区人流较密集,给人以紧密感。故应适当缩小文具类售卖区域的货架间距,节约空间给予食品区,实现更好地空间分布与利用。
2) 可以适当减少同种商品的摆放数量从而使货架排列变得稀疏。对于某些饮品的摆放(例如矿泉水),可以减少它们摆放在货架上的数量,由1排4列变为1排2列并采取多次进货的方法弥补数量上的减少。也可适当撤除一些货架,用增加补货次数和频率来实现商品的正常供应。
3) 可以选择在人流量较小的时候(如下午2:00~3:00,早晨9:00~11:00)进货,避开高峰期的同时又可以使商品数量得到满足,同时还可以使货架排列更稀疏。
4) 另外工作人员在超市内宣传新商品时也会占据一定的空间,为了避免拥堵,可以不用工作人员在超市内宣传商品,而改用超市的广播宣传新的商品。目前超市中放的音乐声音较小,特别是在高峰期时,超市内环境嘈杂,放音乐的效果并不明显,故可以将音乐改为播放宣传语以达到腾出空间,宣传商品的目的。

Table 13. The results of principal component analysis
表13. 主成分分析结果
5.2. 针对商品排布问题
调查结果如下,发现同学们主要问题针对在寻找商品上,而且普遍认为商品指示牌不明显(图11,图12)。
建议:
1) 更改指示牌排放位置,由目前的挂在天花板上改为立在货架上方。对于目前的方式,有些指示牌放置太高,离货架比较远,所以看起来不明显。所以需要降低高度,将指示牌放置在较低的位置(货架上方)。对于有些较为明显的产品(如牛奶、酸奶、饮料类等)也可以选择不设置指示牌以便节约空间,但是对于一些冷门商品(如特殊零食类)需要设立较为明显的指示牌。也可以选择增加地贴,指示同学们寻找商品时的方向。
2) 尽量将商品分类合理,将热门商品设置处分散开,避免过于集中造成拥挤。
5.3. 针对商品丰富度问题
对于丰富度的问题,同学们意见呈现多样化。建议超市合理利用意见簿,选取集中反映大部分人喜好的物品和品牌进货。调查结果如下(图13)。
5.4. 对于网红商品和现场加工零食的引入
经过调查发现,同学们对于网红商品并不是很高涨:超过一半(56.69%)的人对网红商品并不感兴趣。超市可以减少对于其宣传的力度以及其进货数量,以免出现滞销现象。66%的同学对小型现场加工类食

Figure 11. The findings of commodity arrangement (1)
图11. 商品排布调查结果(1)

Figure 12. The findings of commodity arrangement (2)
图12. 商品排布调查结果(2)
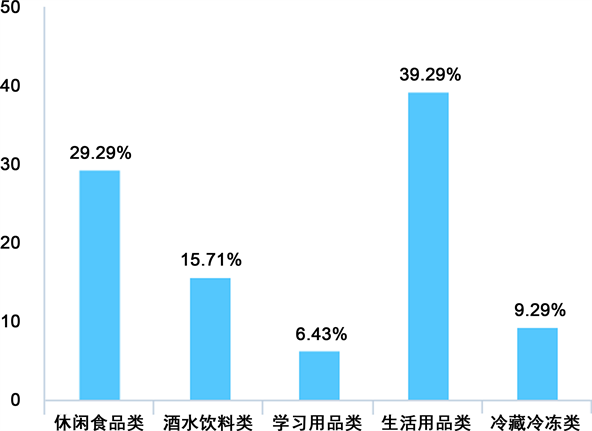
Figure 13. The findings of commodity abundance
图13. 商品丰富度调查结果
品(如关东煮)持不感兴趣或一般的态度。这种现场加工类食品如果放置在北海苑教育超市内,难免占用过多超市有限的面积,使货架排布,人群高峰期排队拥挤等问题更显著。设立与否还需要后勤集团更多考虑与权衡(图14)。
5.5. 对特定小型商品引进新的结账方式
建议:对纸巾、矿泉水、卷卷心、牛肉棒等生活用品、小零食等特定小型商品(目前有些摆放在收银台上,有些仍在超市里面)采用新的结账方式。例如可以在现有基础上设置一个新的专用收银台,只能用于特定小型商品的购买,可以有一个专门的工作人员,也可以把收银方式告诉大家,自助结账,但是如果没有人监督的话,可能会存在有个别同学不结账的风险。优点:减少排队人数,缩短排队时间,以此来提高顾客满意度。
5.6. 对会员卡引入方面
超过1/3的同学对会员卡较为期待,希望会员卡是以手机号等数字为识别模式。但考虑到所需的人力物力,还请超市慎重考虑。
致谢
在此特别感谢后勤集团给予的支持与资助,为海大后勤集团做些事,不仅仅可以及时反馈海大学子的心声与意见给后勤,有助于后勤集团推出相应政策和调整机制,更好地为广大师生服务,同时也会切实有助于提高后勤集团旗下北区超市的服务质量,为打造更先进,更高效,不断发展的新型高校超市贡献一份自己的力量,这想必是每个海大学子的荣耀。